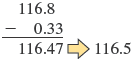Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019
Measurements and Calculations
Significant Figures
Objective
· To learn to determine the number of significant figures in a calculated result.
We have seen that any measurement involves an estimate and thus is uncertain to some extent. We signify the degree of certainty for a particular measurement by the number of significant figures we record.
Because doing chemistry requires many types of calculations, we must consider what happens when we do arithmetic with numbers that contain uncertainties. It is important that we know the degree of uncertainty in the final result. Although we will not discuss the process here, mathematicians have studied how uncertainty accumulates and have designed a set of rules to determine how many significant figures the result of a calculation should have. You should follow these rules whenever you carry out a calculation. The first thing we need to do is learn how to count the significant figures in a given number. To do this we use the following rules:
Rules for Counting Significant Figures
1. Nonzero integers. Nonzero integers always count as significant figures. For example, the number has four nonzero integers, all of which count as significant figures.
2. Zeros. There are three classes of zeros:
a. Leading zeros are zeros that precede all of the nonzero digits. They never count as significant figures. For example, in the number , the three zeros simply indicate the position of the decimal point. The number has only two significant figures, the and the .
b. Captive zeros are zeros that fall between nonzero digits. They always count as significant figures. For example, the number has four significant figures.
c. Trailing zeros are zeros at the right end of the number. They are significant only if the number is written with a decimal point. The number one hundred written as has only one significant figure, but written as ., it has three significant figures.
3. Exact numbers. Often calculations involve numbers that were not obtained using measuring devices but were determined by counting: experiments, apples, molecules. Such numbers are called exact numbers. They can be assumed to have an unlimited number of significant figures. Exact numbers can also arise from definitions. For example, inch is defined as exactly centimeters. Thus in the statement , neither nor limits the number of significant figures when it is used in a calculation.
Rules for counting significant figures also apply to numbers written in scientific notation. For example, the number . can also be written as , and both versions have three significant figures. Scientific notation offers two major advantages: the number of significant figures can be indicated easily, and fewer zeros are needed to write a very large or a very small number. For example, the number is much more conveniently represented as , and the number has two significant figures, written in either form.
Interactive Example 2.3. Counting Significant Figures
Give the number of significant figures for each of the following measurements.
a. A sample of orange juice contains g of vitamin C.
b. A forensic chemist in a crime lab weighs a single hair and records its mass as g.
c. The distance between two points was found to be ft.
d. In yesterday’s bicycle race, riders started, but only finished.
Solution
a. The number contains three significant figures. The zeros to the left of the are leading zeros and are not significant, but the remaining zero (a captive zero) is significant.
b. The number contains five significant figures. The leading zeros (to the left of the ) are not significant. The captive zeros between the and the are significant, and the trailing zero to the right of the is significant because the number contains a decimal point.
c. This number has four significant figures. Both zeros in are significant.
d. Both numbers are exact (they were obtained by counting the riders). Thus these numbers have an unlimited number of significant figures.
Self-Check: Exercise 2.2
· Give the number of significant figures for each of the following measurements.
a. m
b. L
c. Corvettes
See Problems 2.33 and 2.34.
Rounding Off Numbers
When you perform a calculation on your calculator, the number of digits displayed is usually greater than the number of significant figures that the result should possess. So you must “round off” the number (reduce it to fewer digits). The rules for rounding off follow.
Rules for Rounding Off
1. If the digit to be removed
a. is less than , the preceding digit stays the same. For example, rounds to .
b. is equal to or greater than , the preceding digit is increased by . For example, rounds to , and rounds to .
2. In a series of calculations, carry the extra digits through to the final result and then round off.* This means that you should carry all of the digits that show on your calculator until you arrive at the final number (the answer) and then round off, using the procedures in Rule 1.
We need to make one more point about rounding off to the correct number of significant figures. Suppose the number needs to be rounded to two significant figures. In doing this, we look only at the first number to the right of the :
The number is rounded to because is less than . It is incorrect to round sequentially. For example, do not round the to to give and then round the to to give .
When rounding off, use only the first number to the right of the last significant figure.
Determining Significant Figures in Calculations
Next we will learn how to determine the correct number of significant figures in the result of a calculation. To do this we will use the following rules.
Rules for Using Significant Figures in Calculations
1. For multiplication or division, the number of significant figures in the result is the same as that in the measurement with the smallest number of significant figures. We say this measurement is limiting because it limits the number of significant figures in the result. For example, consider this calculation:

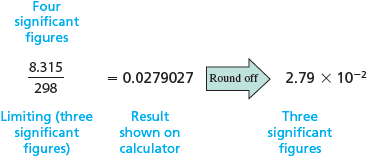
Because has only two significant figures, it limits the result to two significant figures. Thus the product is correctly written as , which has two significant figures. Consider another example. In the division , how many significant figures should appear in the answer?
Because has four significant figures, the number (with three significant figures) limits the result. The calculation is correctly represented as
2. For addition or subtraction, the limiting term is the one with the smallest number of decimal places. For example, consider the following sum:
Why is the answer limited by the term with the smallest number of decimal places? Recall that the last digit reported in a measurement is actually an uncertain number. Although , , and are treated as the same quantities by your calculator, they are different to a scientist. The problem above can be thought of as follows:
Because the term is reported only to the tenths place, our answer must be reported this way as well.
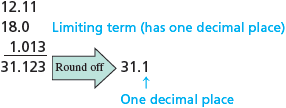
The correct result is (it is limited to one decimal place because has only one decimal place). Consider another example:
Note that for multiplication and division, significant figures are counted. For addition and subtraction, the decimal places are counted.
Now we will put together the things you have learned about significant figures by considering some mathematical operations in the following examples.
Interactive Example 2.4. Counting Significant Figures in Calculations
Without performing the calculations, tell how many significant figures each answer should contain.
a.
b.
c.
d. the total cost of boxes of candy at a box
Solution
a. The answer will have one digit after the decimal place. The limiting number is , which has one decimal place, so the answer has two significant figures.
b. The answer will have no digits after the decimal point. The number has no digits to the right of the decimal point and limits the result, so the answer has four significant figures.
c. The answer will have two significant figures because the number has only two significant figures ( has three).
d. The answer will have three significant figures. The limiting factor is because (boxes of candy) is an exact number.
Interactive Example 2.5. Calculations Using Significant Figures
Carry out the following mathematical operations, and give each result to the correct number of significant figures.
a.
b.
c.
d.
e.
Solution
· a.

The answer should contain three significant figures because each number being multiplied has three significant figures (Rule 1). The is rounded to because the following digit is greater than .
· b.

Because has the least number of significant figures (two), the result should have two significant figures (Rule 1).
· c.
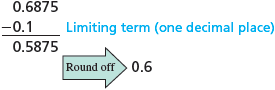
|
In this case is limiting (there are no digits after the decimal point). Thus the answer must have no digits after the decimal point, in accordance with the rule for addition (Rule 2). |
· d.
|
Because has only one decimal place, the answer must have only one decimal place (Rule 2). The is rounded up to because the digit to the right is greater than . Math Skill Builder When we multiply (or divide) and then add (or subtract) in a problem, we round the first answer from the first operation (in this case, multiplication) before performing the next operation (in this case, addition). We need to know the correct number of decimal places. |
· e.
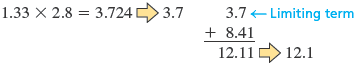
Note that in this case we multiplied and then rounded the result to the correct number of significant figures before we performed the addition so that we would know the correct number of decimal places.
Self-Check: Exercise 2.3
· Give the answer for each calculation to the correct number of significant figures.
a.
b.
c.
See Problems 2.47, 2.48, 2.49, 2.50, 2.51, and 2.52.