Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019

Measurements and Calculations
Problem Solving and Dimensional Analysis

Objective

· To learn how dimensional analysis can be used to solve various types of problems.

Suppose that the boss at the store where you work on weekends asks you to pick up dozen doughnuts on the way to work. However, you find that the doughnut shop sells by the doughnut. How many doughnuts do you need?

This “problem” is an example of something you encounter all the time: converting from one unit of measurement to another. Examples of this occur in cooking (The recipe calls for cups of cream, which is sold in pints. How many pints do I buy?), traveling (The purse costs pesos. How much is that in dollars?), sports (A recent Tour de France bicycle race was kilometers long. How many miles is that?), and many other areas.

How do we convert from one unit of measurement to another? Let’s explore this process by using the doughnut problem.

where ? represents a number you don’t know yet. The essential information you must have is the definition of a dozen:

You can use this information to make the needed conversion as follows:

You need to buy doughnuts.

Note two important things about this process.

1. The factor is a conversion factor based on the definition of the term dozen. This conversion factor is a ratio of the two parts of the definition of a dozen given above.

2. The unit “dozen” itself cancels.

Now let’s generalize a bit. To change from one unit to another, we will use a conversion factor.

The conversion factor is a ratio of the two parts of the statement that relates the two units. We will see this in more detail in the following discussion.

Earlier in this chapter we considered a pin that measured cm in length. What is the length of the pin in inches? We can represent this problem as

The question mark stands for the number we want to find. To solve this problem, we must know the relationship between inches and centimeters. In Table 2.7, which gives several equivalents between the English and metric systems, we find the relationship

This is called an equivalence statement . In other words, cm and in. stand for exactly the same distance (Fig. 2.1). The respective numbers are different because they refer to different scales (units) of distance.

Table 2.7. English—Metric and English—English Equivalents

The equivalence statement can lead to either of two conversion factors:

or

Note that these conversion factors are ratios of the two parts of the equivalence statement that relates the two units. Which of the two possible conversion factors do we need? Recall our problem:

That is, we want to convert from units of centimeters to inches:

We choose a conversion factor that cancels the units we want to discard and leaves the units we want in the result. Thus we do the conversion as follows:

Note two important facts about this conversion:

1. The centimeter units cancel to give inches for the result. This is exactly what we had wanted to accomplish. Using the other conversion factor would not work because the units would not cancel to give inches in the result.

As the units changed from centimeters to inches, the number changed from to . Thus cm has exactly the same value (is the same length) as in. Notice that in this conversion, the number decreased from to . This makes sense because the inch is a larger unit of length than the centimeter is. That is, it takes fewer inches to make the same length in centimeters.

The result in the foregoing conversion has three significant figures as required. Caution: Noting that the term appears in the conversion, you might think that because this number appears to have only one significant figure, the result should have only one significant figure. That is, the answer should be given as in. rather than in. However, in the equivalence statement , the is an exact number (by definition). In other words, exactly in. equals cm. Therefore, the does not limit the number of significant digits in the result.

We have seen how to convert from centimeters to inches. What about the reverse conversion? For example, if a pencil is in. long, what is its length in centimeters? In this case, the conversion we want to make is

What conversion factor do we need to make this conversion?

Remember that two conversion factors can be derived from each equivalence statement. In this case, the equivalence statement gives

or

Again, we choose which factor to use by looking at the direction of the required change. For us to change from inches to centimeters, the inches must cancel. Thus the factor

is used, and the conversion is done as follows:

Here the inch units cancel, leaving centimeters as required.

Note that in this conversion, the number increased (from to ). This makes sense because the centimeter is a smaller unit of length than the inch. That is, it takes more centimeters to make the same length in inches. Always take a moment to think about whether your answer makes sense. This will help you avoid errors.

Changing from one unit to another via conversion factors (based on the equivalence statements between the units) is often called dimensional analysis . We will use this method throughout our study of chemistry.

We can now state some general steps for doing conversions by dimensional analysis.

Converting from One Unit to Another

Step 1.

To convert from one unit to another, use the equivalence statement that relates the two units. The conversion factor needed is a ratio of the two parts of the equivalence statement.

Step 2.

Choose the appropriate conversion factor by looking at the direction of the required change (make sure the unwanted units cancel).

Step 3.

Multiply the quantity to be converted by the conversion factor to give the quantity with the desired units.

Step 4.

Check that you have the correct number of significant figures.

Step 5.

Ask whether your answer makes sense.

We will now illustrate this procedure in Example 2.6.

Interactive Example 2.6. Conversion Factors: One-Step Problems

An Italian bicycle has its frame size given as cm. What is the frame size in inches?

Solution

We can represent the problem as

In this problem we want to convert from centimeters to inches.

Step 1

To convert from centimeters to inches, we need the equivalence statement . This leads to two conversion factors:

and

Step 2

In this case, the direction we want is

so we need the conversion factor We know this is the one we want because using it will make the units of centimeters cancel, leaving units of inches.

Step 3

The conversion is carried out as follows:

Step 4

The result is limited to two significant figures by the number . The centimeters cancel, leaving inches as required.

Step 5

Note that the number decreased in this conversion. This makes sense; the inch is a larger unit of length than the centimeter.

Self-Check: Exercise 2.4

· Wine is often bottled in -L containers. Using the appropriate equivalence statement from Table 2.7, calculate the volume of such a wine bottle in quarts.

See Problems 2.59 and 2.60.

Next we will consider a conversion that requires several steps.

Interactive Example 2.7. Conversion Factors: Multiple-Step Problems

The length of the marathon race is approximately mi. What is this distance in kilometers?

Solution

The problem before us can be represented as follows:

We could accomplish this conversion in several different ways, but because Table 2.7 gives the equivalence statements and , we will proceed as follows:

This process will be carried out one conversion at a time to make sure everything is clear.

MILES → YARDS We convert from miles to yards using the conversion factor .

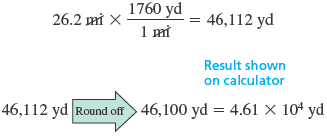
YARDS → METERS The conversion factor used to convert yards to meters is .

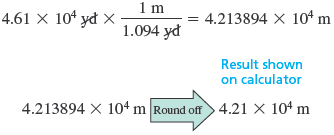
METERS → KILOMETERS Because , or , we convert from meters to kilometers as follows:

Thus the marathon ( mi) is km.

Once you feel comfortable with the conversion process, you can combine the steps. For the above conversion, the combined expression is

Note that the units cancel to give the required kilometers and that the result has three significant figures.

Self-Check: Exercise 2.5

· Racing cars at the Indianapolis Motor Speedway now routinely travel around the track at an average speed of mi/h. What is this speed in kilometers per hour?

See Problems 2.65 and 2.66.

Recap

Whenever you work problems, remember the following points:

1. Always include the units (a measurement always has two parts: a number and a unit).

2. Cancel units as you carry out the calculations.

3. Check that your final answer has the correct units. If it doesn’t, you have done something wrong.

4. Check that your final answer has the correct number of significant figures.

5. Think about whether your answer makes sense.