Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019
Chemical Composition
Calculation of Molecular Formulas
Objective
· To learn to calculate the molecular formula of a compound, given its empirical formula and molar mass.
If we know the composition of a compound in terms of the masses (or mass percentages) of the elements present, we can calculate the empirical formula but not the molecular formula. For reasons that will become clear as we consider Example 8.15, to obtain the molecular formula we must know the molar mass. In this section we will consider compounds where both the percent composition and the molar mass are known.
Interactive Example 8.15. Calculating Molecular Formulas
A white powder is analyzed and found to have an empirical formula of . The compound has a molar mass of g. What is the compound’s molecular formula?
Solution
Where Are We Going?
We want to determine the molecular formula for a compound. That is, we want to solve for and .
What Do We Know?
· The empirical formula of the compound is .
· The molar mass of the compound is g/mol.
· We know the atomic masses of phosphorus ( g/mol) and oxygen ( g/mol).
· The molecular formula contains a whole number of empirical formula units. So, the molecular formula will be .
What Do We Need to Know?
· We need to know the empirical formula mass.
How Do We Get There?
To obtain the molecular formula, we must compare the empirical formula mass to the molar mass. The empirical formula mass for is the mass of mole of units.
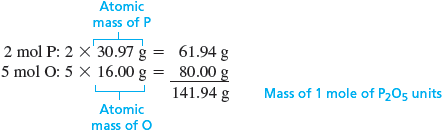
Recall that the molecular formula contains a whole number of empirical formula units. That is,
where is a small whole number. Now, because
then
Solving for gives
Thus, to determine the molecular formula, we first divide the molar mass by the empirical formula mass. This tells us how many empirical formula masses there are in one molar mass.
This result means that for this compound, so the molecular formula consists of two empirical formula units, and the molecular formula is , or . The structure of this interesting compound is shown in Fig. 8.5.
Figure 8.5.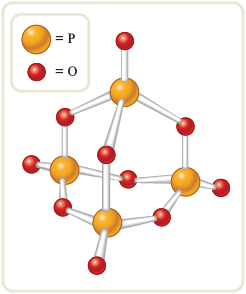
The structure of as a “ball-and-stick” model. This compound has a great affinity for water and is often used as a desiccant, or drying agent.
Reality Check The values for and are whole numbers. Also, the ratio of in the molecular formula is .
Self-Check: Exercise 8.11
· A compound used as an additive for gasoline to help prevent engine knock shows the following percent composition:
The molar mass is known to be g. Determine the empirical formula and the molecular formula for this compound.
See Problems 8.81 and 8.82.
It is important to realize that the molecular formula is always an integer multiple of the empirical formula. For example, the sugar glucose (Fig. 8.4) has the empirical formula and the molecular formula . In this case there are six empirical formula units in each glucose molecule:
In general, we can represent the molecular formula in terms of the empirical formula as follows:
where is an integer. If , the molecular formula is the same as the empirical formula. For example, for carbon dioxide the empirical formula and the molecular formula are the same, so . On the other hand, for tetraphosphorus decoxide the empirical formula is and the molecular formula is . In this case .