Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019

Chemical Composition
Calculation of Empirical Formulas

Objective

· To learn to calculate empirical formulas.

As we said in the previous section, one of the most important things we can learn about a new compound is its chemical formula. To calculate the empirical formula of a compound, we first determine the relative masses of the various elements that are present.

One way to do this is to measure the masses of elements that react to form the compound. For example, suppose we weigh out g of pure nickel metal into a crucible and heat this metal in the air so that the nickel can react with oxygen to form a nickel oxide compound. After the sample has cooled, we weigh it again and find its mass to be g. The gain in mass is due to the oxygen that reacts with the nickel to form the oxide. Therefore, the mass of oxygen present in the compound is the total mass of the product minus the mass of the nickel:

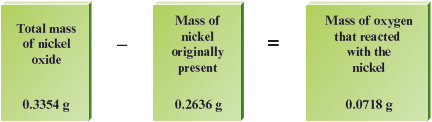
Note that the mass of nickel present in the compound is the nickel metal originally weighed out. So we know that the nickel oxide contains g of nickel and g of oxygen. What is the empirical formula of this compound?

To answer this question we must convert the masses to numbers of atoms, using atomic masses:

These mole quantities represent numbers of atoms (remember that a mole of atoms is atoms). It is clear from the moles of atoms that the compound contains an equal number of and atoms, so the formula is . This is the empirical formula; it expresses the smallest whole-number (integer) ratio of atoms:

That is, this compound contains equal numbers of nickel atoms and oxygen atoms. We say the ratio of nickel atoms to oxygen atoms is ( to ).

Interactive Example 8.11. Calculating Empirical Formulas

An oxide of aluminum is formed by the reaction of g of aluminum with g of oxygen. Calculate the empirical formula for this compound.

Solution

Where Are We Going?

We want to determine the empirical formula for the aluminum oxide, . That is, we want to solve for and .

What Do We Know?

· The compound contains g of aluminum and g of oxygen.

· We know the atomic masses of aluminum ( g/mol), and oxygen ( g/mol).

What Do We Need to Know?

· and represent moles of atoms in mole of the compound, so we need to determine the relative number of moles of and .

How Do We Get There?

We need to know the relative numbers of each type of atom to write the formula, so we must convert these masses to moles of atoms to get the empirical formula. We carry out the conversion by using the atomic masses of the elements.

Because chemical formulas use only whole numbers, we next find the integer (whole-number) ratio of the atoms. To do this we start by dividing both numbers by the smallest of the two. This converts the smallest number to .

Note that dividing both numbers of moles of atoms by the same number does not change the relative numbers of oxygen and aluminum atoms. That is,

Thus we know that the compound contains moles of atoms for every mole of atoms, or, in terms of individual atoms, we could say that the compound contains atoms for every atom. However, because only whole atoms combine to form compounds, we must find a set of whole numbers to express the empirical formula. When we multiply both and by , we get the integers we need.

Therefore, this compound contains two atoms for every three atoms, and the empirical formula is . Note that the ratio of atoms in this compound is given by each of the following fractions:

The smallest whole-number ratio corresponds to the subscripts of the empirical formula, .

Reality Check The values for and are whole numbers.

Sometimes the relative numbers of moles you get when you calculate an empirical formula will turn out to be nonintegers, as was the case in Example 8.11. When this happens, you must convert to the appropriate whole numbers. This is done by multiplying all the numbers by the same small integer, which can be found by trial and error. The multiplier needed is almost always between and . We will now summarize what we have learned about calculating empirical formulas.

Steps for Determining the Empirical Formula of a Compound

Step 1.

Obtain the mass of each element present (in grams).

Step 2.

Determine the number of moles of each type of atom present.

Step 3.

Divide the number of moles of each element by the smallest number of moles to convert the smallest number to . If all of the numbers so obtained are integers (whole numbers), these are the subscripts in the empirical formula. If one or more of these numbers are not integers, go on to step 4.

Step 4.

Multiply the numbers you derived in step 3 by the smallest integer that will convert all of them to whole numbers. This set of whole numbers represents the subscripts in the empirical formula.

Interactive Example 8.12. Calculating Empirical Formulas for Binary Compounds

When a -g sample of vanadium metal is heated in air, it reacts with oxygen to achieve a final mass of g. Calculate the empirical formula of this vanadium oxide.

Solution

Where Are We Going?

We want to determine the empirical formula for the vanadium oxide, . That is, we want to solve for and .

What Do We Know?

· The compound contains g of vanadium and has a total mass of g.

· We know the atomic masses of vanadium ( g/mol) and oxygen ( g/mol).

What Do We Need to Know?

· We need to know the mass of oxygen in the sample.

· and represent moles of atoms in mole of the compound, so we need to determine the relative number of moles of and .

How Do We Get There?

Step 1

All the vanadium that was originally present will be found in the final compound, so we can calculate the mass of oxygen that reacted by taking the following difference:

Step 2

Using the atomic masses ( for and for ), we obtain

Step 3

Then we divide both numbers of moles by the smaller, .

Because one of these numbers is not an integer, we go on to step 4.

Step 4

We note that and , so we multiply both numbers by to get integers.

This compound contains atoms for every atoms, and the empirical formula is .

Reality Check The values for and are whole numbers.

Self-Check: Exercise 8.8

· In a lab experiment it was observed that g of lead combines with g of chlorine to form a binary compound. Calculate the empirical formula of this compound.

See Problems 8.61, 8.63, 8.65, and 8.66.

The same procedures we have used for binary compounds also apply to compounds containing three or more elements, as Example 8.13 illustrates.

Interactive Example 8.13. Calculating Empirical Formulas for Compounds Containing Three or More Elements

A sample of lead arsenate, an insecticide used against the potato beetle, contains g of lead, g of hydrogen, g of arsenic, and g of oxygen. Calculate the empirical formula for lead arsenate.

Solution

Where Are We Going?

We want to determine the empirical formula for lead arsenate, . That is, we want to solve for , , , and .

What Do We Know?

· The compound contains g of , g of , g of , and g of .

· We know the atomic masses of lead ( g/mol), hydrogen ( g/mol), arsenic ( g/mol), and oxygen ( g/mol).

What Do We Need to Know?

· , , , and represent moles of atoms in mole of the compound, so we need to determine the relative number of moles of , , , and .

How Do We Get There?

Step 1

The compound contains g , g , g , and g .

Step 2

We use the atomic masses of the elements present to calculate the moles of each.

Step 3

Now we divide by the smallest number of moles.

The numbers of moles are all whole numbers, so the empirical formula is .

Reality Check The values for , , , and are whole numbers.

Self-Check: Exercise 8.9

· Sevin, the commercial name for an insecticide used to protect crops such as cotton, vegetables, and fruit, is made from carbamic acid. A chemist analyzing a sample of carbamic acid finds g of carbon, g of nitrogen, g of hydrogen, and g of oxygen. Determine the empirical formula for carbamic acid.

See Problems 8.57 and 8.59.

When a compound is analyzed to determine the relative amounts of the elements present, the results are usually given in terms of percentages by masses of the various elements. In Section 8.6 we learned to calculate the percent composition of a compound from its formula. Now we will do the opposite. Given the percent composition, we will calculate the empirical formula.

To understand this procedure, you must understand the meaning of percent. Remember that percent means parts of a given component per parts of the total mixture. For example, if a given compound is carbon (by mass), the compound contains g of carbon per g of compound.

Calculation of the empirical formula of a compound when one is given its percent composition is illustrated in Example 8.14.

Interactive Example 8.14. Calculating Empirical Formulas from Percent Composition

Cisplatin, the common name for a platinum compound that is used to treat cancerous tumors, has the composition (mass percent) platinum, nitrogen, hydrogen, and chlorine. Calculate the empirical formula for cisplatin.

Solution

Where Are We Going?

We want to determine the empirical formula for cisplatin, . That is, we want to solve for , , , and .

What Do We Know?

· The compound has the composition (mass percent) , , , and .

· We know the atomic masses of platinum ( g/mol), nitrogen ( g/mol), hydrogen ( g/mol), and chlorine ( g/mol).

What Do We Need to Know?

· , , , and represent moles of atoms in mole of the compound, so we need to determine the relative number of moles of , , , and .

· We have mass percent data, and to get to the number of moles we need to know the mass of each element (g) in the sample.

How Do We Get There?

Step 1

Determine how many grams of each element are present in g of compound. Cisplatin is platinum (by mass), which means there is g of platinum per g of compound. Similarly, a -g sample of cisplatin contains g of nitrogen , g of hydrogen , and g of chlorine .

If we have a -g sample of cisplatin, we have , g , g , and .

Step 2

Determine the number of moles of each type of atom. We use the atomic masses to calculate moles.

Step 3

Divide through by the smallest number of moles.

The empirical formula for cisplatin is . Note that the number for hydrogen is slightly greater than because of rounding-off effects.

Reality Check The values for , , , and are whole numbers.

Critical Thinking

· One part of the problem-solving strategy for empirical formula determination is to base the calculation on g of compound. What if you chose a mass other than g? Would this work? What if you chose to base the calculation on moles of compound? Would this work?

Self-Check: Exercise 8.10

· The most common form of nylon (Nylon-6) is carbon, nitrogen, hydrogen, and oxygen. Calculate the empirical formula for Nylon-6.

See Problems 8.67, 8.68, 8.69, 8.70, 8.71, 8.72, 8.73, and 8.74.

Note from Example 8.14 that once the percentages are converted to masses, this example is the same as earlier examples in which the masses were given directly.