Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019

Chemical Quantities
The Concept of Limiting Reactants

Objective

· To understand what is meant by the term “limiting reactant.”

Earlier in this chapter, we discussed making sandwiches. Recall that the sandwich-making process could be described as follows:

In our earlier discussion, we always purchased the ingredients in the correct ratios so that we used all the components, with nothing left over.

Now assume that you came to work one day and found the following quantities of ingredients:

· slices of bread

· slices of meat

· slices of cheese

How many sandwiches can you make? What will be left over?

To solve this problem, let’s see how many sandwiches we can make with each component.

Bread:

Meat:

Cheese:

How many sandwiches can you make? The answer is . When you run out of meat, you must stop making sandwiches. The meat is the limiting ingredient.

What do you have left over? Making sandwiches requires pieces of bread. You started with pieces, so you have pieces of bread left. You also used pieces of cheese for the sandwiches, so you have pieces of cheese left.

In this example, the ingredient present in the largest number (the meat) was actually the component that limited the number of sandwiches you could make. This situation arose because each sandwich required slices of meat—more than the quantity required of any other ingredient.

You probably have been dealing with limiting-reactant problems for most of your life. For example, suppose a lemonade recipe calls for cup of sugar for every lemons. You have lemons and cups of sugar. Which ingredient is limiting, the lemons or the sugar?*

A Closer Look

When molecules react with each other to form products, considerations very similar to those involved in making sandwiches arise. We can illustrate these ideas with the reaction of and to form :

Consider the following container of and :

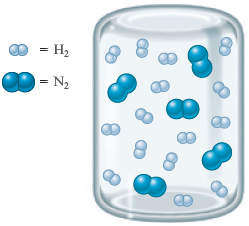
What will this container look like if the reaction between and proceeds to completion? To answer this question, you need to remember that each requires molecules to form . To make things more clear, we will circle groups of reactants:

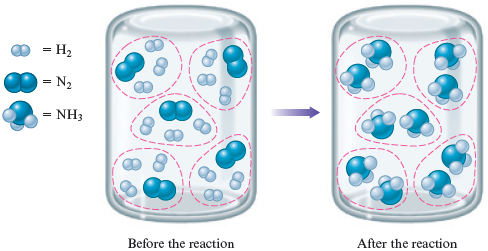
In this case, the mixture of and contained just the number of molecules needed to form with nothing left over. That is, the ratio of the number of molecules to molecules was

This ratio exactly matches the numbers in the balanced equation

This type of mixture is called a stoichiometric mixture—one that contains the relative amounts of reactants that match the numbers in the balanced equation. In this case, all reactants will be consumed to form products.

Now consider another container of and :

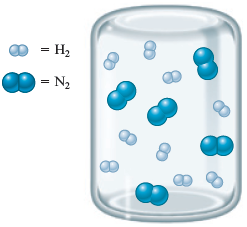
What will the container look like if the reaction between and proceeds to completion? Remember that each requires . Circling groups of reactants, we have

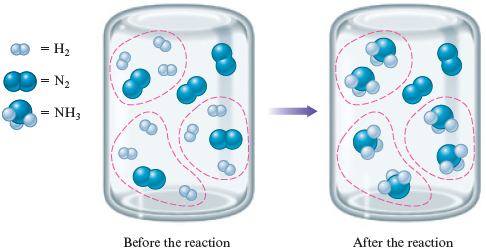
In this case, the hydrogen is limiting. That is, the molecules are used up before all of the molecules are consumed. In this situation, the amount of hydrogen limits the amount of product (ammonia) that can form—hydrogen is the limiting reactant. Some molecules are left over in this case because the reaction runs out of molecules first.

To determine how much product can be formed from a given mixture of reactants, we have to look for the reactant that is limiting—the one that runs out first and thus limits the amount of product that can form.

In some cases, the mixture of reactants might be stoichiometric—that is, all reactants run out at the same time. In general, however, you cannot assume that a given mixture of reactants is a stoichiometric mixture, so you must determine whether one of the reactants is limiting.

The reactant that runs out first and thus limits the amounts of products that can form is called the limiting reactant or limiting reagent .

Although this pictorial representation is a good visual to show us what is happening in the course of the reaction, we can also present this information in a table. To do so we must use the balanced chemical equation. Remember that the balanced equation tells us the relative numbers of molecules that react. The relative numbers of molecules mixed together are usually different from the coefficients in the balanced equation. In this case we are starting with molecules of and molecules of . These are numbers we use when trying to determine which reactant is limiting and how much product we form. We can organize our data as follows:

Note that the molecules of and molecules of (and no initially) are presented in the Before row. The Change row represents how much of each substance reacts or is produced. The After row represents how much of each substance remains in the final reaction mixture. We can tell from the pictorial representation which numbers belong in this table, but it is not always practical to do this, so let’s look at a general way to determine these numbers.

Because we are assuming that the reaction goes to completion, we know that at least one of the values for or must be zero in the After row. That is, we run out of at least one of the reactants. Thus, the two possibilities are:

Possibility I: runs out first

Possibility II: runs out first

For Possibility I we are assuming that we run out of , and for Possibility II we are assuming we run out of . How do we decide which of the possibilities is correct? We decide from our understanding of what a balanced chemical equation represents—the relative numbers of molecules that react. Recall that this is what the Change row represents as well. This brings us to a crucial idea: the ratio of the numbers in the Change row has to be the same as the ratio of the coefficients in the balanced equation. Let’s reconsider, then, the two possibilities with this in mind:

Possibility I: runs out first. so the change for must be :

How did we come up with these numbers? We know the numbers in blue because we were given the numbers in the Before row to reflect the original mixture. Because we are assuming that the runs out first, we have in the Change row. We determine the other two numbers in the Change row by using the ratio of the coefficients in the balanced equation. Because the ratio of the coefficients of to is , we can determine that the change for must be . That is, one-third as much is used as . The reactants are consumed, so the sign is negative. The ratio of the coefficients of to is , so we can determine the change for must be . That is, twice as much is produced as consumed.

We can use similar reasoning to complete the table for Possibility II:

Possibility II: runs out first, so the change for must be :

Now we can determine that the change for must be because three times as much is consumed as . Also, the change for must be (twice as much is formed as consumed).

We can see why is not limiting by looking at Possibility II. For all of the to react, we need more molecules of than we have. Because we cannot have a negative amount of a substance, Possibility II must not represent the reaction correctly.

Notice also that Possibility I conveys all of the information we initially saw in the picture of the reaction container. We begin with molecules of and molecules of , and after the reaction is complete, we are left with molecules of and molecules of .

Using a table such as this is convenient in that all of the information is conveyed: we now know which reactant runs out first, how much of the excess reactant is left over, and how much product is formed. It also emphasizes an understanding of what a balanced equation means because we have to use the ratio for the balanced equation in the Change row.

To this point, we have considered examples where the numbers of reactant molecules could be counted. In “real life” you can’t count the molecules directly—you can’t see them, and, even if you could, there would be far too many to count. Instead, you must count by weighing. We must therefore explore how to find the limiting reactant, given the masses of the reactants.