Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019

Chemical Quantities
Calculations Involving a Limiting Reactant

Objectives

· To learn to recognize the limiting reactant in a reaction.

· To learn to use the limiting reactant to do stoichiometric calculations.

Manufacturers of cars, bicycles, and appliances order parts in the same proportion as they are used in their products. For example, auto manufacturers order four times as many wheels as engines, and bicycle manufacturers order twice as many pedals as seats. Likewise, when chemicals are mixed together so that they can undergo a reaction, they are often mixed in stoichiometric quantities—that is, in exactly the correct amounts so that all reactants “run out” (are used up) at the same time. To clarify this concept, we will consider the production of hydrogen for use in the manufacture of ammonia. Ammonia, a very important fertilizer itself and a starting material for other fertilizers, is made by combining nitrogen from the air with hydrogen. The hydrogen for this process is produced by the reaction of methane with water according to the balanced equation

Let’s consider the question, What mass of water is required to react exactly with g of methane? That is, how much water will just use up all of the g of methane, leaving no methane or water remaining?

This problem requires the same strategies we developed in the previous section. Again, drawing a map of the problem is helpful.

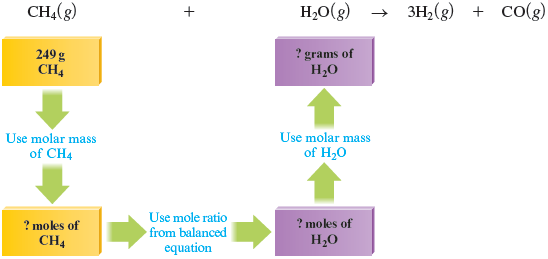
An equation shows methane (CH subscript 4) (g) and water (H subscript 2 O) (g) gives 3 diatomic molecules of hydrogen (H subscript 2) (g) and Carbon monoxide (CO) (g). An arrow (Use molar mass of CH subscript 4) points from “249 g CH subscript 4” to “question mark moles of CH subscript 4”, from where a second arrow (Use mole ratio from balanced equation) points to “question mark moles of H subscript O”, from where a third arrow (Use molar mass of H subscript 2 O) points to “question mark grams of H subscript 2 O.”

We first convert the mass of to moles, using the molar mass of ( g/mol).

Because in the balanced equation mole of reacts with mole of , we have

Therefore, moles of will react exactly with the given mass of . Converting moles of to grams of gives

This result means that if g of methane is mixed with g of water, both reactants will “run out” at the same time. The reactants have been mixed in stoichiometric quantities.

If, on the other hand, g of methane is mixed with g of water, the methane will be consumed before the water runs out. The water will be in excess. In this case, the quantity of products formed will be determined by the quantity of methane present. Once the methane is consumed, no more products can be formed, even though some water still remains. In this situation, the amount of methane limits the amount of products that can be formed. Recall from Section 9.4 that we call such a reactant the limiting reactant or the limiting reagent. There are two ways to determine the limiting reactant in a chemical reaction. One involves comparing the moles of reactants to see which runs out first. This concept is illustrated in Fig. 9.1. Note from this figure that because there are fewer water molecules than molecules, the water is consumed first. After the water molecules are gone, no more products can form. So in this case water is the limiting reactant.

Figure 9.1.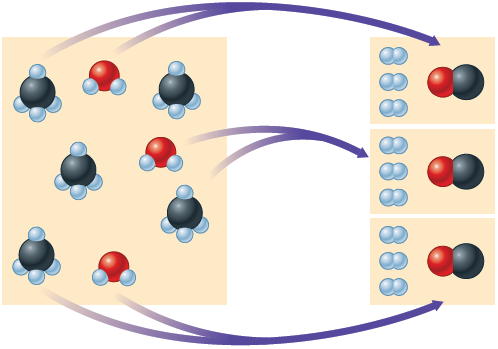An illustration shows molecular model of CH subscript 4 and H subscript 2 O mixture: three CH subscript 4 molecules react with H subscript 2 O to form three groups of 3H subscript 2 plus CO, leaving two CH subscript 4 unreacted.

A mixture of and molecules undergoes the reaction . Note that the molecules are used up first, leaving two molecules unreacted.

A second method for determining which reactant in a chemical reaction is limiting is to consider the amounts of products that can be formed by completely consuming each reactant. We can see this by considering our results when we reacted molecules of with molecules of to form :

Possibility I: runs out first




Before




Change




After




Possibility II: runs out first




Before




Change




After




Possibility I shows the amount of formed if is limiting, and Possibility II shows us the amount of formed if is limiting. Possibility I is correct because we cannot end up with a negative number of molecules. Notice that the amount of produced in Possibility I is less than that in Possibility II. This leads us to the general idea that the reactant that produces the smallest amount of product must run out first and thus be limiting. To see how this works when we are given masses, consider both approaches in Example 9.7.

Interactive Example 9.7. Stoichiometric Calculations: Identifying the Limiting Reactant

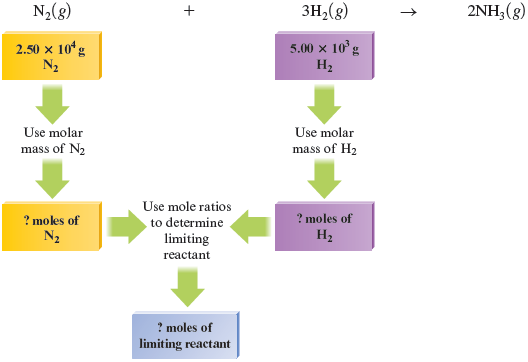
Suppose kg ( g) of nitrogen gas and kg ( g) of hydrogen gas are mixed and reacted to form ammonia. Calculate the mass of ammonia produced when this reaction is run to completion.

Solution

Where Are We Going?

We want to determine the mass of ammonia produced given the masses of both reactants.

What Do We Know?

· The names of the reactants and products.

· We start with g of nitrogen gas and g of hydrogen gas.

· We can obtain the atomic masses from the periodic table.

What Do We Need to Know?

· We need to know the balanced equation for the reaction, but we first have to write the formulas for the reactants and products.

· We need the molar masses of nitrogen gas, hydrogen gas, and ammonia.

· We need to determine the limiting reactant.

How Do We Get There?

The unbalanced equation for this reaction is

which leads to the balanced equation

This problem is different from the others we have done so far in that we are mixing specified amounts of two reactants together.

We first calculate the moles of the two reactants present:

· A.

First we will determine the limiting reactant by comparing the moles of reactants to see which is consumed first. That is, we must determine which is the limiting reactant in this experiment. To do so we must add a step to our normal procedure. We can map this process as follows:

An equation shows diatomic molecules of nitrogen (N subscript 2) (g) and 3 diatomic molecules of hydrogen (3 H subscript 2) (g) gives 2 moles of ammonia (2 NH subscript 3) (g). An arrow (Use molar mass of N subscript 2) points from “2.50 times 10 to the fourth power g N subscript 2” to “question mark moles of N subscript 2).” Two bifurcating arrows (Use mole ratios to determine limiting reactant) point from “question mark moles of N subscript 2” to “question mark moles of limiting reactant (branch)” and “question mark moles of H subscript 2.” Another arrow (Use molar mass of H subscript 2) points from “question mark moles of H subscript 2” to “5.00 times 10 to the third power g H subscript 2.”

We will use the moles of the limiting reactant to calculate the moles and then the grams of the product.

An equation shows diatomic molecules of nitrogen (N subscript 2) (g) and 3 diatomic molecules of hydrogen (3 H subscript 2) (g) gives 2 moles of ammonia (2 NH subscript 3) (g). An arrow (Use mole ratios involving limiting reactant) points from “moles of limiting reactant” to “moles of NH subscript 3”, from where a second arrow (use molar mass of NH subscript 3) points to “grams of NH subscript 3.”

Now we must determine which reactant is limiting (will be consumed first). We have moles of . Let’s determine how many moles of are required to react with this much . Because mole of reacts with moles of , the number of moles of we need to react completely with moles of is determined as follows:

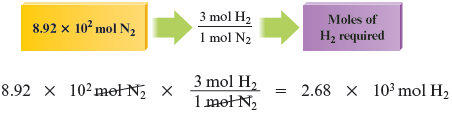
An arrow (3 mol H subscript 2 over 1 mol N subscript 2) points from “8.92 times 10 to the second power mol N subscript 2” to “moles of H subscript 2 required.” An equation reads 8.92 times 10 to the second power mol N subscript 2 times 3 mol H subscript 2 over 1 mol N subscript 2 equals 2.68 times 10 to the third power mol H subscript 2.

Is or the limiting reactant? The answer comes from the comparison

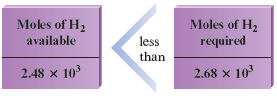
Moles of H subscript 2 available, 2.48 times 10 to the third power, is less than Moles of H subscript 2 required, 2.68 times 10 to the third power.

We see that moles of requires moles of to react completely. However, only moles of is present. This means that the hydrogen will be consumed before the nitrogen runs out, so hydrogen is the limiting reactant in this particular situation. Placing these numbers in a table as before, focusing on the Before and Change rows, confirms that there is not enough to react with all of the :




Before




Change




Note that in our effort to determine the limiting reactant, we could have started instead with the given amount of hydrogen and calculated the moles of nitrogen required.

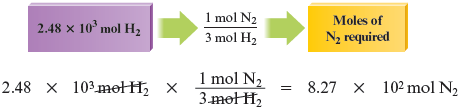
An arrow (1 mol N subscript 2 over 3 mol H subscript 2) points from “24.8 times 10 to the third power mol H subscript 2” to “moles of N subscript 2 required.” An equation reads 2.48 times 10 to the third power mol H subscript 2 times 1 mol N subscript 2 over 3 mol H subscript 2 equals 8.27 times 10 to the second power mol N subscript 2.

Thus moles of requires moles of . Because moles of is actually present, the nitrogen is in excess.

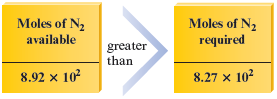
Moles of N subscript 2 available, 8.92 times 10 to the second power, is greater than Moles of N subscript 2 required, 8.27 times 10 to the second power.

If nitrogen is in excess, hydrogen will “run out” first; again we find that hydrogen limits the amount of ammonia formed.

Looking at these data in table form, once again focusing on the Before and Change rows, we see that does indeed limit the reaction:




Before




Change




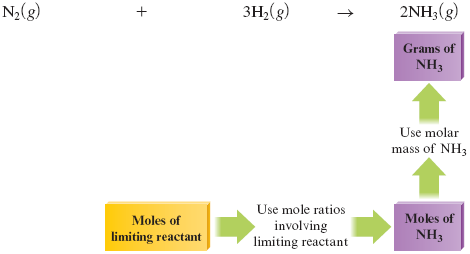
Because the moles of present are limiting, we must use this quantity to determine the moles of that can form.

· B.

Alternately we can determine the limiting reactant by computing the moles of that would be formed by the complete reaction of each and .

Because mole of produces moles of , the amount of that would be produced if all of the was used up is calculated as follows:

Next we calculate how much would be produced if the was completely used up:

Because a smaller amount of is produced from the than from the , the amount of must be limiting. Thus, because the is the limiting reactant, the amount of that can be produced is moles, as we determined before.

Next we convert moles of to mass of .

Therefore, kg of and kg of can form kg of .

Reality Check If neither reactant were limiting, we would expect an answer of kg of because mass is conserved . Because one of the reactants ( in this case) is limiting, the answer should be less than kg, which it is.

The strategies used in Example 9.7 are summarized in Fig. 9.2.

Figure 9.2.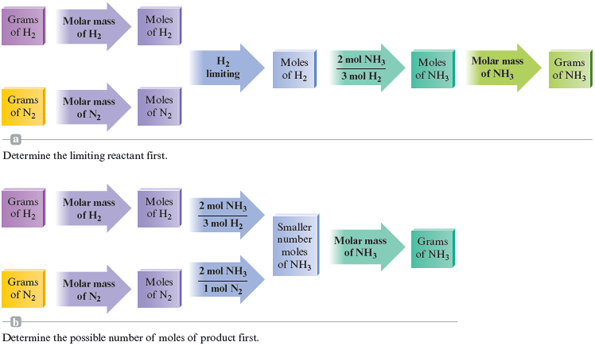An illustration shows a procedure map: An arrow, labeled Molar mass of H subscript 2 points, from “Grams of H subscript 2” to “Moles of H subscript 2”. The H subscript 2 limiting leads to “Moles of H subscript 2” and the ratio 2 mol NH subscript 3 / 3mol H subscript 2 giving “Moles of NH subscript 3”. The molar mass of NH subscript 3 turns moles of NH subscript 3 into grams of NH subscript 3. Another arrow (Molar mass of N subscript 2) points from “Grams of N subscript 2” to “Moles of N subscript 2.”

A map of the procedure used in Example 9.7.

The following list summarizes the steps to take in solving stoichiometry problems in which the amounts of two (or more) reactants are given.

Steps for Solving Stoichiometry Problems Involving Limiting Reactants

A screenshot show Steps for Solving Stoichiometry Problems Involving Limiting Reactants. Step 1: Write and balance the equation for the reaction. Step 2: Convert known masses of reactants to moles. Step 2 further leads to two steps One arrow from step 2 points toward the text reads, Step 3 Using the numbers of moles of reactants and the appropriate mole ratios, determine which reactant is limiting. Step 4 Using the amount of the limiting reactant and the appropriate mole ratio, compute the number of moles of the desired Another arrow from the step 2 points toward the text reads, Step 3 Using the appropriate mole ratios, compute the numbers of moles of product formed if each reactant were consumed. Step 4 Choose the least number of moles of product formed from Step 3. Arrows from both the step 4 points toward the text reads, Step 5 Convert from moles of product to grams of product, using the molar mass (if this is required by the problem).

Interactive Example 9.8. Stoichiometric Calculations: Reactions Involving the Masses of Two Reactants

Nitrogen gas can be prepared by passing gaseous ammonia over solid copper(II) oxide at high temperatures. The other products of the reaction are solid copper and water vapor. How many grams of are formed when g of is reacted with g of ?

Solution

Where Are We Going?

We want to determine the mass of nitrogen produced given the masses of both reactants.

What Do We Know?

· The names or formulas of the reactants and products.

· We start with g of and g of .

· We can obtain the atomic masses from the periodic table.

What Do We Need to Know?

· We need to know the balanced equation for the reaction, but we first have to write the formulas for the reactants and products.

· We need the molar masses of , and .

· We need to determine the limiting reactant.

How Do We Get There?

Step 1

From the description of the problem, we obtain the following balanced equation:

Step 2

Next, from the masses of reactants available we must compute the moles of and of .

· A.

First we will determine the limiting reactant by comparing the moles of reactants to see which one is consumed first. We can then determine the number of moles of formed.

Step 3

To determine which reactant is limiting, we use the mole ratio between and .

Then we compare how much we have with how much of it we need.

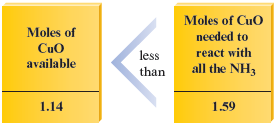
Moles of CuO available, 1.14 is less than Moles of CuO needed to react with all the ammonia (NH subscript 3), 1.59.

Therefore, moles of is required to react with moles of , but only moles of is actually present. So the amount of is limiting; will run out before does. We can also see this by placing the data in a table as before:



Products

Before




Change




As we can see, there is not enough to react with all of the , so is the limiting reactant.

Step 4

is the limiting reactant, so we must use the amount of in calculating the amount of formed. Using the mole ratio between and from the balanced equation, we have

· B.

Alternately we can determine the limiting reactant by computing the moles of that would be formed by complete combustion of and :

As before, is the limiting reactant, and we see that we produce mole of . Both methods lead us to the same final step.

Step 5

Using the molar mass of , we can now calculate the mass of produced.

Self-Check: Exercise 9.6

· Lithium nitride, an ionic compound containing the and ions, is prepared by the reaction of lithium metal and nitrogen gas. Calculate the mass of lithium nitride formed from g of nitrogen gas and g of lithium in the unbalanced reaction

See Problems 9.51, 9.53, and 9.54.