Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019
Chemical Quantities
Percent Yield
Objective
· To learn to calculate actual yield as a percentage of theoretical yield.
In the previous section we learned how to calculate the amount of products formed when specified amounts of reactants are mixed together. In doing these calculations, we used the fact that the amount of product is controlled by the limiting reactant. Products stop forming when one reactant runs out.
The amount of product calculated in this way is called the theoretical yield of that product. It is the amount of product predicted from the amounts of reactants used. For instance, in Example 9.8, g of nitrogen represents the theoretical yield. This is the maximum amount of nitrogen that can be produced from the quantities of reactants used. Actually, however, the amount of product predicted (the theoretical yield) is seldom obtained. One reason for this is the presence of side reactions (other reactions that consume one or more of the reactants or products).
The actual yield of product, which is the amount of product actually obtained, is often compared to the theoretical yield. This comparison, usually expressed as a percentage, is called the percent yield . Percent yield is important as an indicator of the efficiency of a particular reaction.
For example, if the reaction considered in Example 9.8 actually gave g of nitrogen instead of the predicted g, the percent yield of nitrogen would be
Interactive Example 9.9. Stoichiometric Calculations: Determining Percent Yield
In Section 9.1, we saw that methanol can be produced by the reaction between carbon monoxide and hydrogen. Let’s consider this process again. Suppose kg ( g) of is reacted with kg ( g) of .
a. Calculate the theoretical yield of methanol.
b. If g of is actually produced, what is the percent yield of methanol?
Solution (a)
Where Are We Going?
We want to determine the theoretical yield of methanol and the percent yield given an actual yield.
What Do We Know?
· From Section 9.1 we know the balanced equation is
· We start with g of and g of .
· We can obtain the atomic masses from the periodic table.
What Do We Need to Know?
· We need the molar masses of , , and .
· We need to determine the limiting reactant.
How Do We Get There?
Step 1
The balanced equation is
Step 2
Next we calculate the moles of reactants.
Step 3
Now we determine which reactant is limiting. Using the mole ratio between and from the balanced equation, we have
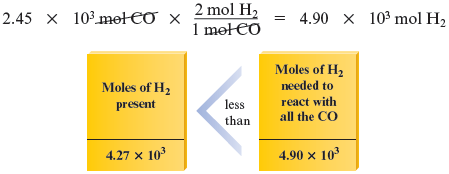
We see that moles of requires moles of . Because only moles of is actually present, is limiting.
Step 4
We must therefore use the amount of and the mole ratio between and to determine the maximum amount of methanol that can be produced in the reaction.
This represents the theoretical yield in moles.
Step 5
Using the molar mass of ( g), we can calculate the theoretical yield in grams.
So, from the amounts of reactants given, the maximum amount of that can be formed is g. This is the theoretical yield.
Solution (b)
The percent yield is
Self-Check: Exercise 9.7
· Titanium(IV) oxide is a white compound used as a coloring pigment. In fact, the pages in the books you read are white because of the presence of this compound in the paper. Solid titanium(IV) oxide can be prepared by reacting gaseous titanium(IV) chloride with oxygen gas. A second product of this reaction is chlorine gas.
a. Suppose g of titanium(IV) chloride is reacted with g of oxygen. Calculate the maximum mass of titanium(IV) oxide that can form.
b. If the percent yield of is , what mass is actually formed?
See Problems 9.63 and 9.64.