Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

3.5. The total Interaction

A comparison of the value of the various contributions to the van der Waals interactions is useful, and values as estimated for several small molecules are given in Table 3.1. Here, we limit ourselves to the Keesom, Debye and London contributions, since in many cases the interaction between neutral molecules is the most important, and three-body interactions are neglected anyway (see Section 3.7). The total Helmholtz interaction energy between two molecules is then

(3.18)

Table 3.1 The coefficient C₆(10⁻⁷⁹ J m⁶) in the vdW expression for several molecules at 300 K.^a)

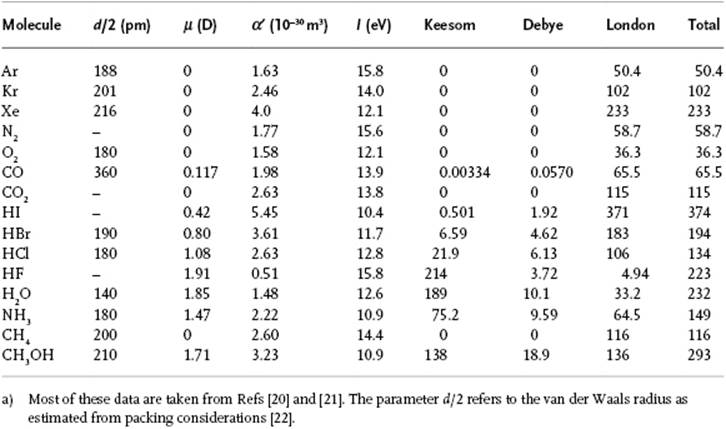
For this calculation we used the relatively simple model Drude model for the London interaction, with the characteristic energy estimated as the ionization potential I, implying that the estimate for the London interaction is approximate. From this comparison it becomes clear that in many cases the London dispersion interaction is dominating⁸⁾. Only for highly polar molecules does the Keesom interaction contribute significantly, for example, for H₂O and HF. As an aside, we note that incorporating higher-order terms into the analysis of the previous sections leads to ϕ_vdW = −C₆/r⁶ − C₈/r⁸ + … where the quantities C_i can all be expressed in terms of the moments of the charge distribution and polarizabilities of the molecules. We neglect these higher-order terms here.

In order to obtain the total interaction, we still need to add the repulsion acting at short distances between molecules. This interaction is due to orbital overlap, and hence is short-ranged and often called the Born repulsion. From quantum mechanics one can rationalize an exponential dependence, although in practice it is also often described by a power law. Hence we have

(3.19)

where (b,α) or (b,n) are parameters. The parameter n is typically in the range 10 to 12.

The total interaction energy is thus given by

(3.20)

Although the vdW interaction can be calculated with various degrees of sophistication, the repulsion is usually taken in to account as indicated above. In most cases the repulsion contributes significantly less than the attraction.

Problem 3.11

Calculate, using the value of C₆ between two Ar atoms and two HBr molecules (Table 3.1), the total interaction energy assuming that the molecules can be represented as attracting hard-spheres. Equating the result with kT, estimate the temperature for which dimer formation becomes significant.