Final Remarks - Lesson 4 - Some Special Topics: Surfaces of Liquids and Solutions - Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

Liquid-State Physical Chemistry: Fundamentals, Modeling, and Applications (2013)

15. Some Special Topics: Surfaces of Liquids and Solutions

15.7. Final Remarks

It seems that the eminent physicist Wolfgang Pauli used to say [50], “God made the bulk; surfaces were invented by the devil”, which was a succinct way of saying that surfaces are bestowed with many subtleties. In this chapter, we have only touched briefly on a few of these. In particular, the effects of curved and electrified surfaces were avoided, in spite of their obvious importance. For these aspects and other details we refer to the references in the section “Further Reading”. Even for those aspects that were touched, many more considerations can be made, just indicating the richness of the field, though further discussion of the various aspects of liquid surfaces is beyond the scope of the present text.

Notes

1) For a one-component system, such as a liquid–vapor system, usually addressed as surface tension.

2) The subscript xx refers to the force in the x-direction on a plane with normal in the x-direction, and is the standard notation for more complete discussions about mechanical stability. For full details see, e.g. Ref. [51].

3) Other definitions for the Gibbs energy of the interface exist because one can decide to transform with respect to all work terms, as in Eq. (15.9), or just using the volume work, i.e. using G′^(σ) ≡ F^(σ)+PV^(σ). The latter choice results in (deviating from the form for the bulk) and so that γ = (∂G′^(σ)/∂A)_T_,P,ni and (∂S^(σ)/∂A)_T_,P,ni = (∂γ/∂T)_A_,P,ni. In this case we have G = G^(α)+G^(β)+G′^(σ) (consistent with Eq. (15.3)), leading to the same result γ = (∂G/∂A)_T_,P,n.

4) The terms “surface tension,” “surface stress”, and “surface energy” are often used indiscriminately in the literature. Although not that important for liquids, it is still useful to make the distinction. Since all work is given by the product of a “generalized displacement,” for surface work the increase in area dA, and a “generalized force,” for surface work called surface stress Ψ, we have for a single-component, single-phase system δW = Ψ dA = d(γA). As all work terms in the Gibbs equation, Ψ is dependent on the conditions being kept constant. For example, at constant T and V, Ψ dA contributes to the Helmholtz energy. For liquid surfaces we have only a plastic increase of the surface area, that is, the average distance between molecules does not change upon increasing the area. For solid surfaces also an elastic increase of the surface area is possible, that is, the average distance between molecules does change upon increasing the area. Hence, in general the increase in area is given by dA = dA_ela + dA_pla. For a single-component, single-phase system we easily obtain:

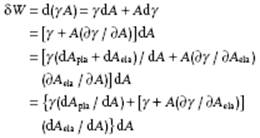
c15-math-5063

The above expression is conventionally designated as the Shuttleworth equation. For liquids, we regain the usual description δW = γ dA so that surface tension γ equals the surface stress Ψ, that is the force per unit length in the liquid that tends to contract and minimize the surface. For solids, the full term in square brackets describes the surface stress Ψ. In general, measuring Ψ for solids is a difficult task as different methods lead to different values for Ψand solid surfaces are usually not in equilibrium, as the relaxation might be kinetically hampered. Surface energy should refer to surface internal energy, similarly as energy refers to internal energy. Surface tension and surface Helmholtz energy have the same dimension and for liquids are numerically equal, as long as relaxation is fast. Note that surface internal energy has also the same dimension as surface tension but is not numerically equal. We use surface tension to avoid the somewhat longer surface Helmholtz energy and use, whenever required, the full designation.

5) Eötvös used K = 2.27 × 10⁻⁷ J K⁻¹ mol^−2/3, but the present value represents the state of affairs somewhat better. Slightly more precise estimates are obtained using the Eötvös–Ramsey–Shields rule , with K′ ≅ 2.12 × 10⁻⁷ J K⁻¹ mol^−2/3 and δ ≅ 6. There is no theoretical argument whatsoever for this modification [53].

6) Note that U^(σ) = γA where A is the molar area, which here is estimated with κ = 2^1/3.

7) A recent compilation of data [6c] yields for 85 normal liquids, r = 0.249 with a sample standard deviation of 0.054.

8) His paper has the inspiring title: How to get wrong results from good experimental data.

9) In fact, Riedel used a parameter α = 5.808 + 4.93ω, which is obviously fully equivalent to ω.

10) An interesting analogy exists between the gradient theory and classical mechanics (see Section 2.2). Denoting association with ↔, we have −F(ρ) ↔ potential energy Φ, m ↔ mass m, z ↔ time t and f(ρ)−μ₀ ↔ force F, so that Eq. (15.49) corresponds with Newton's law. The kinetic energy T ↔ ½mρ′(z)² and thus for the Lagrange function L = T − V ↔ ½mρ′(z)² + F(ρ), while for the total energy (Hamilton function) H = T + V ↔ ½mρ′(z)² − F(ρ) = 0. Minimizing γ as an integral over ½mρ′(z)² + F(ρ) corresponds with Hamilton's principle, which minimizes the action, that is, the integral over L.

11) This derivation also applies if we replace the concentration in the liquid phase c = N/V with P/kT (= N/V), where P is the pressure in the gas phase, representing the adsorption of a gas at the surface.

12) Often, is taken on the argument that the sites are localized but the molecules still vibrate with respect to the surface, leading to .

13) That is, use the zeroth order approximation for a regular solution model for the surface with w the average interaction energy per molecule (see Sections 8.3 and 15.5). Note that w < 0 since otherwise no attraction between the adsorbed molecules occurs.

14) The title of this paper is the rhetorical question: Should the Gibbs analysis be revised?

References

1 (a) Orowan, E. (1970) Proc. R. Soc., A316, 473; (b) Goodman, F.O. (1990) Surf. Sci. Lett., 232, 224.

2 Guggenheim, E.A. (1967) Thermodynamics, 5th edn, North-Holland, Amsterdam.

3 See Butt et al. (2006).

4 Eötvös, R. (1886) Ann. Phys., 263, 448.

5 Ferguson, A. (1916) Philos. Mag., 31, 37.

6 (a) Ferguson, A. (1923) Trans. Faraday Soc., 19, 407; (b) Ferguson, A. (1940) Proc. Phys. Soc. London, 52, 759; (c) Lin, H., Duan, Y.-Y., and Min, Q. (2007) Fluid Phase Eq., 254, 75.

7 Katayama, M. (1916) Rep. Tôhoku Univ., 4, 373.

8 Guggenheim, E.A. (1945) J. Chem. Phys., 13, 253.

9 McLeod, D.B. (1923) Trans. Faraday Soc., 19, 38.

10 (a) Sugden, S. (1924) J. Chem. Soc., 125, 32 and 1177; (b) Sugden, S. (1930) The Parachor and Valency, Routledge, London.

11 Quayle, O.R. (1953) Chem. Rev., 53, 439.

12 Poling, B.E., Prausnitz, J.M., and O'Connell, J.P. (2001) The Properties of Gases and Liquids, 5th edn, McGraw-Hill, London.

13 (a) Exner, O. (1962) Nature, 196, 890; (b) Exner, O. (1997) J. Phys. Org. Chem., 10, 797.

14 Riedel, L. (1954) Chem. Ing. Tech., 26, 679.

15 Pitzer, K.S. (1995) Thermodynamics, 3rd edn, McGraw-Hill, New York.

16 Davis, H.T. and Scriven, L.E. (1976) J. Phys. Chem., 80, 2805.

17 Egelstaff, P.A. and Widom, B. (1970) J. Chem. Phys., 53, 2667.

18 Bhatia, A.B. and March, N.H. (1978) J. Chem. Phys., 68, 19999.

19 Freeman, G.R. and March, N.H. (1998) J. Chem. Phys., 109, 10521.

20 Sanchez, I.C. (1983) J. Chem. Phys., 79, 405.

21 Kirkwood, J.G. and Buff, F.P. (1949) J. Chem. Phys., 17, 338.

22 Shoemaker, P.D., Paul, G.W., and Marc de Chazal, L.E. (1970) J. Chem. Phys., 52, 491.

23 Lekner, J. and Henderson, J.R. (1977) Mol. Phys., 34, 333.

24 Mulero, A., Galan, C., and Cuadros, F. (2003) J. Phys. Condens. Matter, 15, 2285.

25 Blokhuis, E.M. and Kuipers, J. (2006) J. Chem. Phys., 124, 074701.

26 (a) Toxvaerd, S. (1972) Progr. Surf. Sci., 3, 189; (b) Evans, R. (1979) Adv. Phys., 28, 143.

27 Penfold, J. (2001) Rep. Prog. Phys., 64, 777.

28 Widom, B. (1996) J. Phys. Chem., 100, 13190.

29 See Rowlinson and Widom (1982).

30 See Ted Davis (1995).

31 See Safran (1994).

32 See Hansen and McDonald (2006).

33 See Ted Davis and Scriven (1982).

34 Buff, F.P., Lovett, R.A., and Stillinger, F.H. Jr (1965) Phys. Rev. Lett., 15, 621.

35 (a) von Szyszkowski, B. (1908) Z. Phys. Chem., 64, 385; (b) Meissner, H.P. and Michaels, A.S. (1949) Ind. Eng. Chem., 41, 2782.

36 (a) Langmuir, I. (1917) J. Am. Chem. Soc., 39, 1848; this is the second paper of a series of three pioneering surface chemistry papers. The other two papers are: (b) Langmuir, I. (1916) J. Am. Chem. Soc., 38, 1848; and (c) Langmuir, I. (1918) J. Am. Chem. Soc., 40, 1361.

37 See Hiemenz and Rajagopalan (1997).

38 See Adamson and Gast (1997).

39 Laven, J. and de With, G. (2012) Langmuir, 27, 7958.

40 (a) Guggenheim, E.A. and Adam, N.K. (1933) Proc. Roy. Soc., A139, 218; (b) Guggenheim, E.A. (1967) Thermodynamics, 5th edn, North-Holland, Amsterdam.

41 (a) Surface tension data: Yano, Y.F. (2005) J. Colloid Interface Chem., 284, 255; (b) Surface structure via sum-frequency spectroscopy: Sung, J.S., Park, K., and Kim, D. (2005) J. Phys. Chem., B109, 18507.

42 Richmond, G.L. (2001) Annu. Rev. Phys. Chem., 52, 357.

43 (a) Penfold, J. and Thomas, R.K. (1990) J. Phys. Condens. Matter, 2, 1369; (b) Thomas, R.K. (2004) Annu. Rev. Phys. Chem., 55, 391.

44 Tarazona, P., Chaćon, E., and Bresme, F. (2012) J. Phys. Condens. Matter, 24, 284123.

45 (a) Wagner, C. (1924) Phys. Z., 25, 474; (b) Onsager, L. and Samaras, N.N.T. (1934) J. Chem. Phys., 2, 528; (c) Belton, J.W. (1937) Trans. Faraday Soc., 33, 1449.

46 Stairs, R.A. (1994) Can. J. Phys., 73, 781.

47 Schäfer, K.L., Pérez Masiá, A., and Jüntgen, H. (1955) Z. Elektrochem., 59, 425.

48 (a) Petersen, P.B. and Saykally, R.J. (2006) Annu. Rev. Phys. Chem., 57, 333; (b) Jungwirth, P. and Winter B. (2008) Annu. Rev. Phys. Chem., 59, 343.

49 (a) Jungwirth, P. and Tobias, D.J. (2001) J. Phys. Chem., B105, 10468; (b) Jungwirth, P. and Tobias, D.J. (2001) J. Phys. Chem., B105, 6361.

50 As quoted in Jamtveit, B. and Meakin, P. (1999) Growth, Dissolution, and Pattern Formation in Geosystems, Kluwer Academic Publishers, Dordrecht.

51 de With, G. (2006), Structure, Deformation, and Integrity of Materials, Wiley-VCH Verlag GmbH, Weinheim.

52 Moelwyn-Hughes, E.A. (1961) Physical Chemistry, 2nd edn, Pergamon, Oxford.

53 Ramsay, W. and Shields, J. (1893) Philos. Trans. A184, 647.

54 Curl, R.F. and Pitzer, K.S. (1958) Ind. Eng. Chem., 50, 265.