Organic Chemistry I For Dummies, 2nd Edition (2014)
Part IV. Spectroscopy and Structure Determination
Chapter 19. NMR Spectroscopy: Hold onto Your Hats, You’re Going Nuclear!
IN THIS CHAPTER
Discovering the power of NMR spectroscopy
Understanding chemical equivalency and symmetry
Examining an NMR spectrum
Combining integration and coupling
Seeing 13C NMR
Imagining modern organic chemistry without the aid of nuclear magnetic resonance (NMR) spectroscopy is a lot like imagining modern life without the aid of cellphones or toilet paper: virtually unthinkable. That’s because if one of the chief purposes of organic chemistry is to figure out ways to make carbon-containing stuff, then that process becomes a lot easier if you can determine what it is that you’ve made. And that’s what NMR is for — it can help you to determine the precise molecular structure of whatever organic stuff you’re interested in looking at. This stuff may include the products of reactions, an interesting metabolite that you’ve just isolated from rabbit muscle, a deadly neurotoxin that you’ve extracted from a marine shellfish, or just about anything else, really.
In this chapter, I explain the value of NMR, discuss how it works, and explain how NMR experiments are run. I also dissect the different pieces of an NMR spectrum, show you how all the different parts can give clues about a compound’s structure, and discuss what each part means. InChapter 20, I show you how to determine the structure of an unknown molecule using NMR spectroscopy.
Why NMR?
Back in the olden days when NMR spectroscopy was still in its infancy (and people had to walk 5 miles to get to school, uphill both ways), chemists had to labor sometimes for weeks to figure out the structures of even simple organic compounds, using methods that were tedious, time-consuming, and about as reliable as a fox guarding a hencoop. For example, a chemist might have compared the physical properties of a compound — its boiling point, melting point, refractive index, and so on — to compounds of similar structure previously reported in the literature to see if any of the known compounds were close matches. But because of the millions of possible structures, often the published literature contained no compounds of similar structure, so the molecule would need to be converted into a known derivative, and then the properties of this derivative would be tested.
Suffice it to say this method of structure determination was wearisome, unreliable, and about as fun as a root canal. But much to the delight of chemists today (and perhaps to the chagrin of the struggling organic student), NMR spectroscopy has now swaggered onto the scene. Hydrogen NMR can often be used to determine the structure of simple unknown compounds within minutes, eliminating most of the tiresome hassle figuring out the structures of molecules. You just pop your sample in the NMR spectrometer, run the experiment on the quick, and print out your data. Just like that — one, two, three — and you’re off to the analysis, as quickly as a politician to promise a tax cut.
Couple NMR’s speed with its ability to determine structure, and you’ve got a tool that’s amazingly powerful, a tool that can nail down the structure of almost any organic molecule, from the relatively small and simple molecules like the ones that you encounter in your organic course, to the large and staggeringly complex ones like the massive enzymes that catalyze chemical reactions in the cell. Because of NMR’s power and versatility, when organic chemists want to figure out exactly what that foul-smelling product from their reaction is, they turn to NMR to give them the definitive answer.
So, while mass spectrometry (see Chapter 17) can give you information about the molecular weight of a compound (and if you’re good, perhaps some of its structure), and IR spectroscopy (see Chapter 18) can give you an idea of what kinds of functional groups a molecule may have, only NMR can show you reliably how a molecule is pieced together. Don’t take this the wrong way: Mass spectrometry and IR spectroscopy are often integral pieces of structure determination, and they both provide first-class clues. But NMR is the Bad, Bad Leroy Brown of molecule identification. If figuring out a structure can be thought of as a chess game, then NMR spectroscopy has the moves of the queen: It’s the most powerful piece on the board.
How NMR Works
NMR spectroscopy works by allowing you to “see” the nuclei in a molecule, and to see the chemical neighborhood of those nuclei. Knowing the chemical environment and the number of different kinds of nuclei present allows you to piece together the structure of a compound in most circumstances. Some nuclei, however, are NMR active, and some are NMR inactive; NMR experiments see only NMR-active nuclei and are blind to nuclei that are NMR inactive. Fortunately, both carbon and hydrogen nuclei are NMR active. For reasons I talk about in this chapter, hydrogen NMR (often called proton NMR or 1H NMR) is often the most useful NMR type for organic chemists; therefore, all discussions will pertain to hydrogen NMR. After I cover hydrogen NMR, I cover the main points of 13C NMR (which is pretty much the same thing as hydrogen NMR, only simpler).
Giant magnets and molecules: NMR theory
The theory behind NMR spectroscopy can be complicated — and the details are generally outside the scope of a general organic class — so the following discussion is a simplified version of how NMR works. Even simplified, it’s complicated, so buckle up and fasten your thinking caps.
All nuclei with odd atomic and mass numbers have the property of spin just as electrons do, and any nucleus that has spin is observable by NMR. Spin is a bit of an abstract concept that doesn’t really have any counterpart outside of the subatomic world, but it might be helpful to think of these spins as coming from the protons spinning rapidly inside the nucleus, or the equivalent of a positive charge break dance. This spinning involves the movement of a positive charge, and, according to the laws of physics, the movement of charged particles creates a magnetic field with a magnetic moment. Nuclei that have such spins include 1H, 13C, 15N, and 19F, because all these elements have odd atomic numbers. Nuclei with even atomic numbers, like 16O, 12C, and 14N, are NMR inactive and will not show up in an NMR experiment.
The magnetic moments that come from the nuclear spins have direction. If you were to simply take a beaker full of nuclei and place it on a tabletop in your kitchen, the directions of the magnetic moments from the nuclei would be random, pointing in every possible direction. But when the nuclei are placed between the poles of a magnet — which creates what is called the external magnetic field — quantum mechanics dictates that the direction of the magnetic moments of these nuclei must either line up with the external magnetic field (called an α spin) or line up against it (called a β spin). You can imagine the magnet shouting a sort of politician’s rallying cry to the nuclei, “Everyone take sides; you’re either with me or you’re against me.” Thus, nuclei in the same beaker can line up with or against the external magnetic field (see Figure 19-1).
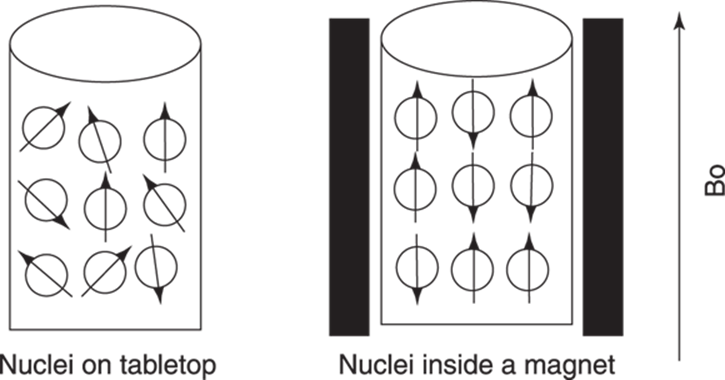
FIGURE 19-1: The effect of an external magnetic field on the direction of the magnetic moments of individual nuclei.
Those nuclei that align with the magnetic field are slightly lower in energy than those that align against the magnetic field. How much lower in energy these nuclei are depends on the size of the magnet that you put near the nuclei. (This magnet size — or external magnetic field strength — is often labeled Bo.) As the size of the magnet increases, the difference in energy (ΔE) between the spins aligning with the magnetic field (α) and those going against the magnetic field (β) also increases (see Figure 19-2). This energy gap between the two kinds of spins — α and β — is what an NMR experiment measures. In addition to the strength of the external magnetic field, the size of the energy gap is also affected by the chemical neighborhood of particular nuclei.
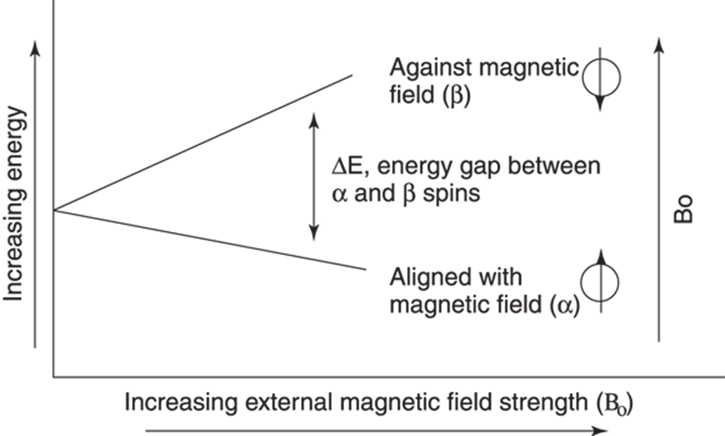
FIGURE 19-2: The effect of increasing external magnetic field strength (Bo) on the energy gap between α and β spin states.
But before I can talk about how the size of the energy gap between α and β spins gives you information about the chemical environment of the nuclei, I need to tell you how the energy gap is measured by an NMR spectrometer. Like most types of spectroscopy, NMR spectroscopy uses light to effect a transition between energy levels. (For IR spectroscopy, infrared light is used to transition between vibrational and rotational energy levels. See Chapter 18 for more on IR spectroscopy.) In an NMR experiment, a radio wave (which indicates light of radio frequencies) effects a transition between the α and the β spin energy levels. When the frequency of the radio wave that hits the sample has the exact energy of the energy gap between the α and β spins (ΔE), the light is absorbed by the nuclei.
The energy from the light absorption is used as a kind of nuclear spatula to flip the α spins into β spins, a process called spin flipping. When a nucleus absorbs light and flips its spin, the nucleus is said to be in resonance (which is where the term nuclear magnetic resonance comes from; this resonance is not to be confused with resonance structures). A detector can measure the frequency of this absorption and plot it on a spectrum (which is the plot of an NMR experiment, which shows the intensity of the light absorption versus the frequency of the light absorbed). SeeFigure 19-3 for a diagram of how this works. A high-frequency light absorption indicates a large energy gap between the α and β states; a low-frequency light absorption indicates a small energy gap.
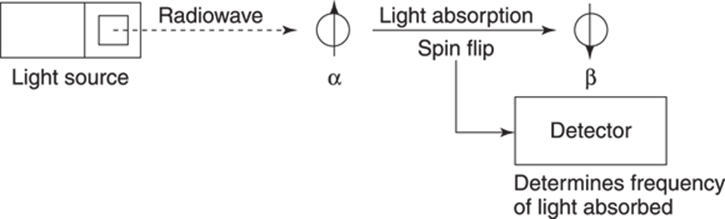
FIGURE 19-3: A diagram of the steps involved in measuring the ΔE in an NMR experiment.
To sum up, the ΔE in an NMR experiment is determined in the following way:
· The sample is placed inside a huge magnet (called the external magnetic field, or Bo).
· The direction of the magnetic moments of the nuclei line up either with the external magnetic field (an α spin) or against it (a β spin). The energy difference between an α spin and a β spin is the ΔE.
· Upon absorption of light that has energy equal to the energy gap (ΔE), the nuclei come into resonance, and α spins are flipped into β spins.
· A detector measures the frequency of the absorbed light (which is proportional to the energy gap between the α and β spins) and then plots the frequency of the light absorbed on the NMR spectrum versus the intensity of light absorption.
So, that’s how an NMR spectrometer determines the energy gap. But if all the hydrogen nuclei would have the same energy gap between α and β spins, the NMR spectrum would show only a single peak (or single light absorption), representing all the hydrogens in the molecule. And that wouldn’t be particularly helpful. But my discussion so far has omitted one key ingredient — electrons! So far, this discussion has been limited to bare nuclei that have no electrons surrounding them.
Grab your jackets: Electron shielding
Because they’re moving charges, electrons have their own magnetic fields that come into play. The magnetic field of an electron opposes the external magnetic field (made by the big magnet that you placed the sample into) and shields the nucleus from feeling the full brunt of the external magnetic field. In other words, a naked nucleus feels more of the external magnetic field than does a nucleus that has electrons surrounding it, just as a nudist will feel more of the cold than a person wearing an insulating jacket.
Consequently, a nucleus that is jacketed with electron density shielding it from the external magnetic field will require a lower frequency (lower energy) radio wave to flip its spin than a nucleus that has less electron density around it. This is because the actual magnetic field that an electron-surrounded nucleus feels is smaller than the magnetic field felt by a naked nucleus, so the gap between the α and β spins is smaller (refer to Figure 19-2). Because the gap is smaller, less energy (lower-frequency light) is required to flip the spin.
In this way, the chemical environment of the hydrogen nuclei is revealed. A hydrogen that’s next to a highly electronegative element (see Chapter 2 for a discussion of electronegativity) will have fewer electrons around it and will therefore come into resonance — or will flip its spin — at a higher frequency of light. A hydrogen that’s next to an electron-donating element will have lots of electrons around it and will come into resonance at a lower frequency.
The NMR Spectrum
An NMR spectrum, then, is the plot of the resonance frequency of the different nuclei versus intensity of light absorption. One way to take an NMR spectrum is to hold the external magnetic field constant (the magnetic field created by the big magnet) and vary the frequency of the radio waves irradiated onto the sample. At whatever frequencies light is absorbed, peaks are plotted on the spectrum. This is, in fact, how old NMR spectrometers plotted an NMR spectrum, and it’s a conceptually useful way of thinking about how an NMR spectrum is generated. The workings of a modern NMR spectrometer are a bit more complicated, but the general principle remains the same.
Standardizing chemical shifts
One potential problem for NMR is that if the nuclei are placed into a large magnet, their resonance frequency will be larger than when they’re placed into a little magnet, because the energy gap increases as the external magnetic field increases (refer to Figure 19-2). This means that a proton will show up at a different frequency for the poor person who can only afford a small magnet than it will for a rich person who can afford a big magnet. To make the NMR spectrum the same for a given molecule regardless of how large the magnet is, the resonance frequency is plotted relative to a reference compound, usually tetramethylsilane (TMS), shown in Figure 19-4. This way, regardless of how big the external magnetic field is, the peaks in the NMR spectrum will always occur at the same location relative to TMS.
FIGURE 19-4: Tetramethylsilane (TMS).
TMS is used as a reference because the hydrogens on the molecule are highly shielded because of the electron-donating silicon atom, and these hydrogens show up at a lower frequency than the vast majority of hydrogens in organic molecules. This TMS absorption frequency is arbitrarily assigned a value of zero on the spectrum. The frequency of a nucleus’s absorption relative to TMS is given in units of parts per million (ppm), so that the frequency will be given in small, manageable numbers (between 0 and 12) rather than large numbers (0 to 12 million). For a hydrogen NMR spectrum, peaks generally fall between 0 and 15 ppm, with a peak close to 0 ppm indicating a highly shielded hydrogen (electron rich), and a peak close to 15 ppm indicating a highly deshielded hydrogen (electron poor). Figure 19-5 shows a hypothetical NMR spectrum.

FIGURE 19-5: The NMR spectrum.
Seeing symmetry and chemical equivalency
Every hydrogen in a molecule that’s in a unique chemical neighborhood will show up as a peak on an NMR spectrum. Two (or more) hydrogens that have equivalent chemical neighborhoods, though, will be represented by just a single peak. Such hydrogens that are in identical chemical environments are said to be chemically equivalent. For example, methanol (see Figure 19-6) has four hydrogens in it, so you might expect it to show four peaks in the 1H NMR spectrum, one for each hydrogen. But it only shows two peaks. This is because there are only two different kinds of hydrogens in methanol. All the hydrogens in the methyl group (CH3) are in identical chemical environments — all three are attached to a carbon that’s bonded to two other hydrogens and an alcohol group — so each of these hydrogens sees the same chemical neighborhood. Therefore, all three hydrogens have the same resonance frequency and show up as a single peak. The second peak comes from the H on the alcohol (OH) group, which is in a different chemical environment.
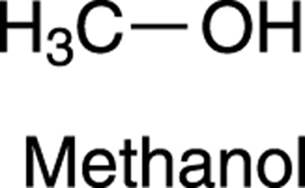
FIGURE 19-6: Methanol.
Butane (see Figure 19-7) is another example of a molecule that has such chemical equivalency. Ten hydrogens are on the molecule, but, remembering the chemical equivalency of methanol, you might expect to see four peaks, one for each of the hydrogen sets attached to the carbons. But the NMR spectrum of butane has only two peaks. This is accounted for by a further element of equivalency that comes from the symmetry of the molecule. Because the right-hand side of the molecule is exactly equal to the left-hand side, the two CH3 groups on the ends are in identical chemical environments, as are the two CH2 groups in the middle. Because both CH3 groups are in identical chemical environments, and both CH2 groups are in identical chemical environments, you see only two peaks in the NMR spectrum.
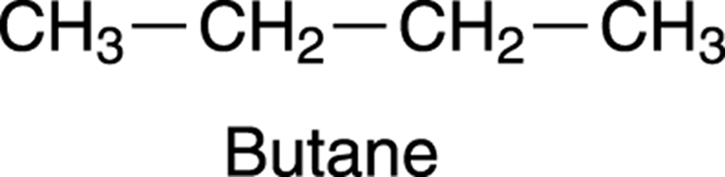
FIGURE 19-7: Butane.
Being able to recognize which hydrogens are chemically equivalent is extremely important. Generally, hydrogens attached to the same carbon are chemically equivalent. In addition, symmetry in the molecule can contribute further to chemical equivalency. You should practice looking at organic molecules for chemical equivalency so that you can determine how many peaks its 1H NMR will have (see the “Seeing the chemical shift” section, later in this chapter, for details).
 Often, drawing out all the hydrogens on the molecule can help you see the different chemical environments each hydrogen experiences. Try this for the molecules shown in Figure 19-8.
Often, drawing out all the hydrogens on the molecule can help you see the different chemical environments each hydrogen experiences. Try this for the molecules shown in Figure 19-8.
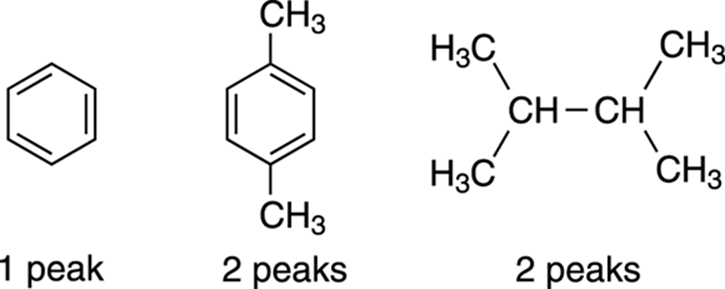
FIGURE 19-8: Seeing symmetry.
The NMR Spectrum Manual: Dissecting the Pieces
This section dissects each of the parts of an 1H NMR spectrum and discusses how each part of a spectrum can give clues to help determine the structure of a molecule.
Seeing the chemical shift
Where a peak is located relative to the reference TMS is called its chemical shift (or its δ value, where δ indicates the change in the absorption frequency). The chemical shift is given in units of parts per million (ppm). The two most important factors that affect the chemical shift of a given nucleus are the electron density around a hydrogen and diamagnetic anisotropy (scary phrase, huh?).
A hydrogen neighboring highly electronegative atoms — like fluorine (F), chlorine (Cl), bromine (Br), nitrogen (N), and oxygen (O) — will have a higher chemical shift than a hydrogen neighboring more electropositive elements (like silicon [Si] or carbon [C]). The derivatives of methane shown in Figure 19-9 illustrate this point. As the electronegativity of the substituent increases (recall that electronegativity increases as you go from Br to Cl to F), the chemical shift also increases. This is because as the electronegativity of the substituent increases, the electronpiggishness of the substituent also increases, and the substituent steals more of the electron density away from the hydrogens. Electron-deshielded nuclei like those near electronegative elements have a larger chemical shift than those near electropositive elements.
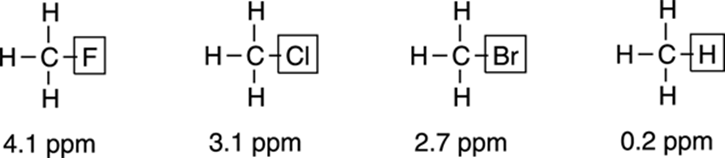
FIGURE 19-9: The chemical shifts of hydrogens (protons) caused by neighboring electronegative substituents.
The second effect on the chemical shift is a local field effect caused by pi electrons; this effect is called diamagnetic anisotropy in organic-speak.
When placed in a magnetic field, the pi electrons in benzene (or other aromatic rings) are induced to circulate. (For more on aromatic rings see Chapter 15. For information on pi bonds see Chapter 2.) This circulation of the pi electrons creates a local magnetic field from the aromatic ring (see Figure 19-10). In the center of the aromatic ring the induced magnetic field from the benzene opposes the external magnetic field, weakening it. Outside the ring, however, the magnetic field of the benzene ring reinforces the external magnetic field, making the magnetic field stronger.
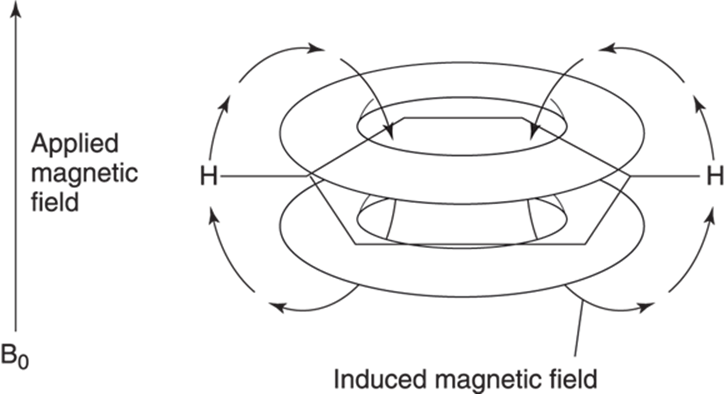
FIGURE 19-10: The induced magnetic field of benzene in an external magnetic field.
This means that any hydrogens near the center of an aromatic ring will be shielded by the aromatic ring’s magnetic field and will have a lower chemical shift, while those hydrogens outside the ring will be deshielded and will have a higher chemical shift. Therefore, hydrogens attached to aromatic rings (sometimes referred to as aromatic hydrogens, even though the hydrogens themselves are not aromatic) have a chemical shift much higher than you might expect based on the electronegativity considerations of the aromatic ring. Figure 19-11 illustrates this effect with a complex aromatic molecule.
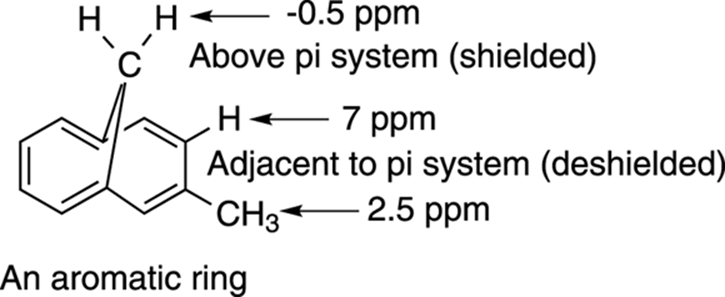
FIGURE 19-11: The effect of diamagnetic anisotropy in an aromatic molecule.
The same local field effect caused by the pi electrons in benzene affects double bonds and triple bonds in a similar fashion. Hydrogens attached to double bonds or triple bonds, therefore, have higher chemical shifts than might be expected based on simple electronegativity considerations.
Figure 19-12 shows some of the approximate chemical shifts of hydrogens adjacent to the common functional groups. Keep in mind, though, that these numbers are just typical ranges and are not absolute; values may stray in and out of the ranges depending on the rest of the structure of a given molecule. Also keep in mind that the addition of electronegative elements is cumulative. A hydrogen adjacent to a carbonyl group plus a halide would have a chemical shift higher than a hydrogen neighboring just one of those groups.
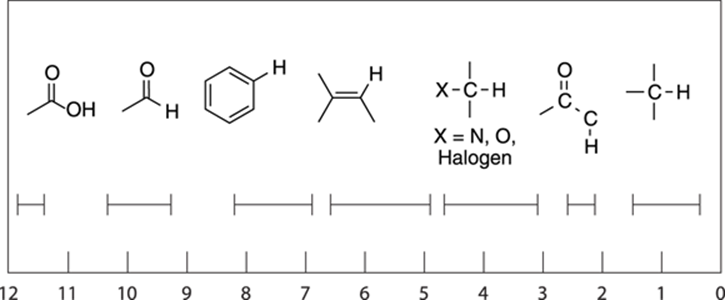
FIGURE 19-12: Approximate chemical shifts of hydrogens (protons) adjacent to the common functional groups.
Incorporating the integration
The peak intensity — or the area underneath a peak on a spectrum — is related to the number of hydrogens that the peak represents. A computer uses the mathematical process of integration to find the areas underneath each peak. Traditionally, integration is shown on the spectrum by the addition of an integration curve (see Figure 19-13), although modern computing has made digital integration common that doesn’t require you to do any measuring. The height of this integration curve is proportional to the area underneath a peak, so this height is proportional to the number of hydrogens the peak represents. (The width of the curve is unimportant.)
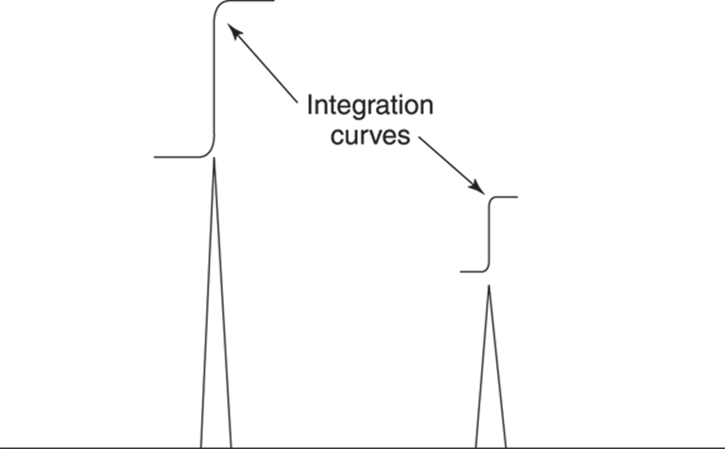
FIGURE 19-13: Integration curves and hydrogen peaks on an 1H NMR spectrum.
To measure the height of an integration, you start at the bottom of the integration curve where it’s flat, and measure to where the curve goes flat again. Unfortunately, integration can’t tell you how many hydrogens each peak represents — it just tells you the relative ratios of hydrogens in one type of chemical environment compared to those in another environment. This makes integration useful only for organic molecules that contain more than one kind of hydrogen (which, fortunately, is most of them).
For example, if there are two peaks, one with an integration curve that’s 2 cm high and one with an integration curve that’s 1 cm high, this tells you that the larger peak represents twice as many hydrogens as the smaller one (refer to Figure 19-13). This does not mean that the larger one represents two hydrogens and the smaller represents one hydrogen, necessarily — although this could be the case. It simply tells you that the ratio of hydrogens in the two chemical environments is 2:1. I show you how to measure an integration with a ruler in Figure 19-14.

FIGURE 19-14: How to measure the height of integration curves.
Catching on to coupling
Ethanol, the alcohol found in adult beverages, is a common organic compound. The NMR spectrum for ethanol is shown in Figure 19-15.
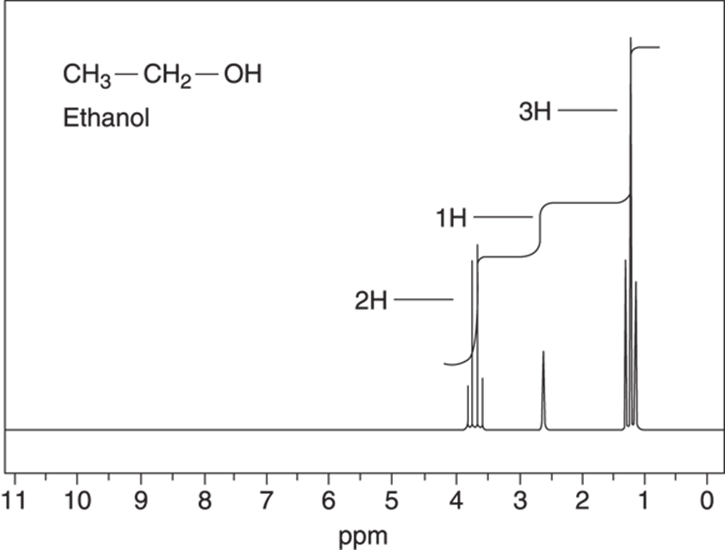
FIGURE 19-15: The NMR spectrum of ethanol, with the ratios of hydrogens shown beside the integration curves.
Ethanol has three kinds of hydrogens that are in unique chemical environments — the three hydrogens on the methyl group (CH3), the two hydrogens on the methylene group (CH2), and the hydrogen on the alcohol group (OH). That’s why you see three peaks in the NMR spectrum and why the integration has a ratio of 2:1:3, representing the methylene group, the alcohol group, and the methyl group hydrogens, respectively. Notice, though, that some of the individual absorptions are split further into smaller peaks. This is called coupling. Coupling is a phenomenon that’s useful in determining how each piece of the molecule is connected to the others. If integration tells you about the number of hydrogens a peak represents, coupling tells you how many hydrogens live next door to that hydrogen. Coupling comes from the interaction of the magnetic moments of the hydrogens with the magnetic moments of the neighboring hydrogens. In most cases, hydrogens only couple the hydrogens that are on adjacent carbons. Chemically equivalent hydrogens don’t couple, which is why hydrogens on the same carbon don’t couple most of the time and why the six hydrogens in benzene don’t couple.
The “n + 1 rule” and the coupling constant
Coupling follows what is called the n + 1 rule. This rule says that a peak will be split n + 1 times, where n is the number of equivalent neighboring hydrogens. In the spectrum for ethanol (refer to Figure 19-15), for example, the methyl (CH3) group has as its neighbor a carbon that has two equivalent hydrogens, so the methyl group signal is split into three peaks following the n + 1 rule (observed by the signal at δ1.2 ppm). The methylene group (CH2) is next to three equivalent hydrogens on the adjacent methyl group, so its signal is split into four peaks following the n+ 1 rule (see Figure 19-16). The hydrogen on the alcohol group doesn’t couple, for reasons I talk about in the subsequent section on proton exchange.
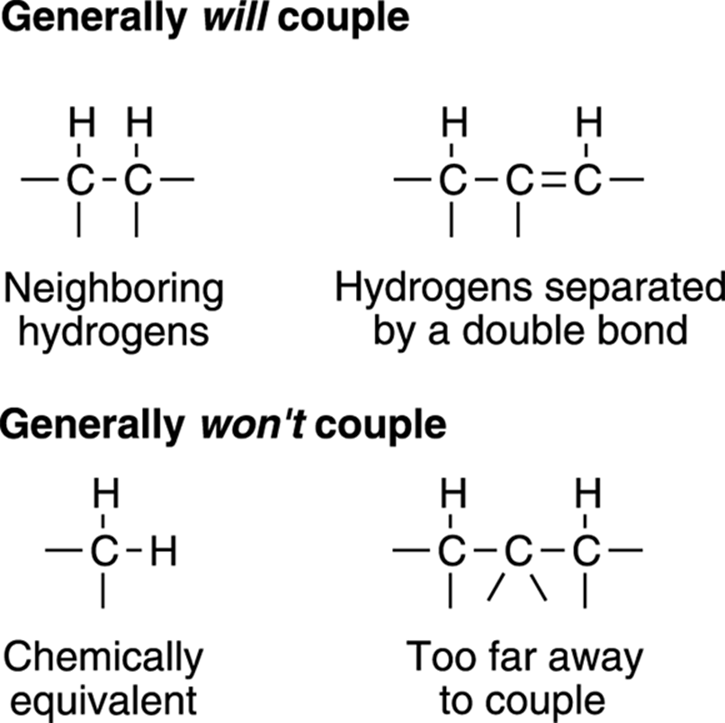
FIGURE 19-16: The types of hydrogens that will and won’t couple.
A peak that does not couple and just shows a single line is called a singlet. The alcohol hydrogen in ethanol does not couple so it gives a singlet. A peak that’s split into two is called a doublet, three a triplet, four a quartet, and so on. You can see the general picture for these kinds of peak splittings in Figure 19-17. The coupling constant, or J value, is proportional to the distance between the lines (or the tops of the peaks) in a signal. This value is given in frequency units (hertz, or Hz), rather than in ppm, to make the coupling constant independent of the size of the external magnetic field. The main point to remember about coupling constants is that hydrogens that couple each other have peaks that are separated by the same coupling constant. This can be a useful piece of information in determining which hydrogens are next to one another, especially when the number of peaks alone is insufficient. Returning to the ethanol example (refer to Figure 19-15), because the CH3 and the CH2 units couple one another, the three peaks around 1.2 ppm are the same distance apart as are the four peaks around 3.7 ppm, and both sets of peaks have the same coupling constant.
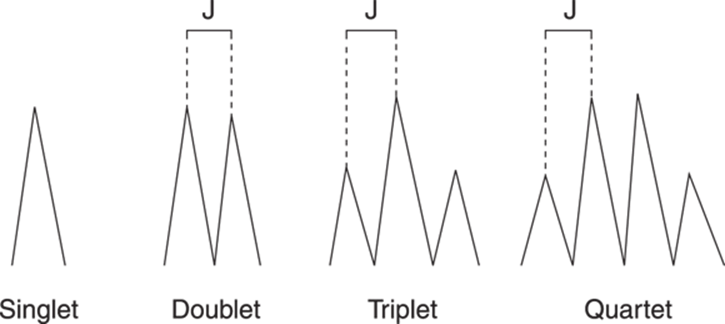
FIGURE 19-17: The coupling constant, or J value for various peaks.
Determining coupling between nonequivalent hydrogens
Many organic molecules — particularly larger molecules — contain hydrogens that are adjacent to two or more nonequivalent hydrogens. In this scenario, adding up all the hydrogen neighbors and applying the n + 1 rule won’t work. Instead, you need to apply the n + 1 rule to each nonequivalent set of hydrogens separately.
Take the case shown in Figure 19-18. To determine the number of peaks that you’ll see for the boxed-in hydrogen — which is surrounded by two nonequivalent sets of hydrogens — you must apply the n + 1 rule to each of the nonequivalent hydrogens separately. For the CH2 unit on the right, the n + 1 rule tells you that this will split the signal into three peaks; for the lone hydrogen on the left, the n + 1 rule tells you that this hydrogen will split the signal into two peaks. To get the total number of peaks you could see, you multiply the two results together. Multiplying three by two gives a total of six peaks for the boxed-in hydrogen signal.
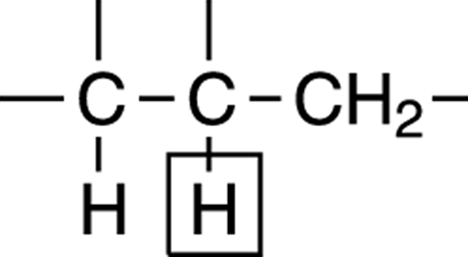
FIGURE 19-18: The hydrogen (proton) surrounded by non-equivalent hydrogens (protons).
In practice, though, you often don’t see all the possible peaks on a spectrum for a hydrogen that’s surrounded by nonequivalent hydrogens, because the coupling constants for the nonequivalent hydrogens often have nearly the same value. When the coupling constants have nearly the same value, the signals overlap, and you observe fewer peaks than the maximum number possible.
 In practice, you can often approximate the number of expected signals for a hydrogen (proton) surrounded by nonequivalent hydrogens. To do this, pretend that the nonequivalent hydrogens are chemically equivalent. Pretend that the CH2 and the lone hydrogen are chemically equivalent. This gives a grand total of three hydrogens, so the n + 1 rule would suggest that if the coupling constant were the same (or nearly the same) the signal would be split into approximately four peaks. Although in theory you could observe up to six peaks for this hydrogen, there’s a fair chance you’ll observe only four.
In practice, you can often approximate the number of expected signals for a hydrogen (proton) surrounded by nonequivalent hydrogens. To do this, pretend that the nonequivalent hydrogens are chemically equivalent. Pretend that the CH2 and the lone hydrogen are chemically equivalent. This gives a grand total of three hydrogens, so the n + 1 rule would suggest that if the coupling constant were the same (or nearly the same) the signal would be split into approximately four peaks. Although in theory you could observe up to six peaks for this hydrogen, there’s a fair chance you’ll observe only four.
Timber! Drawing tree-splitting diagrams
Given the coupling constants of neighboring hydrogens, you can predict the splitting pattern of a hydrogen using what is referred to as a tree diagram. Suppose, for example, you were asked to predict the splitting pattern for the hydrogen Ha in Figure 19-19, and you were given the coupling constant between Ha and Hb (Jab) and the coupling constant between Ha and Hc (Jac).
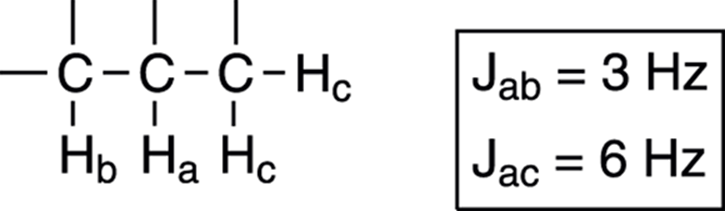
FIGURE 19-19: Predicting coupling patterns.
To draw the tree diagram, start with one of the neighboring hydrogens and determine how many times that hydrogen will split the signal. You’ll get the same result no matter which neighboring hydrogen you start with (in this case, whether you start with Hb or Hc), but it’s often easier to start with the hydrogen that gives the larger J value. So, in this case, start with the Hc protons, because the coupling constant between Ha and Hc is larger than the coupling constant between Ha and Hb. Because there are two Hc hydrogens, these hydrogens split the Ha signal into three peaks following the n + 1 rule.
After you determine that the Hc hydrogens will split the signal into three peaks, begin the tree diagram by making three lines — one that goes straight down, one that goes to the right, and one that goes to the left. Take a look at Figure 19-20 to see how this works. The distance between the peaks is 6 Hz, so in making your tree diagram you may want to use a ruler to measure 6 cm, 6 mm, or 6 pinky-tip lengths to represent the separation between the lines to a proportionally correct distance.
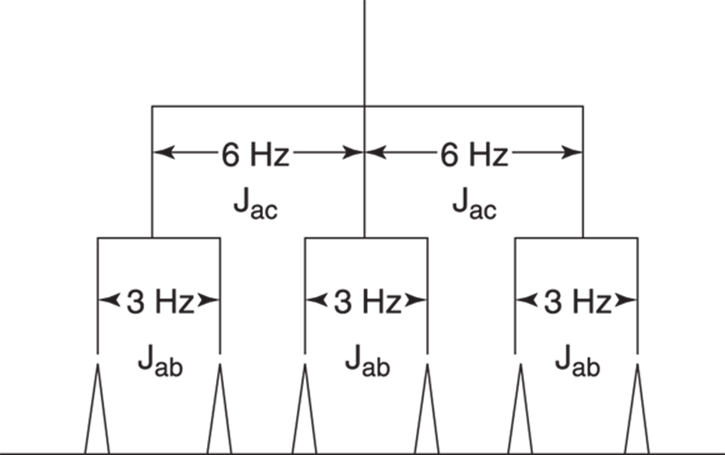
FIGURE 19-20: The tree diagram for the molecule in Figure 19-19, showing the origin of the six peaks for Ha.
 Instead of measuring the distance on your tree diagram, you could draw your tree on graph paper, using one or more squares of the graph paper to represent 1 Hz.
Instead of measuring the distance on your tree diagram, you could draw your tree on graph paper, using one or more squares of the graph paper to represent 1 Hz.
After diagramming the J value for Ha and Hc, do the same for Ha and Hb. Because there is only one Hb hydrogen, the signal will be split further into two, following the n + 1 rule. So, in your drawing, split each of the three lines into two additional lines, keeping a separation of 3 Hz (which would be 3 cm, 3 mm, or 3 pinky-tip lengths across) between the lines. Where each line ends, a peak would be found on the spectrum. In this case, you would expect the signal for that hydrogen to be split into six peaks in the 1H NMR spectrum.
Swapping protons: Exchange
Hydrogens attached to either oxygen or nitrogen generally don’t show any kind of coupling. These peaks are found in 1H NMR spectra as fat singlets. This lack of coupling is caused by chemical exchange.
Small impurities of base or acid in a sample (which are often very difficult to remove) can catalyze the exchange of the hydrogens attached to either nitrogens or oxygens — in other words, the hydrogens of alcohols or amines (see Chapter 5 for more about these functional groups). In solution containing a trace of base, for example, the hydrogens attached to nitrogens and oxygens are deprotonated by the base and then reprotonated very rapidly. Because the NMR experiment takes a long time compared to the quickness of the proton exchange, coupling is not observed for these protons except in meticulously purified samples, or at very low temperatures where this chemical exchange is slower.
 Because this exchange is so quick, to determine whether a peak is an alcohol or an amine, chemists often add a drop of D2O (or heavy water) to the sample. Because deuterons (deuterium nuclei) are not observed in a proton NMR, when the deuterium (hydrogen atom with an additional neutron) replaces a hydrogen through this process of exchange, the peak disappears. This confirms that the peak was either an alcohol or an amine.
Because this exchange is so quick, to determine whether a peak is an alcohol or an amine, chemists often add a drop of D2O (or heavy water) to the sample. Because deuterons (deuterium nuclei) are not observed in a proton NMR, when the deuterium (hydrogen atom with an additional neutron) replaces a hydrogen through this process of exchange, the peak disappears. This confirms that the peak was either an alcohol or an amine.
Considering Carbon NMR
13C NMR is in many ways similar to 1H NMR, only simpler (yay!). Carbon NMR, though, is less sensitive than proton NMR, because only 13C nuclei are NMR active; 12C nuclei are inactive. Because the 13C isotope only has a natural abundance of 1.1 percent (12C makes up most of the rest of the natural abundance), and because the carbon nucleus is less sensitive than a hydrogen nucleus, you generally need more samples for 13C NMR than you do for 1H NMR. For these two reasons, carbon NMR experiments can also take quite a bit longer (many minutes to hours rather than minutes).
Generally, you won’t see either integration or coupling on a 13C spectrum (although occasionally they do pop up). You don’t see carbon-carbon coupling because the natural abundance of 13C is so low — the chance that two 13C nuclei will neighbor each other is so small as to be insignificant. You could see 13C-1H coupling, but most NMR experiments decouple these interactions (doing this increases the intensity of 13C signals, for somewhat complicated reasons). Because of this decoupling, 13C NMR peaks are often just singlets, as can be seen in the 13C spectrum for butyric acid (see Figure 19-21).
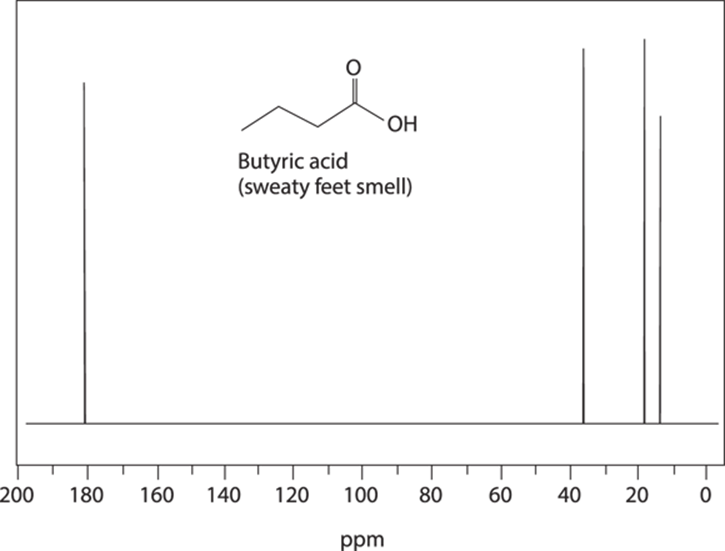
FIGURE 19-21: The 13C spectrum of butyric acid.
Therefore, 13C NMR is mostly useful for telling you the number of different kinds of carbons in a molecule from the number of peaks in the spectrum, while the chemical shift gives you an idea of the chemical environment of those carbons. The range of chemical shift values in a carbon spectrum is quite a bit broader than the shift in a proton NMR — the range is from 0 to 200 ppm, with a 200 ppm peak representing a highly deshielded nucleus. Keep in mind that hydrogen peaks don’t show up on a 13C NMR, just as 13C peaks don’t show up on a 1H NMR spectrum; the13C NMR and 1H NMR spectra must be taken separately (although you can typically use the same NMR spectrometer to take both spectra). Figure 19-22 gives some of the ranges of chemical shift values for particular carbon types.
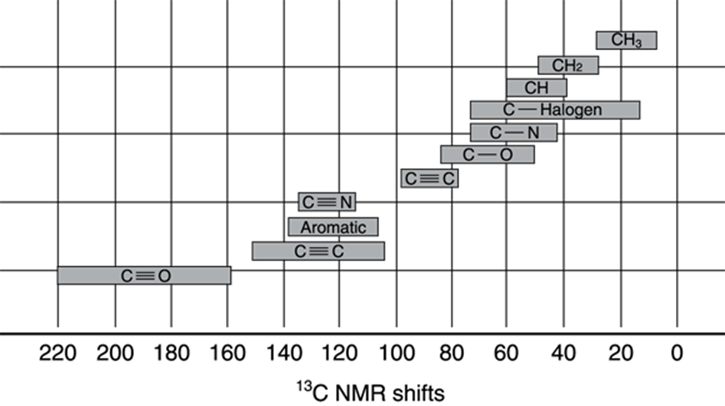
FIGURE 19-22: The range of values for 13C NMR spectra.
Checklist: Putting the Pieces Together
Use the following definitions to help you put everything in this chapter together.
· Chemical shift: Refers to where a peak appears on a spectrum, relative to the reference molecule TMS (also called the δ value). The chemical shift is given in units of parts per million (ppm). It gives you an idea of what kinds of functional groups a hydrogen or carbon is surrounded by.
· Integration: Tells you the area underneath a peak, which in turn gives you information about how many hydrogens a peak represents, relative to the other peaks in the spectrum. Carbon NMR usually does not have integration on the peaks.
· Coupling: Tells you how many hydrogen neighbors a hydrogen sees, following the n + 1 rule. The n + 1 rule can be applied all at once if a hydrogen is surrounded only by chemically equivalent hydrogens. It must be done individually when it’s surrounded by two or more chemically nonequivalent hydrogens. NMR tree-splitting diagrams are used to predict how many peaks will be found in the spectrum of a given hydrogen that’s surrounded by two or more nonequivalent hydrogens. Hydrogens on either nitrogen or oxygen generally don’t couple because of fast exchange processes — these hydrogens generally show up as fat singlets (which go away when the sample is shaken with D2O).
· Coupling constant: Is proportional to the distance between the tops of the peaks in a multiplet. The coupling constant is referred to as the J value (given in units of Hz). This value can tell you which hydrogens are coupled to each other because coupled hydrogens have the same coupling constant.
TURNING NMR TO MRI
NMR has been widely used not only in chemistry, but also in medicine. To take a snapshot of your insides, doctors often perform X-rays. But X-rays have their limitations, particularly in looking at soft tissue. A more powerful technique is magnetic resonance imaging (MRI). MRI machines are huge, specially designed NMR spectrometers that can map what your insides look like in three dimensions and can detect any abnormalities such as tumor growth or bone injury. Instead of sticking a small tube into the spectrometer as you would in a typical NMR spectrometer, in an MRI machine you are the sample, and you’re placed into a very large donut-shaped magnet where a reading can be taken.
The name was changed from NMR to MRI because patients balked when they heard the name nuclear magnetic resonance — nobody wanted to get in a machine that was nuclear! Of course, they didn’t know that nuclear referred to the nucleus of the atom, not to a nuclear reaction. Still, the name was changed to magnetic resonance imaging to make people feel more comfortable about the procedure.
MRI machines are designed to look for the quantity of hydrogen atoms in a given section of the body. Because different kinds of tissue have different numbers of hydrogen atoms than other kinds of tissue (normal brain tissue will have a different quantity of hydrogen than tumor tissue, for example), doctors can map out the densities using a computer and then try to detect any abnormalities. MRI is so valued in modern medicine that in 2003 the Nobel Prize in medicine went to Paul Lauterbur and Peter Mansfield for the development of this technique.