Physical Chemistry Essentials - Hofmann A. 2018
Interactions of Matter with Radiation
13.4 Electron Transition Spectroscopy
Electromagnetic radiation of sufficient energy may not only trigger excitation of rotational or vibrational modes of molecules but also cause transition of electrons into energetically higher orbitals. From the discussion of the hydrogen atom in Sect. 10.1, we know that the allowed electronic energy states vary with the principal quantum number n as per:
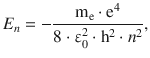
(10.9)
which yields for n = 2 and n = 4:
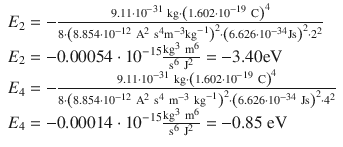
and thus for the difference between both electronic states:
![]()
According to the resonance phenomenon, electromagnetic radiation of the same energy is required to enable a transition between both states. The wavelength of such radiation thus needs to be:
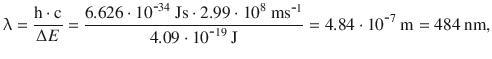
which maps to the visual region of the electromagnetic spectrum. This estimation used the electronic orbitals of the hydrogen atom. In molecules, the energy difference between orbitals is typically found in the region of 1—10 eV. The light required to meet the resonance condition is this in the range of the visual and ultraviolet region of the spectrum.
From the discussion of rota-vibrational spectra in the previous sections, we recall that the vibrational excitation of a molecule causes a simultaneous excitation of rotational modes, i.e. the rotational spectrum is superimposed on any vibrational spectrum. Since the energy quanta meeting the resonance condition for electronic transitions (1—10 eV ≈ 10−19—10−18 J) are one to two orders of magnitude larger than those for vibrational transitions (10−20 J), rota-vibrational transitions will simultaneously occur with electronic transitions. Therefore, rota-vibrational spectra are superimposed on the electronic spectra. The fact that multi-nuclear molecules possess fairly large moments of inertia, the observation of rotational fine structure and vibrational transitions typically occurs as broad bands in the electronic spectra.
In the introduction to this chapter we considered the overall selection rules for transitions between different energy states: one was concerned with the overall electronic spin state and the other with the symmetry of wave functions.
✵ For the electronic spin states, it was stated that the multiplicity M has to remain constant, and therefore the total spin S of the molecule does not change during the transition:
![]()
(13.9)
✵ For the symmetry rules, one needs to consider the symmetry of the wavefunctions (also called parity) as well as the spatial properties of orbitals. If two orbitals involved in a transition do not possess large amplitudes in the same region of space, a transition will not be possible (see also Eq. 13.10).
These selection rules certainly need to be considered for electronic transitions, just as for the rota-vibrational transitions discussed in previous sections. However, further effects will need to be taken into account (see below).
13.4.1 UV/Vis Absorption Spectroscopy
If we consider a diatomic molecule, we can represent the individual electronic states (S 0, S 1, T 1, etc) by their potential energy curves, each of which features the set of vibrational and rotational energy levels. In general, the electronic excited states (S 1, T 1) possess a larger bond distance than the molecule in its ground state. The three potential curves are therefore not only positioned at different levels on the energy scale, but also at different positions with respect to the nuclear displacement scale (Fig. 13.19).
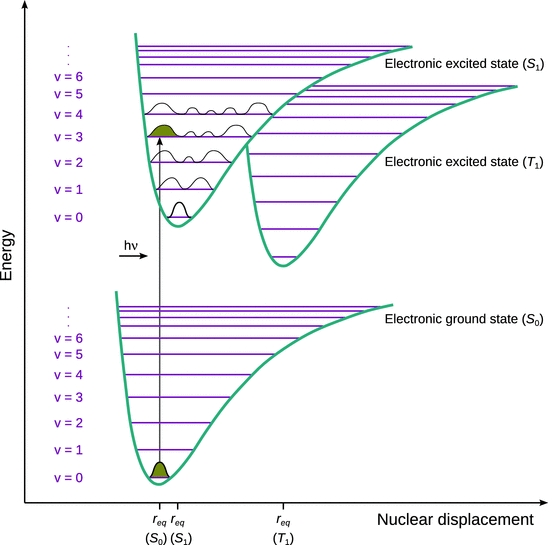
Fig. 13.19
Potential energy diagram sowing different electronic states of a di-atomic molecule and the process of absorption of a photon with energy h·ν
Since the time required for an electronic absorption (10−15 s) is much shorter than the time required to complete a vibration (10−14—10−13 s), one assumes that the atoms remain at their current position while the electronic transition happens. This is the so-called Franck-Condon principle and requires that we draw an electronic transition as a strictly vertical arrow in the potential energy plot in Fig. 13.19. Conceptually, it is based on the Born-Oppenheimer approximation that assumes that the motion of atomic nuclei and electrons in a molecule can be separated.
From previous discussions, we know that the vibrational excited states are essentially not populated when the molecule is in its ground state. When absorbing UV/Vis light (which causes an electronic transition), one thus needs to start in the vibrational ground state of the electronic ground state (S 0v0). As per the resonance condition, an energy quantum will be absorbed only if it exactly matches the energy difference between S 0v0 and a vibrational excited state in the electronic excited state (S 1v i ). Different vibrational levels will be populated to different extents, therefore producing a larger or smaller amplitude in the acquired spectrum. The extent to which a particular vibrational state in the electronic excited state is populated depends on the overlap integral between the probability density Ψ2 (see Sect. 8.3.2) of the starting state (S 0v0) and that of the end state (S 1v i ). The vibrational overlap integral is also known as the Franck-Condon factor. Graphically, this means that the most likely transition is the one where the probability densities of starting and end state share the largest area under their graphs when transitioning strictly vertically. In Fig. 13.19, the largest overlap is between the probability densities of S 0v0 and S 1v3.
We also note that because the start and end vibrational levels of an electronic transition belong to two different potential curves, the vibrational selection rule of Δv = ±1 is no longer valid. The Franck-Condon principle applies to electronic transitions (as opposed to pure rota-vibrational transitions) and thus requires a more complex mathematical treatment than the introductory discussion of the transition dipole momentum (Eq. 13.10), at the centre of which are the overall wavefunctions that are obtained as the product of the individual vibrational, electronic and spin wavefunctions.
13.4.2 Spontaneous Emission from Electronically Excited States
While the elevation of an electron from the ground into an excited state requires the absorption of UV/Vis light, systems may return from the electronic excited to the ground state, in which case there is a possibility that the energy difference is released as a photon. This is the process of emission. When investigating the fabric of atoms, we have seen that atomic absorption and emission spectra produced identical line spectra. In contrast to molecules, however, we did not need to consider rotational or vibrational quantum states. In the following, we will discuss the situation in molecules where the rota-vibrational quantum levels need to be considered.
As discussed in the previous section, upon absorption, electrons typically transition into the first excited singlet state S 1 and the molecule assumes an excited vibrational state (S 1v i ). The life time of such excited states is generally around 10−9—10−5 s and therefore much longer than the time required to complete a vibration (10−14—10−13 s). Most of the vibration al energy in the excited electronic state is thus dissipated as heat into the environment and the molecule subsequently relaxes into the vibrational ground state S 1v0. This process is called internal conversion and is not accompanied by emission of radiation.
Whereas some molecules return to the electronic ground state S 0 by further non-radiative relaxation (internal conversion), others emit a photon in this process and transition into a vibrational excited state of the electronic ground state (S 0v i ). This spontaneous emission of light is called fluorescence. Note that the starting state for the fluorescence emission is always the vibrational ground state of the electronic excited state (here: S 1v0). For this electronic transition, the Franck-Condon principle needs to be applied as introduced in the previous section, since the inter-atomic distances in the molecule remain constant during the electronic transition. The same considerations as for absorption apply, and it turns out that the population of the vibrational end states during the transition are mirrored to to those in the absorption process (see Fig. 13.20). In other words, if the state S 1v3 was the preferred end state during absorption (Fig. 13.19), the most populated end state in the fluorescence emission process will be S 0v3.
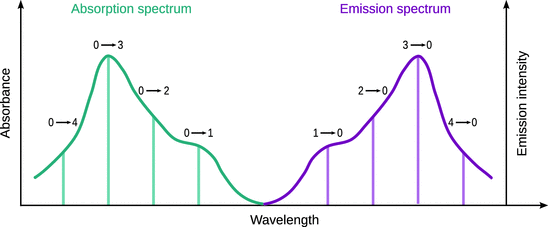
Fig. 13.20
Absorption and fluorescence emission spectra typically are mirror images of each other. The fluorescence spectrum always appears at longer wavelengths than the absorption spectrum ( Stokes shift). The band structure of the absorption spectrum shows the vibrational structure of the excited state. In contrast, the fluorescence spectrum shows the vibrational structure of the ground state
When illustrating electronic transitions in molecules, the scheme showing potential energy curves (Fig. 13.19) are often replaced by so-called Jablonski diagrams (Fig. 13.21). Here, the individual states are depicted by horizontal lines that are grouped together based electronic states; along the y-axis, the states are arranged according to increasing energy. Non-radiative transitions are indicated by dotted arrows and radiative transitions by straight arrows.
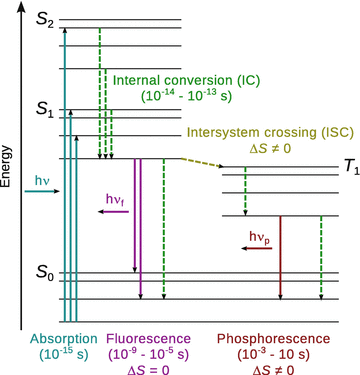
Fig. 13.21
Jablonski diagram explaining transitions in and between electronic ground and excited states
Fluorescence
The spontaneous emission of fluorescence photons following light absorption follows a first-order kinetics and the intensity of light emitted is therefore given by
![]()
(13.35)
where τ is the mean life time of the fluorescent state.
The efficiency of the fluorescence process is expressed by the quantum yield Φ:
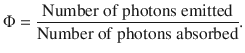
(13.36)
Fluorescent molecules (also called fluorophores) may not operate at 100% efficiency and emit less photons than they absorbed, since the excited state can be deactivated by other processes. These processes include:
✵ internal conversion (here: relaxation from electronic excited to electronic ground state without radiation);
✵ intersystem crossing (change from the singlet to a triplet state of same energy; see below);
✵ quenching (transfer of excess energy to a quenching molecule);
✵ fluorescence resonance energy transfer (transfer of excess energy to an acceptor molecule that subsequently emits a fluorescence photon);
✵ photoreaction.
The rate constant for all deactivation processes is then the sum of the radiative (fluorescence) and all non-radiative processes:
![]()
The reciprocal of this overall rate constant k is the mean life time τ of the fluorophore. The ratio of the rate constant describing the radiative process and the overall rate constant therefore equals the quantum yield:
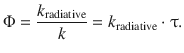
(13.37)
Phosphorescence
In some cases, the triplet state of molecules may possess an intersecting potential curve of lower energy than the excited singlet state (Fig. 13.19). In such cases, it is possible that molecule populates the triplet state after having reached the excited singlet state. This conversion is called intersystem crossing (Fig. 13.21) and, despite being a forbidden process since it involves inversion of the spin of an electron (i.e. ΔS ≠ 0), this selection rule may be weakened if there is a strong spin-orbit interaction such as e.g. in the presence of a heavy atom. Once in the triplet state, the molecule relaxes to the vibrational ground state of the triplet state (T 1v0) from where it can return to the electronic ground state by emission of a photon. This process is known as phosphorescence and also requires a spin inversion, possible only because of the weakening of the spin selection rule. The occurrence of two ’forbidden’ processes leads to a substantial time delay, therefore the photon is emitted at a much later time than the initial absorption.
13.4.3 Stimulated Emission from Electronically Excited States
In addition to the spontaneous emission of light by fluorescence and phosphorescence, molecules can also emit light in a non-spontaneous fashion when returning from an electronic excited to the ground state. Since this process requires stimulation as well as amplification in order to operate, the process is called light amplification by stimulated emission of radiation (laser).
In contrast to the spontaneous emission of light such as in fluorescence and phosphorescence which happens in a statistical fashion, stimulated emission requires the presence of non-participating but stimulating photon of the same energy. Photons resulting from spontaneous emission have a defined energy equal to the difference between the two energy levels between which the transition occurs. The polarisation and direction of travel, however, are random. In the case of stimulated emission, the energy, as well as other properties of the stimulating and emitted photons are the same.
In the cases of spontaneous emission of light, an intrinsic characteristic is that the electronic transitions take place between two different levels, and excited and a ground state. Light amplification in such systems would only be possible if the population of the excited state was larger than that of the ground state. Such a population ratio is called inversion. Even with sustained excitation, the population of the two states in a two-level system can only achieve a balanced distribution; it is not possible to achieve inversion.
However, in three- or four-level systems, inversion may be possible by a process called optical pumping (Fig. 13.22). Absorption of light with appropriate energy can excite molecules from the ground state to level 1, from which they transit into level 2. If the life time of level 2 is much larger than that of level 1, it is possible to build up a large population of level 2. From this state, the molecule can transition to level 3 by stimulated emission and thus release a photon. If the life time of level 3 is much shorter than that of level 2, the molecule quickly relaxes into the ground state from which it can be excited again into level 1. Importantly, the population of level 3 needs to be fairly small compared to level 2. If this process is repeated many times by means of a constant feedback, an oscillating system is generated that can produce an enormous amplification. This is technically achieved in an optical resonator that sends the photons multiple times through a tube; oscillating properties are possible if the resonator length is an integer multiple of half of the wavelength of the emitted light.
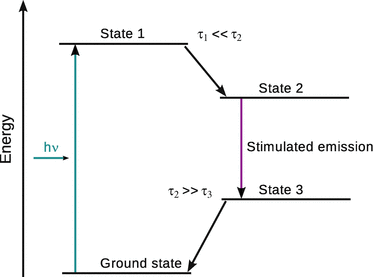
Fig. 13.22
Schematics of optical pumping in a four-level system
The laser medium can be a gas, liquid, or solid semi-conducting material. The excitation of the laser medium may be achieved electrically, with light flashes or even the reaction enthalpy of an exothermic chemical reaction. After excitation, a photon may be emitted spontaneously in the long direction of the resonator. This photon can serve as the stimulating photon that elicits release of another photon by a neighbouring molecule. As this process continues, more and more photons are emitted which then reach a mirror at one end of the resonator. The light is reflected back into the laser medium and leads to further amplification as it travels into the opposite direction. At the other end of the resonator is a partially transparent mirror that reflects most of the light back into the medium. Owing to the relationship between the resonator length and the wavelength of the emitted light, an oscillation results since forth- and back-running light waves are always in phase. Some of the light can leave the resonator through the partially transparent mirror (output coupler) such as to be used for particular purposes.