A Book of Abstract Algebra, Second Edition (1982)

Chapter 9. ISOMORPHISM

Human perception, as well as the “perception” of so-called intelligent machines, is based on the ability to recognize the same structure in different guises. It is the faculty for discerning, in different objects, the same relationships between their parts.

The dictionary tells us that two things are “isomorphic” if they have the same structure. The notion of isomorphism—of having the same structure—is central to every branch of mathematics and permeates all of abstract reasoning. It is an expression of the simple fact that objects may be different in substance but identical in form.

In geometry there are several kinds of isomorphism, the simplest being congruence and similarity. Two geometric figures are congruent if there exists a plane motion which makes one figure coincide with the other; they are similar if there exists a transformation of the plane, magnifying or shrinking lengths in a fixed ratio, which (again) makes one figure coincide with the other.

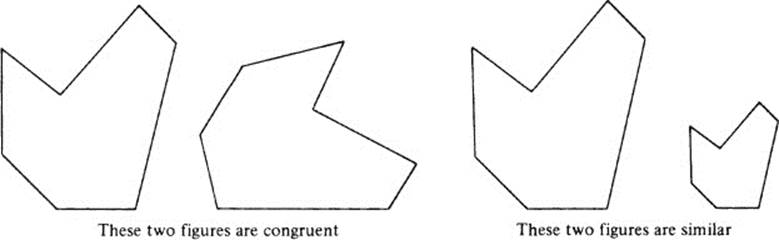
We do not even need to venture into mathematics to meet some simple examples of isomorphism. For instance, the two palindromes

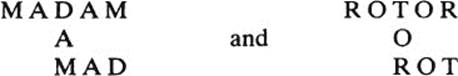
are different, but obviously isomorphic; indeed, the first one coincides with the second if we replace M by R, A by O, and D by T.

Here is an example from applied mathematics: A flow network is a set of points, with arrows joining some of the points. Such networks are used to represent flows of cash or goods, channels of communication, electric circuits, and so on. The flow networks (A) and (B), below, are different, but can be shown to be isomorphic. Indeed, (A) can be made to coincide with (B) if we superimpose point 1 on point 6, point 2 on point 5, point 3 on point 8, and point 4 on point 7. (A) and (B) then coincide in the sense of having the same points joined by arrows in the same direction. Thus, network (A) is transformed into network (B) if we replace points 1 by 6, 2 by 5, 3 by 8, and 4 by 7. The one-to-one correspondence which carries out this transformation, namely,

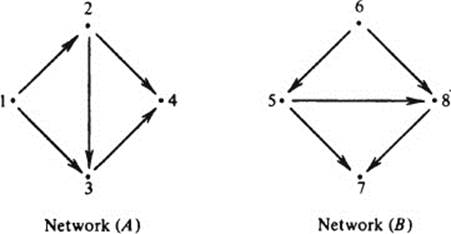
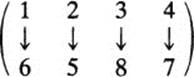
is called an isomorphism from network (A) to network (B), for it transforms (A) into (B).

Incidentally, the one-to-one correspondence

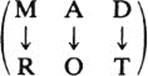
is an isomorphism between the two palindromes of the preceding example, for it transforms the first palindrome into the second.

Our next and final example is from algebra. Consider the two groups G₁ and G₂ described below:

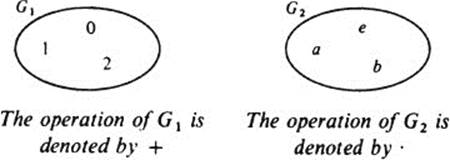
Table of G₁

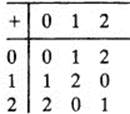
Table of G₂

G₁ and G₂ are different, but isomorphic. Indeed, if in G₁ we replace 0 by e, 1 by a, and 2 by b, then G₁ coincides with G₂, the table of G₁ being transformed into the table of G₂. In other words, the one-to-one correspondence

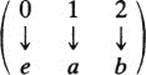
transforms G₁ to G₂. It is called an isomorphism from G₁ to G₂. Finally, because there exists an isomorphism from G₁ to G₂, G₁ and G₂ are isomorphic to each other.

In general, by an isomorphism between two groups we mean a one-to-one correspondence between them which transforms one of the groups into the other. If there exists an isomorphism from one of the groups to the other, we say they are isomorphic. Let us be more specific:

If G₁ and G₂ are any groups, an isomorphism from G₁ to G₂ is a one-to-one correspondence f from G₁ to G₂ with the following property: For every pair of elements a and b in G₁,

If f(a) = a′ and f(b) = b′ then f(ab) = a′b′ (1)

In other words, if/matches a with a′ and b with b′ it must match ab with a′b′.

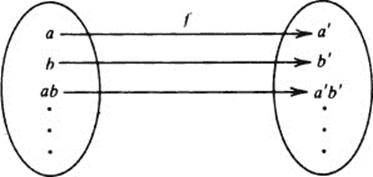
It is easy to see that if /has this property it transforms the table of G₁ into the table of G₂:

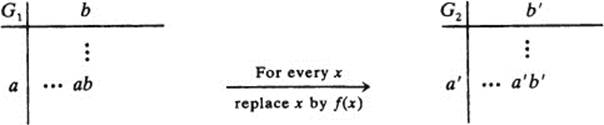
There is another, equivalent way of looking at this situation: If two groups G₁ and G₂ are isomorphic, we can say the two groups are actually the same, except that the elements of G₁ have different names from the elements of G₂. G₁ becomes exactly G₂ if we rename its elements. The function which does the renaming is an isomorphism from G₁ to G₂. Thus, in our last example, if 0 is renamed e, 1 is renamed a, and 2 is renamed 6, G₁ becomes exactly G₂, with the same table. (Note that we have also renamed the operation: it was called + in G₁ and · in G₂.)

By the way, property (1) may be written more concisely as follows:

f(ab) = f(a)f(b) (2)

So we may sum up our definition of isomorphism in the following way:

Definition Let G₁ and G₂ be groups. A bijective function f : G₁ → G₂ with the property that for any two elements a and b in G₁,

f(ab) = f(a)f(b) (2)

is called an isomorphism from G₁ to G₂.

If there exists an isomorphism from G₁ to G₂, we say that G₁ is isomorphic to G₂.

If there exists an isomorphism f from G₁ to G₂, in other words, if G₁ is isomorphic to G₂, we symbolize this fact by writing

G₁ ≅ G₂

to be read, “G₁ is isomorphic to G₂.”

How does one recognize if two groups are isomorphic? This is an important question, and not quite so easy to answer as it may appear. There is no way of spontaneously recognizing whether two groups G₁ and G₂ are isomorphic. Rather, the groups must be carefully tested according to the above definition.

G₁ and G₂ are isomorphic if there exists an isomorphism from G₁ to G₂. Therefore, the burden of proof is upon us to find an isomorphism from G₁ to G₂, and show that it is an isomorphism. In other words, we must go through the following steps:

1.Make an educated guess, and come up with a function f : G₁ G₂ which looks as though it might be an isomorphism.

2.Check that f is injective and surjective (hence bijective).

3.Check that f satisfies the identity

f(ab) = f(a)f(b)

Here’s an example: is the group of the real numbers with the operation of addition. ^pos is the group of the positive real numbers with the operation of multiplication. It is an interesting fact that and ^pos are isomorphic. To see this, let us go through the steps outlined above:

1.The educated guess: The exponential function f(x) = e^x is a function from to ^pos which, if we recall its properties, might do the trick.

2.f is injective: Indeed, if f(a) = f(b), that is, e^a = e^b, then, taking the natural log on both sides, we get a = b.

f is surjective: Indeed, if y ∈ ^pos, that is, if y is any positive real number, then y = e^{ln y} = f(ln y); thus, y = f(x) for x = ln y.

3.It is well known that e^a+b = e^a · e^b, that is,

f(a + b) = f(a) · f(b)

Incidentally, note carefully that the operation of is +, whereas the operation of ^pos is ·. That is the reason we have to use + on the left side of the preceding equation, and · on the right side of the equation.

How does one recognize when two groups are not isomorphic? In practice it is usually easier to show that two groups are not isomorphic than to show they are. Remember that if two groups are isomorphic they are replicas of each other; their elements (and their operation) may be named differently, but in all other respects they are the same and share the same properties. Thus, if a group G₁ has a property which group G₂ does not have (or vice versa), they are not isomorphic! Here are some examples of properties to look out for:

1.Perhaps G₁ is commutative, and G₂ is not.

2.Perhaps G₁ has an element which is its own inverse, and G₂ does not.

3.Perhaps G₁ is generated by two elements, whereas G₂ is not generated by any choice of two of its elements.

4.Perhaps every element of G₁ is the square of an element of G₁, whereas G₂ does not have this property.

This list is by no means exhaustive; it merely illustrates the kind of things to be on the lookout for. Incidentally, the kind of properties to watch for are properties which do not depend merely on the names assigned to individual elements; for instance, in our last example, 0 ∈ G₁ and 0 ∉ G₂, but nevertheless G₁ and G₂ are isomorphic.

Finally, let us state the obvious: if G₁ and G₂ cannot be put in one-to-one correspondence (say, G₁ has more elements that G₂), clearly they cannot be isomorphic.

In the early days of modern algebra the word “group” had a different meaning from the meaning it has today. In those days a group always meant a group of permutations. The only groups mathematicians used were groups whose elements were permutations of some fixed set and whose operation was composition.

There is something comforting about working with tangible, concrete things, such as groups of permutations of a set. At all times we have a clear picture of what it is we are working with. Later, as the axiomatic method reshaped algebra, a group came to mean any set with any associative operation having a neutral element and allowing each element an inverse. The new notion of group pleases mathematicans because it is simpler and more lean and sparing than the old notion of groups of permutations; it is also more general because it allows many new things to be groups which are not groups of permutations. However, it is harder to visualize, precisely because so many different things can be groups.

It was therefore a great revelation when, about 100 years ago, Arthur Cayley discovered that every group is isomorphic to a group of permutations. Roughly, this means that the groups of permutations are actually all the groups there are! Every group is (or is a carbon copy of) a group of permutations. This great result is a classic theorem of modern algebra. As a bonanza, its proof is not very difficult.

Cayley’s Theorem Every group is isomorphic to a group of permutations.

PROOF: Let G be a group; we wish to show that G is isomorphic to a group of permutations. The first question to ask is, “What group of permutations? Permutations of what set?” (After all, every permutation must be a permutation of some fixed set.) Well, the one set we have at hand is the set G, so we had better fix our attention on permutations of G. The way we match up elements of G with permutations of G is quite interesting:

With each element a in G we associate a function π_a : G → G defined by

π_a(x) = ax

In other words, π_a is the function whose rule may be described by the words “multiply on the left by a,” We will now show that π_a is a permutation of G:

1.π_a is injective: Indeed, if π_a(x₁) = π_a(x₂), then ax₁ = ax₂, so by the cancellation law, x₁ = x₂.

2.π_a is surjective: For if y ∈ G, then y = a(a⁻¹ y) = π_a(a⁻¹ y). Thus, each y in G is equal to π_a(x) for x = a⁻¹ y.

3.Since π_a is an injective and surjective function from G to G, π_a is a permutation of G.

Let us remember that we have a permutation π_a for each element a in G; for example, if b and c are other elements in G, π_b is the permutation “multiply on the left by b,” π_c is the permutation “multiply on the left by c,” and so on. In general, let G* denote the set of all the permutations π_a as a ranges over all the elements of G:

G* = {π_a : a ∈ G}

Observe now that G* is a set consisting of permutations of G—but not necessarily all the permutations of G. In Chapter 7 we used the symbol S_G to designate the group of all the permutations of G. We must show now that G* is a subgroup of S_G, for that will prove that G* is a group of permutations.

To prove that G* is a subgroup of S_G, we must show that G* is closed with respect to composition, and closed with respect to inverses. That is, we must show that if π_a and π_b are any elements of G*, their composite π_a ∘ π_b is also in G*; and if π_a is any element of G*, its inverse is in G*.

First, we claim that if a and b are any elements of G, then

π_a ∘ π_b = π_ab (3)

To show that π_a ∘ π_b and π_ab are the same, we must show that they have the same effect on every element x: that is, we must prove the identity [π_a ∘ π_b](x) = π_ab(x). Well, [π_a ∘ π_b](x) = π_a(π_b(x)) = π_a(bx) = a(bx) = (ab)x = π_ab(x). Thus, π_a ∘ π_b = π_ab; this proves that the composite of any two members Z_a and π_b of G* is another member π_ab of G*. Thus, G* is closed with respect to composition.

It is each to see that π_e is the identity function: indeed,

π_e(x) = ex = x

In other words, π_e is the identity element of S_G.

Finally, by Equation (3),

π_a ∘ π_a − 1 = π_aa − 1 = π_e

So by Theorem 2 of Chapter 4, the inverse of π_a is π_a⁻¹. This proves that the inverse of any member π_a of G* is another member π_a⁻¹ of G*. Thus, G* is closed with respect to inverses.

Since G* is closed with respect to composition and inverses, G* is a subgroup of S_G.

We are now in the final lap of our proof. We have a group of permutations G*, and it remains only to show that G is isomorphic to G*. To do this, we must find an isomorphism f : G → G*. Let f be the function

f(a) = π_a

In other words, f matches each element a in G with the permutation π_a in G*. We can quickly show that f is an isomorphism:

1.f is injective: Indeed, if f(a) = f(b) then π_a = π_b. Thus, π_a(e) = π_b(e), that is, ae = be, so, finally, a = b.

2.f is surjective: Indeed, every element of G* is some π_a, and π_a = f(a).

3.Lastly, f(ab) = π_ab = π_a ∘ π_b = f(a) ∘ f(b).

Thus, f is an isomorphism, and so G ≅ G*. ■

EXERCISES

A. Isomorphism Is an Equivalence Relation among Groups

The following three facts about isomorphism are true for all groups:

(i) Every group is isomorphic to itself.

(ii) If G₁ ≅ G₂, then G₂ ≅ G₁.

(iii) If G₁ ≅ G₂ and G₂ ≅ G₃, then G₁ ≅ G₃.

Fact (i) asserts that for any group G, there exists an isomorphism from G to G.

Fact (ii) asserts that, if there is an isomorphism f from G₁ to G₂, there must be some isomorphism from G₂ to G₁. Well, the inverse of f is such an isomorphism.

Fact (iii) asserts that, if there are isomorphisms f : G₁ → G₂ and g : G₂ → G₃, there must be an isomorphism from G₁ to G₃. One can easily guess that g ∘ f is such an isomorphism. The details of facts (i), (ii), and (iii) are left as exercises.

1 Let G be any group. If ε : G → G is the identity function, ε(x) = x, show that ε is an isomorphism.

2 Let G₁ and G₂ be groups, and f : G₁ → G₂ an isomorphism. Show that f⁻¹: G₂ → G₁ is an isomorphism. [HINT: Review the discussion of inverse functions at the end of Chapter 6. Then, for arbitrary elements c, d ∈ G₂, there exist a, b ∈ G₁, such that c = f(a) and d = f(b). Note that a = f⁻¹(c) and b = f⁻¹(d). Show that f⁻¹(cd) = f⁻¹(c)f⁻¹(d).]

3 Let G₁, G₂, and G₃ be groups, and let f: G₁ → G₂ and g : G₂ → G₃ be isomorphisms. Prove that g ∘ f : G₁ → G₃ is an isomorphism.

B. Elements Which Correspond under an Isomorphism

Recall that an isomorphism f from G₁ to G₂ is a one-to-one correspondence between G₁ and G₂ satisfying f(ab) = f(a)f(b). f matches every element of G_l with a corresponding element of G₂. It is important to note that:

(i)f matches the neutral element of G₁ with the neutral element of G₂.

(ii)If f matches an element x in G₁ with y in G₂, then, necessarily, f matches x^−l with y⁻¹ That is, if x ↔ y, then x^−l ↔ y⁻¹.

(iii)f matches a generator of G₁ with a generator of G₂.

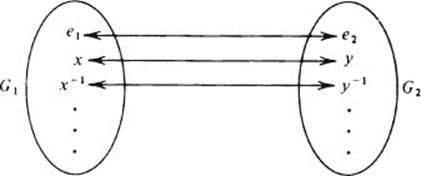
The details of these statements are now left as an exercise. Let G₁ and G₂ be groups, and let f : G₁ → G₂ be an isomorphism.

1 If e₁ denotes the neutral element of G₁ and e₂ denotes the neutral element of G₂, prove that f(e₁) = e₂. [HINT: In any group, there is exactly one neutral element; show that f(e₁) is the neutral element of G₂.]

2 Prove that for each element a in G₁ f(a^−l) = [f(a)]⁻¹. (HINT: You may use Theorem 2 of Chapter 4.)

3 If G₁ is a cyclic group with generator a, prove that G₂ is also a cyclic group, with generator f(a).

C. Isomorphism of Some Finite Groups

In each of the following, G and H are finite groups. Determine whether or not G ≅ H. Prove your answer in either case.

To find an isomorphism from G to H will require a little ingenuity. For example, if G and H are cyclic groups, it is clear that we must match a generator a of G with a generator b of H; that is, f(a) = b. Then f(aa) = bb, f(aaa) = bbb, and so on. If G and H are not cyclic, we have other ways: for example, if G has an element which is its own inverse, it must be matched with an element of H having the same property. Often, the specifics of a problem will suggest an isomorphism, if we keep our eyes open.

To prove that a specific one-to-one correspondence f : G → H is an isomorphism, we may check that it transforms the table of G into the table of H.

# 1 G is the checkerboard game group of Chapter 3, Exercise D. H is the group of the complex numbers {i, −i, 1, −1} under multiplication.

2 G is the same as in part 1. H = ₄.

3 G is the group P₂ of subsets of a two-element set. (See Chapter 3, Exercise C.) H is as in part 1.

# 4 G is S₃, H is the group of matrices described on page 28 of the text.

5 G is the coin game group of Chapter 3, Exercise E. H is D₄, the group of symmetries of the square.

6 G is the group of symmetries of the rectangle. H is as in part 1.

D. Separating Groups into Isomorphism Classes

Each of the following is a set of four groups. In each set, determine which groups are isomorphic to which others. Prove your answers, and use Exercise A3 where convenient.

1 _{4 2} × ₂ P₂ V

[P₂ denotes the group of subsets of a two-element set. (See Chapter 3, Exercise C.) V denotes the group of the four complex numbers {i, −i, 1, −1} with respect to multiplication.]

2 S_{3 6 3} × ₂

( denotes the group {1,2,3,4,5,6} with multiplication modulo 7. The product modulo 7 of a and b is the remainder of ab after division by 7.)

3 ₈ P_{3 2} × ₂ × ₂ D₄

(D₄ is the group of symmetries of the square.)

4 The groups having the following Cayley diagrams:

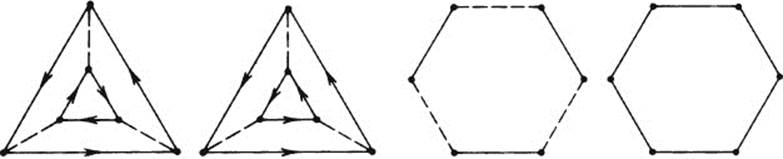
E. Isomorphism of Infinite Groups

# 1 Let E designate the group of all the even integers, with respect to addition. Prove that ≅ E.

2 Let G be the group {10ⁿ : n ∈ } with respect to multiplication. Prove that G ≅ . (Remember that the operation of is addition.)

3 Prove that = × .

4 We have seen in the text that is isomorphic to ^pos. Prove that is not isomorphic to * (the multiplicative group of the nonzero real numbers). (HINT: Consider the properties of the number −1 in *. Does have any element with those properties?)

5 Prove that is not isomorphic to .

6 We have seen that ≅ ^pos. However, prove that is not isomorphic to ^pos. (^pos is the multiplicative group of positive rational numbers.)

F. Isomorphism of Groups Given by Generators and Defining Equations

If a group G is generated, say, by a, b, and c, then a set of equations involving a, b, and c is called a set of defining equations for G if these equations completely determine the table of G. (See end of Chapter 5.) If G′ is another group, generated by elements a′, b′, and c′ satisfying the same defining equations as a, b, and c, then G′ has the same table as G (because the tables of G and G′ are completely determined by the defining equations, which are the same for G as for G′).

Consequently, if we know generators and defining equations for two groups G and G′, and if we are able to match the generators of G with those of G′ so that the defining equations are the same, we may conclude that G ≅ G′.

Prove that the following pairs of groups G, G′ are isomorphic.

# 1 G = the subgroup of S₄ generated by (24) and (1234); G′ = {e, a, b, b², b³, ab, ab², ab³} where a² = e, b⁴ = e, and ba = ab³.

2 G = S₃; G′ = {e, a, b, ab, aba, abab} where a² = e, b² = e, and bab = aba.

3 G = D₄; G′ = {e, a, b, ab, aba, (ab)², ba, bab} where a² = b² = e and (ab)⁴ = e.

4 G = ₂ × ₂ × ₂; G′ = {e, a, b, c, ab, ac, bc, abc} where a² = b² = c² = e and (ab)² = (bc)² = (ac)² = e.

G. Isomorphic Groups on the Set

1 G is the set {x ∈ : x ≠ −1} with the operation x * y = x + y + xy. Show that f(x) = x − 1 is an isomorphism from * to G. Thus, * ≅ G.

2 G is the set of the real numbers with the operation x * y = x + y + l. Find an isomorphism f : → G and show that it is an isomorphism.

3 G is the set of the nonzero real numbers with the operation x * y = xy/2. Find an isomorphism from * to G.

4 Show that f(x, y) = (−1)^y x is an isomorphism from ^pos × ₂ to *. (REMARK: To combine elements of ^pos × ₂, one multiplies first components, adds second components.) Conclude that * ≅ ^pos × ₂.

H. Some General Properties of Isomorphism

1 Let G and H be groups. Prove that G × H ≅ H × G.

# 2 If G₁ ≅ G₂ and H₁ ≅ H₂, then G₁ × H₁ ≅ G₂ × H₂.

3 Let G be any group. Prove that G is abelian iff the function f(x) = x⁻¹ is an isomorphism from G to G.

4 Let G be any group, with its operation denoted multiplicatively. Let H be a group with the same set as G and let its operation be defined by x * y = y · x (where · is the operation of G). Prove that G ≅ H.

5 Let c be a fixed element of G. Let H be a group with the same set as G, and with the operation x * y = xcy. Prove that the function f(x) = c^−lx is an isomorphism from G to H.

I. Group Automorphisms

If G is a group, an automorphism of G is an isomorphism from G to G. We have seen (Exercise A1) that the identity function ε(x) = x is an automorphism of G. However, many groups have other automorphisms besides this obvious one.

1 Verify that

is an automorphism of ₆.

2 Verify that

and

are all automorphisms of ₅.

3 If G is any group, and a is any element of G, prove that f(x) = axa’⁻¹ is an automorphism of G.

4 Since each automorphism of G is a bijective function from G to G, it is a permutation of G. Prove the set

Aut(G)

of all the automorphisms of G is a subgroup of S_G. (Remember that the operation is composition.)

J. Regular Representation of Groups

By Cayley’s theorem, every group G is isomorphic to a group G* of permutations of G. Recall that we match each element a in G with the permutation π_a defined by π_a = ax, that is, the rule “multiply on the left by a.” We let G* = {π_a : a ∈ G}; with the operation ∘ of composition it is a group of permutations, called the left regular representation of G. (It is called a “representation” of G because it is isomorphic to G.)

Instead of using the permutations π_a, we could just as well have used the permutations ρ_a defined by ρ_a(x) = xa, that is, “multiply on the right by a.” The group G^ρ = {ρ_a: a ∈ G} is called the right regular representation of G.

If G is commutative, there is no difference between right and left multiplication, so G* and G^ρ are the same, and are simply called the regular representation of G. Also, if the operation of G is denoted by +, the permutation corresponding to a is “add a” instead of “multiply by a.”

Example The regular representation of ₃ consists of the following permutations:

The regular representation of ₃ has the following table:

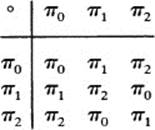
The function

is easily seen to be an isomorphism from ₃ to its regular representation.

Find the right and left regular representation of each of the following groups, and compute their tables. (If the group is abelian, find its regular representation.)

1 P₂, the group of subsets of a two-element set. (See Chapter 3, Exercise C.)

2 ₄.

3 The group G of matrices described on page 28 of the text.