A Book of Abstract Algebra, Second Edition (1982)
Chapter 8. PERMUTATIONS OF A FINITE SET
Permutations of finite sets are used in every branch of mathematics—for example, in geometry, in statistics, in elementary algebra—and they have a myriad of applications in science and technology. Because of their practical importance, this chapter will be devoted to the study of a few special properties of permutations of finite sets.
If n is a positive integer, consider a set of n elements. It makes no difference which specific set we consider, just as long as it has n elements; so let us take the set {1,2,…, n). We have already seen that the group of all the permutations of this set is called the symmetric group on η elements and is denoted by Sn. In the remainder of this chapter, when we say “permutation” we will invariably mean a permutation of the set {1,2,…, n} for an arbitrary positive integer n.
One of the most characteristic activities of science (any kind of science) is to try to separate complex things into their simplest component parts. This intellectual “divide and conquer” helps us to understand complicated processes and solve difficult problems. The savvy mathematician never misses the chance of doing this whenever the opportunity presents itself. We will see now that every permutation can be decomposed into simple parts called “cycles,” and these cycles are, in a sense, the most basic kind of permutations.
We begin with an example: take, for instance, the permutation
![]()
and look at how f moves the elements in its domain:
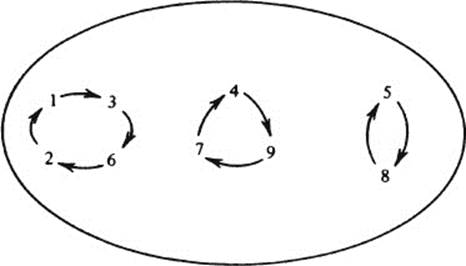
Notice how f decomposes its domain into three separate subsets, so that, in each subset, the elements are permuted cyclically so as to form a closed chain. These closed chains may be considered to be the component parts of the permutation; they are called “cycles.” (This word will be carefully defined in a moment.) Every permutation breaks down, just as this one did, into separate cycles.
Let a1, a2, …, as be distinct elements of the set {1,2,…, n}. By the cycle (a1a2 … as) we mean the permutation
![]()
of {1,2,…, n} which carries a1 to a2, a2 to a3,…, as−1 to as, and as to a1, while leaving all the remaining elements of {1,2,…,n} fixed.
For instance, in s6, the cycle (1426) is the permutation
![]()
In S5,the cycle (254) is the permutation
![]()
Because cycles are permutations, we may form the compositeof two cycles in the usual manner. The composite of cycles is generally called their productand it is customary to omit the symbol °. For example, in S5,
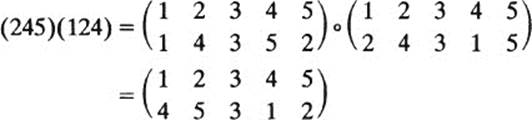
Actually, it is very easy to compute the product of two cycles by reasoning in the following manner: Let us continue with the same example,
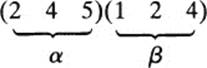
Remember that the permutation on the right is applied first, and the permutation on the left is applied next. Now,
β carries 1 to 2, and α carries 2 to 4; hence αβ carries 1 to 4.
β carries 2 to 4, and α carries 4 to 5; hence αβ carries 2 to 5 .
β leaves 3 fixed and so does α ; hence αβ leaves 3 fixed.
β carries 4 to 1 and α leaves 1 fixed, so αβ carries 4 to 1.
β leaves 5 fixed and α carries 5 to 2; hence αβ carries 5 to 2.
If (a1a2…as) is a cycle, the integer s is called its length; thus, (a1a2…as) is a cycle of length s. For example, (1532) is a cycle of length 4.
If two cycles have no elements in common they are said to be disjoint. For example, (132) and (465) are disjoint cycles, but (132) and (453) are not disjoint. Disjoint cycles commute: that is, if (a1…ar) and (bl…bs) are disjoint, then
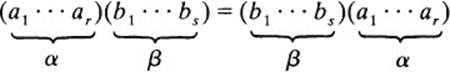
It is easy to see why this is true: α moves the a’s but not the fc’s, while β moves the ft’s but not the a’s. Thus, if β carries bi to bj, then αβ does the same, and so does βα Similarly, if a carries ah to ak then βα does the same, and so does αβ.
We are now ready to prove what was asserted at the beginning of this chapter: Every permutation can be decomposed into cycles—in fact, into disjoint cycles. More precisely, we can state the following:
Theorem 1 Every permutation is either the identity, a single cycle, or a product of disjoint cycles.
We begin with an example, because the proof uses the same technique as the example. Consider the permutation
![]()
and let us write f as a product of disjoint cycles. We begin with 1 and note that
![]()
We have come a complete circle and found our first cycle, which is (135). Next, we take the first number which hasn’t yet been used, namely, 2. We see that
![]()
Again we have come a complete circle and found another cycle, which is (24). The only remaining number is 6, which/leaves fixed. We are done:
f = (135)(24)
The proof for any permutation f follows the same pattern as the example. Let a1 be the first number in {1,…, n) such that f(a1)≠ a1. Let a2 = f(a1), a3 = f(a2), and so on in succession until we come to our first repetition, that is, until f(ak) is equal to one of the numbers a1, a2,…, ak−1. Say f(ak) = ai If ai is not a1,we have
![]()
so ai is the image of two elements, ak and ai−1, which is impossible because f is bijective. Thus, ai = a1, and therefore f(ak) = a1.We have come a complete circle and found our first cycle, namely, (a1a2 ··· ak).
Next, let b1 be the first number which has not yet been examined and such that f(b1) ≠ b1. We let b2 = f(b1), b3 = f(b2), and proceed as before to obtain the next cycle, say (b1 ··· bt). Obviously (b1 ··· bt) is disjoint from (a1 …, ak). We continue this process until all the numbers in {1, …, n) have been exhausted. This concludes the proof.
Incidentally, it is easy to see that this product of cycles is unique, except for the order of the factors.
Now our curiosity may prod us to ask: once a permutation has been written as a product of disjoint cycles, has it been simplified as much as possible? Or is there some way of simplifying it further?
A cycle of length 2 is called a transposition. In other words, a transposition is a cycle (ai, aj) which interchanges the two numbers ai and aj.It is a fact both remarkable and trivial that every cycle can be expressed as a product of one or more transpositions. In fact,
(a1a2 … ar) = (arar−1)(arar−2) … (ara3)(ara2ara1)
which may be verified by direct computation. For example,
(12345) = (54)(53)(52)(51)
However, there is more than one way to write a given permutation as a product of transpositions. For example, (12345) may also be expressed as a product of transpositions in the following ways:
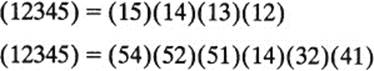
as well as in many other ways.
Thus, every permutation, after it has been decomposed into disjoint cycles, may be broken down further and expressed as a product of transpositions. However, the expression as a product of transpositions is not unique, and even the number of transpositions involved is not unique.
Nevertheless, when a permutation π is written as a product of transpositions, one property of this expression is unique: the number of transpositions involved is either always even or always odd. (This fact will be proved in a moment.) For example, we have just seen that (12345) can be written as a product of four transpositions and also as a product of six transpositions; it can be written in many other ways, but always as a product of an even number of transpositions. Likewise, (1234) can be decomposed in many ways into transpositions, but always an odd number of transpositions.
A permutation is called even if it is a product of an even number of transpositions, and odd if it is a product of an odd number of transpositions. What we are asserting, therefore, is that every permutation is unambiguously either odd or even.
This may seem like a pretty useless fact—but actually the very opposite is true. A number of great theorems of mathematics depend for their proof (at that crucial step when the razor of logic makes its decisive cut) on none other but the distinction between even and odd permutations.
We begin by showing that the identity permutation, ε, is an even permutation.
Theorem 2 No matter how ε is written as a product of transpositions, the number of transpositions is even.
PROOF: Let t1, t2, …, tm be m transpositions, and suppose that
ε = t1t2 … tm (1)
We aim to prove that ε can be rewritten as a product of m − 2 transpositions. We will then be done: for if ε were equal to a product of an odd number of transpositions, and we were able to rewrite this product repeatedly, each time with two fewer transpositions, then eventually we would get ε equal to a single transposition (ab), and this is impossible.
Let x be any numeral appearing in one of the transpositions t2, …, tm. Let tk = (xa), and suppose tk is the last transposition in Equation (1) (reading from left to right) in which x appears:
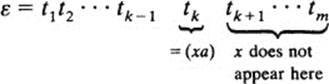
Now, tk−1 is a transposition which is either equal to (xa), or else one or both of its components are different from χ and a. This gives four possibilities, which we now treat as four separate cases.
Case I tk−1 = (xa).
Then tk−1tk = (xa)(xa), which is equal to the identity permutation. Thus, tk−1tk may be removed without changing Equation (1). As a result, ε is a product of m − 2 transpositions, as required.
Case II tk−1 = (xb) where b ≠ x,a.
Then tk−1)tk = (xb)(xa)
But (xb)(xa) = (xa)(ab)
We replace tk−1 tk by (xa)(ab) in Equation (1). As a result, the last occurrence of x is one position further left than it was at the start.
Case III tk−1 = (ca),where c ≠x,a.
Then tk−1 tk = (ca)(xa)
But (ca)(xa) = (xc)(ca)
We replace tk−1 tk by (xa)(bc) in Equation (1), as in Case II.
Case IV tk−1 = (bc), where b ≠ x, a and c ≠ x, a
Then tk−tk = (bc)(xa)
But (bc)(xa) = (xa)(bc)
We replace tk−1 tk by (xa)(bc) in Equation (1), as in Cases II and III.
In Case I, we are done. In Cases II, III, and IV, we repeat the argument one or more times. Each time, the last appearance of χ is one position further left than the time before. This must eventually lead to Case I. For otherwise, we end up with the last (hence the only) appearance of x being in t1.This cannot be: for if t1 = (xa) and x does not appear in t2, …, tm, then ε (x) = a, which is impossible! ■
(The box ■ is used to mark the ending of a proof.)
Our conclusion is contained in the next theorem.
Theorem 3 If π ∈ Sn, then π cannot be both an odd permutation and an even permutation.
Suppose π can be written as the product of an even number of transpositions, and differently as the product of an odd number of transpositions. Then the same would be true for π−1 But ε = π° π−1: thus, writing π−1 as a product of an even number of transpositions and π as a product of an odd number of transpositions, we get an expression for ε as a product of an odd number of transpositions. This is impossible by Theorem 2.
The set of all the even permutations in Sn is a subgroup of Sn. It is denoted by An, and is called the alternating group on the set {1, 2, …, n}.
EXERCISES
A. Practice in Multiplying and Factoring Permutations
1 Compute each of the following products in S9. (Write your answer as a single permutation.)
(a) (145)(37)(682)
(b) (17)(628)(9354)
(c) (71825)(36)(49)
(d) (12)(347)
# (e) (147)(1678)(74132)
(f) (6148)(2345)(12493)
2 Write each of the following permutations in s9 as a product of disjoint cycles:
(a)![]()
(b)![]()
(c)![]()
(d)![]()
3 Express each of the following as a product of transpositions in S8:
(a) (137428)
(b) (416)(8235)
(c) (123)(456)(1574)
(d) ![]()
4 If α = (3714), β = (123), and γ = (24135) in s7, express each of the following as a product of disjoint cycles:
(a) α−1 β
(b) γ−l α
(c) α2β
(d) β2αγ
(e) γ4
# (f) γ3α−1
(g) β−1γ
(h) α−1γ2α
(NOTE: α2 = α ∘ α, γ3 = γ ∘ γ ∘ γ, etc.)
5 In S5, write (12345) in five different ways as a cycle, and in five different ways as a product of transpositions.
6 In S5, express each of the following as the square of a cycle (that is, express as α2 where α is a cycle):
(a) (132)
(b) (12345)
(c) (13)(24)
B. Powers of
If π is any permutation, we write π ∘ π = π2, π ∘ π ∘ π = π3, etc. The convenience of this notation is evident.
1 Compute α−1, α2, α3, α4, α5 where
(a) α = (123)
(b) α = (1234)
(c) α = (123456).
In the following problems, let α be a cycle of length s, say α = (α1α2 …αs).
# 2 Describe all the distinct powers of α. How many are there? Note carefully the connection with addition of integers modulo s (page 27).
3 Find the inverse of a, and show that α−1 = αs
Prove each of the following:
# 4 α2 is a cycle iff s is odd.
5 If s is odd, α is the square of some cycle of length α. (Find it. HINT: Show α = αs+1.)
6 If s is even, say s = 2t, then α2 is the product of two cycles of length t. (Find them.)
7 If s is a multiple of k, say s = kt, then αk is the product of k cycles of length t.
8 If s is a prime number, every power of α is a cycle.
C. Even and Odd Permutations
1 Determine which of the following permutations is even, and which is odd.
(a) ![]()
(b) (71864)
(c) (12)(76)(345)
(d) (1276)(3241)(7812)
(e) (123)(2345)(1357)
Prove each of the following:
2 (a) The product of two even permutations is even.
(b) The product of two odd permutations is even.
(c) The product of an even permutation and an odd permutation is odd.
3 (a) A cycle of length l is even if l is odd.
(b) A cycle of length l is odd if l is even.
4 (a) If α and β are cycles of length / and ra, respectively, then aß is even or odd depending on whether l + m − 2 is even or odd.
(b) If π = β1 … βr where each βi is a cycle of length li, then π is even or odd depending on whether l1 + l2 + … + lr − r is even or odd.
D. Disjoint Cycles
In each of the following, let α and β be disjoint cycles, say
α = (a1a2 … as) and β = (b1b2 … br)
Prove parts 1−3:
1 For every positive integer n, (αβ)n = αnβn.
2 If αβ = ε, then α = ε and β = ε.
3 If (αβ)t = ε, then αt = ε and βt = ε (where t is any positive integer). (Use part 2 in your proof.)
4 Find a transposition γ such that αβγ is a cycle.
5 Let γ be the same transposition as in the preceding exercise. Show that ay β and γαβ are cycles.
6 Let α and β be cycles of odd length (not disjoint). Prove that if a2 = β2, then α = β.
† E. Conjugate Cycles
Prove each of the following in Sn:
1 Let α = (a1, …, as) be a cycle and let π be a permutation in Sn. Then παπ−1 is the cycle (π(a1), …, π(as)).
If α is any cycle and π any permutation, παπ−1 is called a conjugate of α. In the following parts, let π denote any permutation in Sn.
# 2 Conclude from part 1: Any two cycles of the same length are conjugates of each other.
3 If α and β are disjoint cycles, then παπ−1 and πβπ−1 are disjoint cycles.
4 Let σ be a product α1 … αt of t disjoint cycles of lengths l1 …, lt, respectively. Then πσπ−1 is also a product of t disjoint cycles of lengths l1, …, lt
5 Let α1 and α2 be cycles of the same length. Let β1 and β2 be cycles of the same length. Let α1 and β1 be disjoint, and let α2 and β2 be disjoint. There is a permutation π ∈ Sn such that α1β1 = πα2β2π−1
† F. Order of Cycles
1 Prove in Sn: If α = (a1 … as) is a cycle of length s, then αs = ε, α2s = ε, and α3s = ε. Is αk = ε for any positive integer k < s? (Explain.)
If α is any permutation, the least positive integer n such that αn = ε is called the order of α.
2 Prove in Sn: If α = (α1 … as) is any cycle of length s, the order of α is s.
3 Find the order of each of the following permutations:
(a) (12)(345)
(b) (12)(3456)
(c) (1234)(56789)
4 What is the order of αβ, if a and β are disjoint cycles of lengths 4 and 6, respectively? (Explain why. Use the fact that disjoint cycles commute.)
5 What is the order of αβ if α and β are disjoint cycles of lengths r and s, respectively? (Venture a guess, explain, but do not attempt a rigorous proof.)
† G. Even/Odd Permutations in Subgroups of Sn
Prove each of the following in Sn :
1 Let α1, …, αr be distinct even permutations, and β an odd permutation. Then α1β, …, αr β are r distinct odd permutations. (See Exercise C2.)
2 If β1, …,βr are distinct odd permutations, then β1βl, β1β2, …, βlβr are r distinct even permutations.
3 In Sn, there are the same number of odd permutations as even permutations. (HINT: Use part 1 to prove that the number of even permutations ≤ is the number of odd permutations. Use part 2 to prove the reverse of that inequality.)
4 The set of all the even permutations is a subgroup of Sn. (It is denoted by An and is called the alternating group on n symbols.)
5 Let H be any subgroup of Sn. H either contains only even permutations, or H contains the same number of odd as even permutations. (Use parts 1 and 2.)
† H. Generators of An and Sn
Remember that in any group G, a set S of elements of G is said to generate G if every element of G can be expressed as a product of elements in S and inverses of elements in S. (See page 47.)
1 Prove that the set T of all the transpositions in Sn generates Sn.
# 2 Prove that the set T1 = {(12), (13), …, (1n)} generates Sn.
3 Prove that every even permutation is a product of one or more cycles of length 3. [HINT: (13)(12) = (123); (12)(34) = (321)(134).] Conclude that the set U of all cycles of length 3 generates An.
4 Prove that the set U1 = {(123), (124), …,(12n)} generates An. [HINT: (abc) = (1ca)(1ab), (1ab) = (1b2)(12a)(12b), and (1b2) = (12b)2.]
5 The pair of cycles (12) and (12 ··· n) generates Sn. [HINT: (1 ··· n)(12)(1… n)−1 = (23); (12)(23)(12) = (13).]