A Book of Abstract Algebra, Second Edition (1982)
Chapter 6. FUNCTIONS
The concept of a function is one of the most basic mathematical ideas and enters into almost every mathematical discussion. A function is generally defined as follows: If A and B are sets, then a function from A to B is a rule which to every element x in A assigns a unique element y in B. To indicate this connection between x and y we usually write y = f(x), and we call y the image of x under the function f.
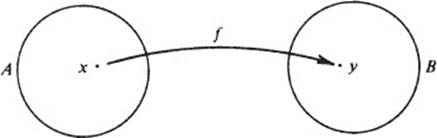
There is nothing inherently mathematical about this notion of function. For example, imagine A to be a set of married men and B to be the set of their wives. Let f be the rule which to each man assigns his wife. Then f is a perfectly good function from A to B; under this function, each wife is the image of her husband. (No pun is intended.)
Take care, however, to note that if there were a bachelor in A then f would not qualify as a function from A to B; for a function from A to B must assign a value in B to every element of A, without exception. Now, suppose the members of A and B are Ashanti, among whom polygamy is common; in the land of the Ashanti, f does not necessarily qualify as a function, for it may assign to a given member of A several wives. If/is a function from A to B, it must assign exactly one image to each element of A.
If f is a function from A to B it is customary to describe it by writing
f : A → B
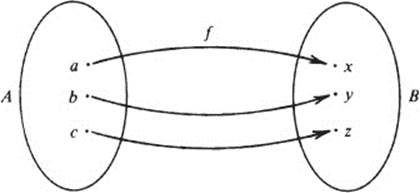
The set A is called the domain of f. The range of f is the subset of B which consists of all the images of elements of A. In the case of the function illustrated here, {a, b, c} is the domain of f, and {x, y} is the
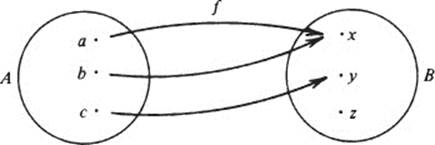
range of f(z is not in the range of f). Incidentally, this function f may be represented in the simplified notation
This notation is useful whenever A is a finite set: the elements of A are listed in the top row, and beneath each element of A is its image.
It may perfectly well happen, if f is a function from A to B, that two or more elements of A have the same image. For example, if we look at the function immediately above, we observe that a and b both have the same image x. If f is a function for which this kind of situation does not occur, then f is called an injective function. Thus,
Definition 1 A function f : A → B is called injective if each element of B is the image of no more than one element of A.
The intended meaning, of course, is that each element y in B is the image of no two distinct elements of A. So if
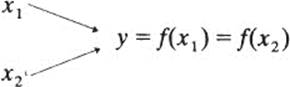
that is, xl and x2 have the same image y, we must require that xl be equal to x2. Thus, a convenient definition of “injective” is this: a function f : A →B is injective if and only if
f(x1) = f(x2) impliesx1 = x2
If f is a function from A to B, there may be elements in B which are not images of elements of A. If this does not happen, that is, if every element of B is the image of some element of A, we say that f is surjective.
Definition 2 A function f : A → B is called surjective if each element of B is the image of at least one element of A.
This is the same as saying that B is the range of f.
Now, suppose that f is both injective and surjective. By Definitions 1 and 2, each element of B is the image of at least one element of A, and no more than one element of A. So each element of B is the image of exactly oneelement of A. In this case, f is called a bijective function, or a one-to-one correspondence.
Definition 3 A function f : A →B is called bijective if it is both injective and surjective.
It is obvious that under a bijective function, each element of A has exactly one “partner” in B and each element of B has exactly one partner in A.
The most natural way of combining two functions is to form their “composite.” The idea is this: suppose f is a function from A to B, and g is a function from B to C. We apply f to an element x in A and get an element y in B; then we apply g to y and get an element z in C. Thus, z is obtained from x by applying f and g in succession. The function which
consists of applying f and g in succession is a function from A to C, and is called the composite of f and g. More precisely,
Let f : A → B and g : B → C be functions. The composite function denoted by g ∘ f is a function from A to C defined as follows:
[g ∘ f](x) = g(f(x)) for every x ∊ A
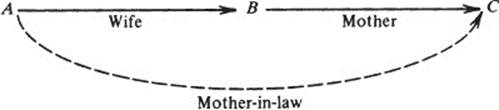
For example, consider once again a set A of married men and the set B of their wives. Let C be the set of all the mothers of members of B. Let f : A →B be the rule which to each member of A assigns his wife, and g : B → C the rule which to each woman in B assigns her mother. Then g ∘ f is the “mother-in-law function,” which assigns to each member of A his wife’s mother:
For another, more conventional, example, let f and g be the following functions from 
to : f(x) = 2x; g(x) = x + 1. (In other words, f is the rule “multiply by 2” and g is the rule “add 1.”) Their composites are the functions g ∘ fand f ∘ g given by
[f ∘ g](x) = f(g(x)) = 2(x + 1)
and
[g ∘ f](x) = g(f(x)) = 2x + 1
f ∘ g and g ∘ f are different: f ∘ g is the rule “add 1, then multiply by 2,” whereas g ∘ fis the rule “multiply by 2 and then add 1.”
It is an important fact that the composite of two injective functions is injective, the composite of two surjective functions is surjective, and the composite of two bijective functions is bijective. In other words, if f : A → B and g : B → C are functions, then the following are true:
If f and g are injective, then g ∘ f is injective.
If f and g are surjective, then g ∘ f is surjective.
If f and g are bijective, then g ∘ f is bijective.
Let us tackle each of these claims in turn. We will suppose that f and g are injective, and prove that g ∘ fis injective. (That is, we will prove that if [g ∘ f](x) = [g ∘ f](y), then x = y.)
Suppose [g ∘ f](x) = [g ∘ f](y), that is,
g(f(x)) = g(f(y))
Because g is injective, we get
f(x) = f(y)
and because f is injective,
x = y
Next, let us suppose that f and g are surjective, and prove that g ∘ f is surjective. What we need to show here is that every element of C is g ∘ f of some element of A. Well, if z ∈ C, then (because g is surjective) x = g(y) for some y ∈ B; but f is surjective, so y = f(x) for some x ∈ A. Thus,
z = g(y) = g(f(x)) = [g ∘ f](x)
Finally, if f and g are bijective, they are both injective and surjective. By what we have already proved, g ∘ f is injective and surjective, hence bijective.
A function f from A to B may have an inverse, but it does not have to. The inverse of f, if it exists, is a function f−1 (“ f inverse”) from B to A such that
x = f−1(y) if and only if y = f(x)
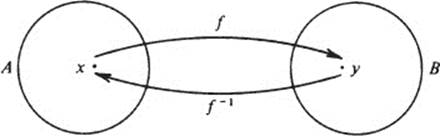
Roughly speaking, if f carries x to y then f−l carries y to x. For instance, returning (for the last time) to the example of a set A of husbands and the set B of their wives, if f : A → B is the rule which to each husband assigns his wife, then f−l : B → A is the rule which to each wife assigns her husband:
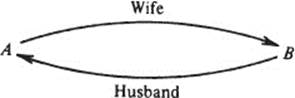
If we think of functions as rules, then f−1 is the rule which undoes what ever f does. For instance, if f is the real-valued function f(x) = 2x, then f−1 is the function f−1(x) = x/2 [or, if preferred, f−1(y) = y/2]. Indeed, the rule “divide by 2” undoes what the rule “multiply by 2” does.
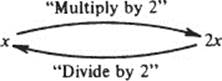
Which functions have inverses, and which others do not? If f, a function from A to B, is not injective, it cannot have an inverse; for “not injective” means there are at least two distinct elements x1 and x2 with the same image y;
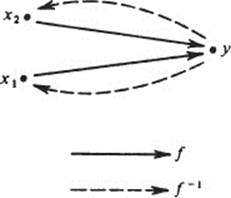
Clearly, x1 = f−1(y) and x2 = f−1(y) so f−l(y) is ambiguous (it has two different values), and this is not allowed for a function.
If f, a function from A to B is not surjective, there is an element y in B which is not an image of any element of A; thus f−l(y) does not exist. So f−1 cannot be a function from B (that is, with domain B) to A.
It is therefore obvious that if f−l exists, f must be injective and surjective, that is, bijective. On the other hand, if f is a bijective function from A to B, its inverse clearly exists and is determined by the rule that if y = f(x) then f−1(y) = x.
Furthermore, it is easy to see that the inverse of f is also a bijective function. To sum up:
A function f : A → B has an inverse if and only if it is bijective.
In that case, the inverse f−l is a bijective function from B to A.
EXERCISES
A. Examples of Injective and Surjective Functions
Each of the following is a function f : → . Determine
(a) whether or not f is injective, and
(b) whether or not f is surjective.
Prove your answer in either case.
Example 1 f(x) = 2x
f is injective.
PROOF Suppose f(a) = f(b), that is,
2a = 2b
Then
a = b
Therefore f is injective. ■
f is surjective.
PROOF Take any element y ∈. Then y = 2(y/2) = f(y/2).
Thus, every y ∈ is equal to f(x) for x = y/2.
Therefore f is surjective. ■
Example 2 f(x) = x2
f is not injective.
PROOF By exhibiting a counterexample: f(2) = 4 f(−2), although 2 ≠ −2.■
f is not surjective.
PROOF By exhibiting a counterexample: −1 is not equal to f(x) for any x ∈.■
1f(x) = 3x + 4
2f(x) = x3 + 1
3f(x) = |x|
# 4f(x) = x3 − 3x
5
# 6
7Determine the range of each of the functions in parts 1 to 6.
B. Functions on and 
Determine whether each of the functions listed in parts 1−4 is or is not (a) injective and (b) surjective. Proceed as in Exercise A.
1f : →(0, ∞), defined by f(x) = ex.
2f : (0,1)→, defined by f(x) = tan x.
3f : →, defined by f(x) = the least integer greater than or equal to x.
4f : →, defined by 
5Find a bijective function f from the set of the integers to the set E of the even integers.
C. Functions on Arbitrary Sets and Groups
Determine whether each of the following functions is or is not (a) injective and (b) surjective. Proceed as in Exercise A.
In parts 1 to 3, A and B are sets, and A × B denotes the set of all the ordered pairs (x,y) as x ranges over A and y over B.
1f : A × B → A,defined by f(x,y) = x.
2f : A × B → B × A, defined by f(x, y) = (y, x).
3f : A × B,defined by f(x) = (x, b), where b is a fixed element of B.
4G is a group, a ∈ G, and f : G → G is defined by f(x) = ax.
5G is a group and f : G → G is defined by f(x) = x−1.
6G is a group and f : G → G is defined by f(x) = x2.
D. Composite Functions
In parts 1−3 find the composite function, as indicated.
1f : → is defined by f(x) = sin x.
g : → is defined by g(x) = ex.
Find f ∘ g and g ∘ f.
2A and B are sets; f: A × B → B × A is given by f(x, y) = (y, x).
g : B × A → B is given by g(y, x) = y.
Find g ∘ f.
3f : (0,1)→ is defined by f(x) = 1 /x.
g : → is defined by g(x) = In x.
Find g ∘ f. Explain why f ∘ g is undefined.
4In school, Jack and Sam exchanged notes in a code f which consists of spelling every word backwards and interchanging every letter s with t. Alternatively, they use a code g which interchanges the letters a with o, i with u, e with y, and s with t. Describe the codes f ∘ g and g ∘ f. Are they the same?
5A = {a, b, c, d}; f and g are functions from A to A; in the tabular form described on page 57, they are given by
Give f ∘ g and g ∘ f in the same tabular form.
6G is a group, and a and b are elements of G.
f : G → G is defined by f(x) = ax.
g : G → G is defined by g(x) = bx.
Find f ∘ g and g ∘ f.
7Indicate the domain and range of each of the composite functions you found in parts 1 to 6.
E. Inverses of Functions
Each of the following functions f is bijective. Describe its inverse.
1 f : (0, ∞)→ (0, ∞), defined by f(x) = 1 /x.
2 f : → (0, ∞), defined by f(x) = ex.
3 f : →, defined by f(x) = x3 + 1.
4 f : →, defined by 
5 A = {a, b, c, d}, B = {1, 2, 3, 4} and f : A → B is given by
6 G is a group, a ∈ G, and f: G → G is defined by f(x) = ax.
F. Functions on Finite Sets
1 The members of the U.N. Peace Committee must choose, from among themselves, a presiding officer of their committee. For each member x, let f(x) designate that member’s choice for officer. If no two members vote alike, what is the range of f?
2 Let A be a finite set. Explain why any injective function f : A → A is necessarily surjective. (Look at part 1.)
3 If A is a finite set, explain why any surjective function f : A → A is necessarily injective.
4 Are the statements in parts 2 and 3 true when A is an infinite set? If not, give a counterexample.
# 5 If A has n elements, how many functions are there from A to A? How many bijective functions are there from A to A?
G. Some General Properties of Functions
In parts 1 to 3, let A, B, and C be sets, and let f : A → B and g : B → C be functions.
1 Prove that if g ∘ f is injective, then f is injective.
2 Prove that if g ∘ f is surjective, then g is surjective.
3 Parts 1 and 2, together, tell us that if g ∘ f is bijective, then f is injective and g is surjective. Is the converse of this statement true: If xy0 is injective and g surjective, is g ∘ f bijective? (If “yes,” prove it; if “no,” give a counterexample.)
4 Let f : A → B and g : B → A be functions. Suppose that y = f(x) iff x = g(y). Prove that f is bijective, and g = f−1
H. Theory of Automata
Digital computers and other electronic systems are made up of certain basic control circuits. Underlying such circuits is a fundamental mathematical notion, the notion of finite automata, also known as finite-state machines.
A finite automaton receives information which consists of sequences of symbols from some alphabet A. A typical input sequence is a word x = x1x2 … xn, where xl x2,. . . are symbols in the alphabet A. The machine has a set of internal components whose combined state is called the internal state of the machine. At each time interval the machine “reads” one symbol of the incoming input sequence and responds by going into a new internal state: the response depends both on the symbol being read and on the machine’s present internal state. Let S denote the set of internal states; we may describe a particular machine by specifying a function α : S × A → S. If si is an internal state and aj is the symbol currently being read, then α(si aj) = sk is the machine’s next state. (That is, the machine, while in state si responds to the symbol aj by going into the new state sk.) The function α is called the next-state function of the machine.
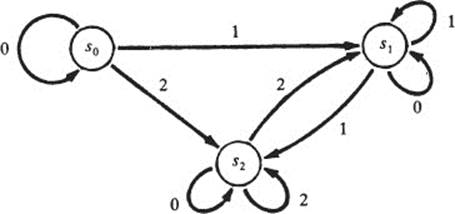
Example Let M1 be the machine whose alphabet is A = {0,1}, whose set of internal states is S = {s0, s1}, and whose next-state function is given by the table
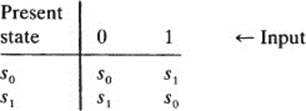
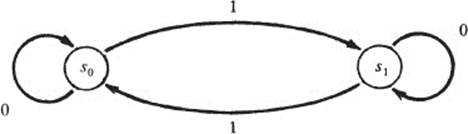
(The table asserts: When in state s0 and reading 0, remain in s0. When in s0 and reading 1, go to state s1. When in s1 and reading 0, remain in s1 When in s1 and reading 1, go to state s0.)
A possible use of M1 is as a parity-check machine, which may be used in decoding information arriving on a communication channel. Assume the incoming information consists of sequences of five symbols, 0s and Is, such as 10111. The machine starts off in state s0. It reads the first digit, 1, and as dictated by the table above, goes into state s1. Then it reads the second digit, 0, and remains in s1. When it reads the third digit, 1, it goes into state s0, and when it reads the fourth digit, 1, it goes into s1. Finally, it reaches the last digit, which is the parity-check digit: if the sum of the first four digits is even, the parity-check digit is 0; otherwise it is 1. When the parity-check digit, 1, is read, the machine goes into state s0. Ending in state s0 indicates that the parity-check digit is correct. If the machine ends in s1, this indicates that the parity-check digit is incorrect and there has been an error of transmission.
A machine can also be described with the aid of a state diagram, which consists of circles interconnected by arrows: the notation
means that if the machine is in state si when x is read, it goes into state sj. The diagram of the machine M1 of the previous example is
In parts 1−4 describe the machines which are able to carry out the indicated functions. For each machine, give the alphabet A, the set of states S, and the table of the next-state function. Then draw the state diagram of the machine.
# 1 The input alphabet consists of four letters, a, b, c, and d. For each incoming sequence, the machine determines whether that sequence contains exactly three a’s.
2 The same conditions pertain as in part 1, but the machine determines whether the sequence contains at least three a’s.
3 The input alphabet consists of the digits 0, 1, 2, 3, 4. The machine adds the digits of an input sequence; the addition is modulo 5 (see page 27). The sum is to be given by the machine’s state after the last digit is read.
4 The machine tells whether or not an incoming sequence of 0s and Is ends with 111.
5 If M is a machine whose next-state function is α, define ᾱ as follows: If x is an input sequence and the machine (in state si.) begins reading x, then ᾱ(si, x) is the state of the machine after the last symbol of x is read. For instance, if M1 is the machine of the example given above, then ᾱ(s0,11010) = s1.(The machine is in s0 before the first symbol is read; each 1 alters the state, but the 0s do not. Thus, after the last 0 is read, the machine is in state s1.)
(a) For the machine M1, give ᾱ(s0,x) for all three-digit sequences x.
(b) For the machine of part 1, give ᾱ(si, x) for each state si and every two-letter sequence x.
6 With each input sequence x we associate a function Tx: S→ S called a state transition function, defined as follows:
Tx(si) = ᾱ(si,x)
For the machine M1 of the example, if x = 11010, Tx is given by
Tx(s0) = s1 and Tx(s1)= s0
(a) Describe the transition function Tx for the machine M1 and the following sequences: x = 01001, x =10011, x = 01010.
(b) Explain why M1 has only two distinct transition functions. [Note: Two functions f and g are equal if f(x) = g(x) for every x; otherwise they are distinct.]
(c) For the machine of part 1, describe the transition function T1 for the following x: x = abbca, x = babac, x = ccbaa.
(d) How many distinct transition functions are there for the machine of part 3?
I. Automata, Semigroups, and Groups
By a semigroup we mean a set A with an associative operation. (There does not need to be an identity element, nor do elements necessarily have inverses.) Every group is a semigroup, though the converse is clearly false. With every semigroup A we associate an automaton M = M (A) called the automaton of the semigroup A. The alphabet of M is A, the set of states also is A, and the next-state function is α(s, a) = sa [or α(s, a) = s + a if the operation of the semigroup is denoted additively].
1 Describe M(4). That is, give the table of its next-state function, as well as its state diagram.
2 Describe M(S3).
If M is a machine and S is the set of states of M, the state transition functions of M (defined in Exercise H6 of this chapter) are functions from S to S. In the next exercise you will be asked to show that Ty ∘ Tx = Txy; that is, the composite of two transition functions is a transition function. Since the composition of functions is associative [f ∘ (g ∘ h) = (f ∘ g) ∘ h], it follows that the set of all transition functions, with the operation °, is a semigroup. It is denoted by 
(M) and called the semigroup of the machine M.
3 Prove that Txy = Ty ∘ Tx.
4 Let M1 be the machine of the example in Exercise H above. Give the table of the semigroup (M1. Does (M1) have an identity element? Is 
(M1) a group?
5 Let M2 be the machine of Exercise H3. How many distinct functions are there in (M3)? Give the table of (M3). Is (M3) a group? (Why?)
6 Find the table of (M) if M is the machine whose state diagram is
