ACT Math For Dummies (2011)
Part III. Digging In to Intermediate Algebra and Coordinate Geometry
Chapter 8. Coordinating a Path through Coordinate Geometry
In This Chapter
![]() Knowing the basics of graphing
Knowing the basics of graphing
![]() Graphing linear and quadratic functions
Graphing linear and quadratic functions
![]() Understanding transformations of functions on the xy-graph
Understanding transformations of functions on the xy-graph
![]() Handling higher-order polynomials and circles
Handling higher-order polynomials and circles
Coordinate geometry focuses on graphing functions and other equations on the xy-graph. Your study of graphing probably began in Algebra I when you plotted points and lines. Then you continued your graphing training in Algebra II with a more detailed look at linear and quadratic equations.
Lots of ACT questions center on graphing, so in this chapter you get up to speed on this important topic. You begin with a quick review of the basics of the xy-graph, and then you move on to the linear function — any equation that is graphed as a straight line. I also show you how to use the midpoint formula and the distance formula and how to find the slope of a line. The main event is using the slope-intercept form of the linear function, y = mx + b,to answer ACT questions.
Next, you spend some time working with quadratic functions, which take the form y = ax2 + bx + c. I show you some basic qualitative analysis of this function so you can spot its main features easily. I also give you formulas for the axis of symmetry and the vertex. After that, you discover how to work with basic transformation of functions, such as reflections, vertical shifts, and horizontal shifts. To wrap up, I touch on higher-order polynomials and circles. Whew! You have lots to cover. You better get started.
Reviewing Some Basics of Coordinate Geometry
Coordinate geometry occurs on the xy-graph (also called the coordinate plane or the Cartesian plane), on which each point is assigned a unique pair of coordinates (x, y). Coordinates are identified with a pair of axes — the x-axis and the y-axis. The two axes are essentially a pair of number lines that cross at (0, 0), a point that’s also called the origin.
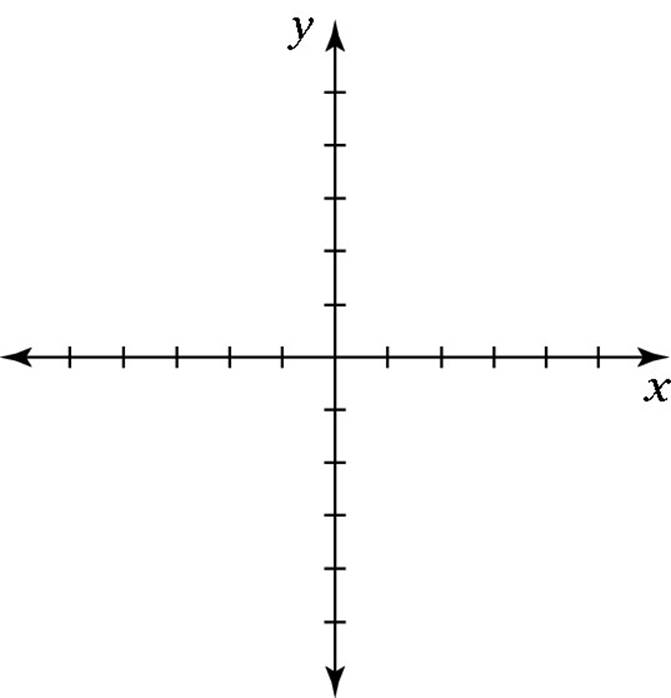
Figure 8-1 shows the basic xy-graph with a few points plotted. Each point is identified by a pair of coordinates that includes both an x-value and a y-value, respectively. When plotting a point, start at the origin, find the x-value on the x-axis as you would with a number line, and then count either up (positive) or down (negative) to find the y-value.
Figure 8-1: Thexy-graph is the basis for coordinate geometry.
Graphing Linear Functions
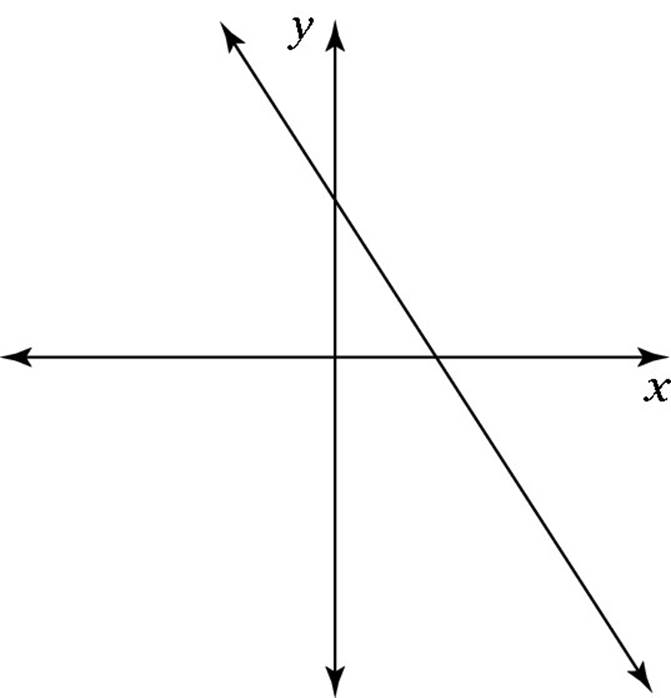
A linear function is simply a line on the xy-graph. As in plane geometry (which I discuss in Chapter 10), a line is uniquely defined by two points and extends infinitely in both directions. Graphically, a linear function is a straight line extending infinitely in both directions, as shown in Figure 8-2.
Figure 8-2: A linear function is a straight line.
Linear functions are common on the ACT, so understanding them well is important. In this section, I give you the basic skills you need to answer the most common types of ACT questions that involve lines on a graph — whether or not the question actually includes a graph. Flip to Chapter 9 for practice answering questions that use these skills.
Lining up some line segment skills
Two useful formulas for answering ACT questions on coordinate geometry are the midpoint formula and the distance formula. Both of these formulas provide information about a line segment on a graph between any two points ![]() and
and ![]() . In this section, I show you how to use both of these formulas.
. In this section, I show you how to use both of these formulas.
Finding coordinates with the midpoint formula
The midpoint formula allows you to find the coordinates of the midpoint of a line segment between any two points ![]() and
and ![]() . Here’s the formula:
. Here’s the formula:
![]()
![]() Here’s a little trick to remember the midpoint formula: Notice that for each coordinate it’s simply an application of the formula for the mean average of two numbers — the sum of two numbers divided by 2. (For more on finding the mean average, flip to Chapter 4.)
Here’s a little trick to remember the midpoint formula: Notice that for each coordinate it’s simply an application of the formula for the mean average of two numbers — the sum of two numbers divided by 2. (For more on finding the mean average, flip to Chapter 4.)
![]() In the following graph, N is on
In the following graph, N is on ![]() , equidistant from J and K. Which of the following are the coordinates of N?
, equidistant from J and K. Which of the following are the coordinates of N?
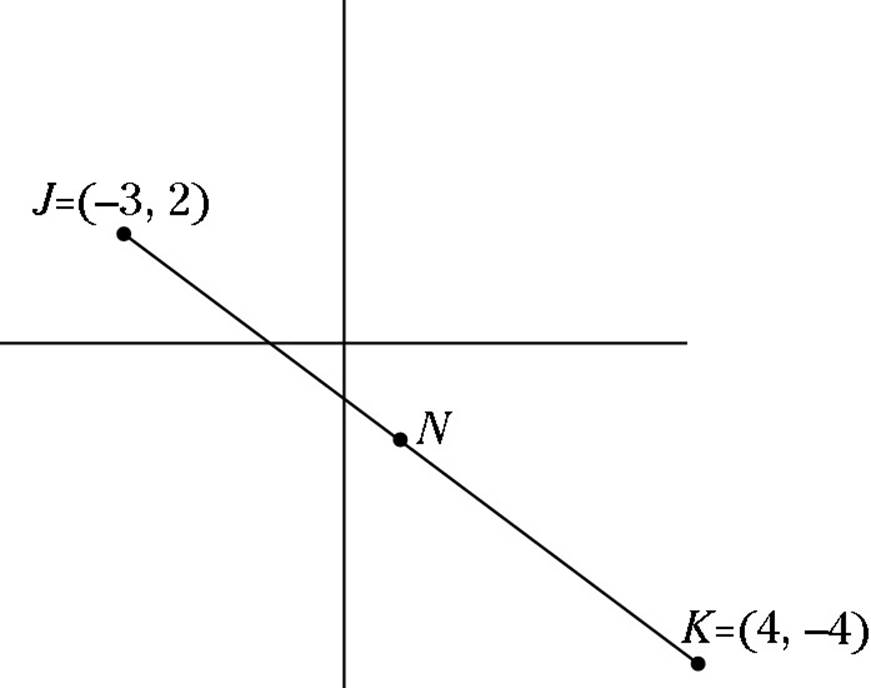
(A) (1, –1)
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Plug the four values for the coordinates of J and K into the midpoint formula to get your answer:
![]()
As you can see, the correct answer is Choice (C).
Going the whole ten yards with the distance formula
The distance formula allows you to find the length of a line segment between any two points ![]() and
and ![]() . Consider the formula:
. Consider the formula:
![]()
![]() The distance formula looks complicated, but it’s really just an application of the Pythagorean theorem. To show the similarity between the two, I’ll tweak the formula slightly by squaring both sides of it:
The distance formula looks complicated, but it’s really just an application of the Pythagorean theorem. To show the similarity between the two, I’ll tweak the formula slightly by squaring both sides of it:
![]()
Now notice that ![]() and
and ![]() are the lengths of the two legs of a triangle with a hypotenuse that’s the line segment you want to measure:
are the lengths of the two legs of a triangle with a hypotenuse that’s the line segment you want to measure:
c2 = a2 + b2
![]() In the following figure, what is the length of
In the following figure, what is the length of ![]() ?
?
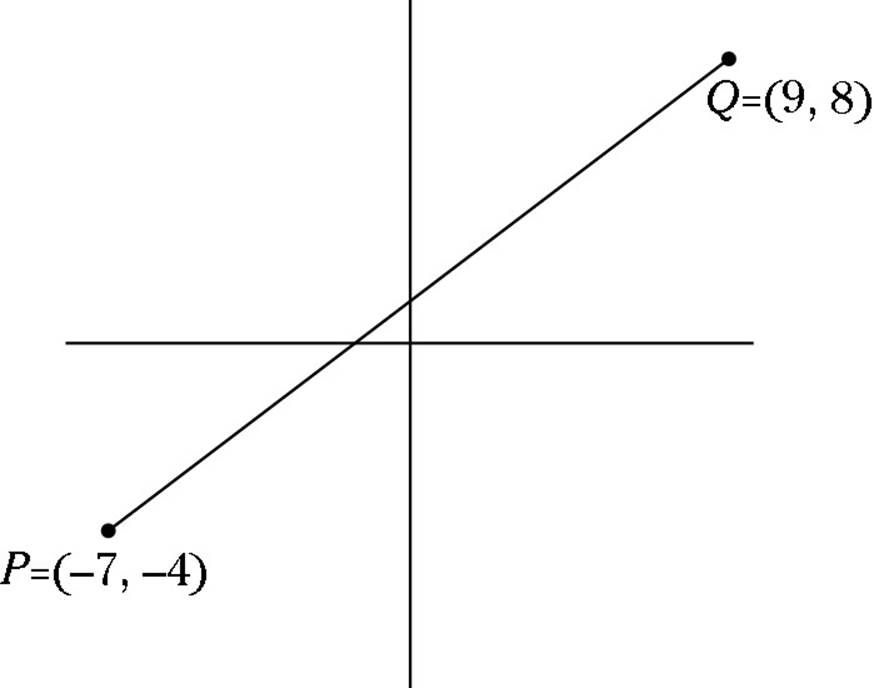
(A) 17
(B) 18
(C) 20
(D) 21
(E) 24
Plug the four values into the distance formula:
![]()
Simplify:
![]()
Therefore, the correct answer is Choice (C).
Measuring the slope of a line
The slope of a line is a measurement of how quickly the line rises or falls as it goes from left to right. When you’re working with a graph, the quickest way to measure the slope is with the rise-run slope formula:
![]()
Find the rise and the run as follows:
![]() The rise is the number of steps up or down from one point to the next.
The rise is the number of steps up or down from one point to the next.
• When going up, the rise is a positive number.
• When going down, the rise is a negative number.
![]() The run is the number of steps from left to right from one point to the next. (The run is always a positive number.)
The run is the number of steps from left to right from one point to the next. (The run is always a positive number.)
Table 8-1 provides a cheat sheet for evaluating the slope of a line.
Table 8-1 Evaluating the Slope of a Line
|
When the Slope of a Line Is: |
The Line (from Left to Right) Is: |
|
A positive number |
Rising |
|
A negative number |
Falling |
|
0 |
Horizontal |
|
No slope |
Vertical |
![]() According to the following graph, which of the answer choices has a slope that is an integer?
According to the following graph, which of the answer choices has a slope that is an integer?
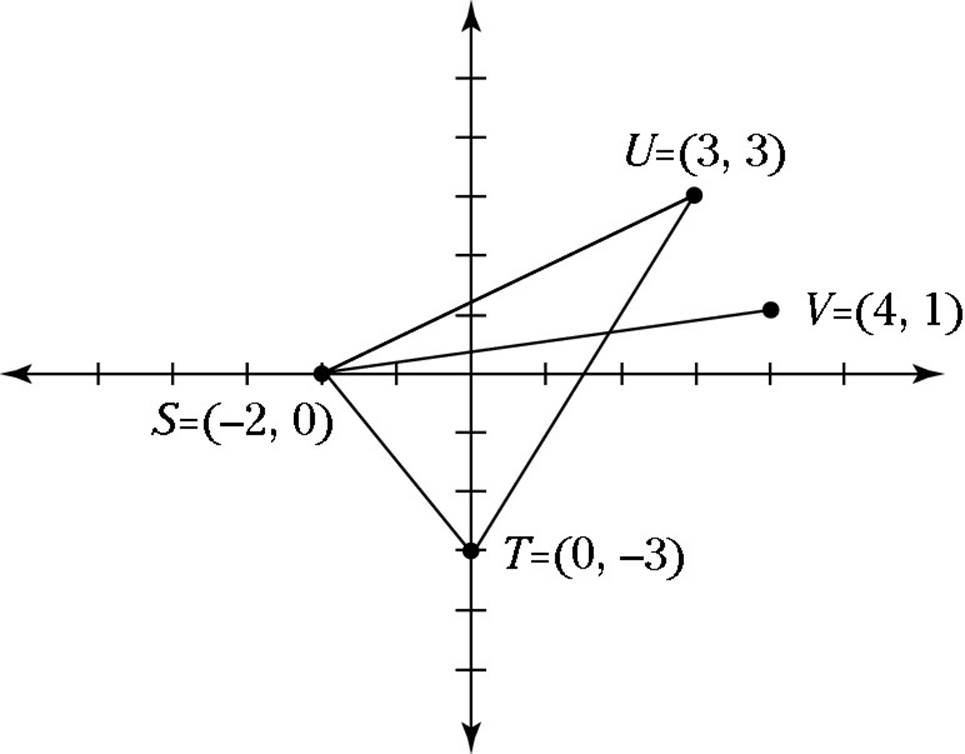
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) None of these has a slope that’s an integer.
Recall from Chapter 4 that an integer is a whole number that’s either positive or negative (or 0). Use the rise-run formula to calculate the slopes of these lines until you find the one whose slope is an integer, or show that none of them is an integer:

The correct answer is Choice (D).
Using the rise-run formula can be difficult when you aren’t provided a graph of the line you’re working with. In these cases, you can use the two-point slope formula. This formula allows you to calculate the slope of any line that includes the points ![]() and
and ![]() . Here’s the formula:
. Here’s the formula:
![]()
![]() Notice that in this formula, the y-values go on top and the x-values on the bottom — don’t mix them up!
Notice that in this formula, the y-values go on top and the x-values on the bottom — don’t mix them up!
![]() What is the slope of a line that contains the points (–5, 1) and (7, 10)?
What is the slope of a line that contains the points (–5, 1) and (7, 10)?
(F) ![]()
(G) ![]()
(H) ![]()
(J) ![]()
(K) ![]()
Plug these values into the formula for slope:
![]()
Thus, the correct answer is Choice (G).
Applying the slope-intercept form
The most useful form for a linear equation is the slope-intercept form:
y = mx + b
This form contains the two variables x and y, with y isolated on the left side of the equal sign. It also includes two constants represented by the letters m and b, each of which provides information about the line:
![]() The constant m is the slope of the line. For example, in the equation y = –3x + 5, the slope of the line is –3.
The constant m is the slope of the line. For example, in the equation y = –3x + 5, the slope of the line is –3.
![]() The constant b is the y-intercept of the line. The y-intercept is the point at which the line intersects the y-axis. For example, in the equation y = –3x + 5, the y-intercept of the line is 5. In other words, the line includes the point (0, 5).
The constant b is the y-intercept of the line. The y-intercept is the point at which the line intersects the y-axis. For example, in the equation y = –3x + 5, the y-intercept of the line is 5. In other words, the line includes the point (0, 5).
![]() You can use the slope-intercept form to help answer virtually every ACT question that involves a line on a graph. If a linear equation isn’t given in the slope-intercept form, use algebra to put it in this form.
You can use the slope-intercept form to help answer virtually every ACT question that involves a line on a graph. If a linear equation isn’t given in the slope-intercept form, use algebra to put it in this form.
![]() What is the slope of a line whose equation is 3x + 2y = 7?
What is the slope of a line whose equation is 3x + 2y = 7?
(A) 3
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Begin by putting the equation in the slope-intercept form:
![]()
In this equation, the slope is ![]() , so the correct answer is Choice (C).
, so the correct answer is Choice (C).
You can use the slope-intercept form in conjunction with the formula for slope that I show you in the earlier section “Measuring the slope of a line.” The following example shows you how.
![]() Which of the following is the equation of a line that has a y-intercept of –4 and goes through the point (1, –2)?
Which of the following is the equation of a line that has a y-intercept of –4 and goes through the point (1, –2)?
(F) y = x – 4
(G) y = 2x – 4
(H) y = –2x – 4
(J) ![]()
(K) ![]()
Remember that the y-intercept is simply a point on the line with an x-coordinate of 0. Because this line has a y-intercept of –4, this point is (0, –4). Plug this point and the point (1, –2) into the formula for slope:
![]()
When you know both the slope (m = 2) and the y-intercept (b = –4), you can write the equation in slope-intercept form:
![]()
So the correct answer is Choice (G).
You also can use the slope-intercept form to answer trickier questions (I told you this form would come in handy). Use the information provided in the problem to find the equation of the line, and then answer the question. The following example walks you through a question like this one.
![]() Which of the following is the equation of a line that includes the point (10, –1) and has a slope of
Which of the following is the equation of a line that includes the point (10, –1) and has a slope of ![]() ?
?
(A) –x + 10y = 3
(B) 10x – y = 5
(C) 3x + 5y = 9
(D) 3x – 5y = 35
(E) –3x + 5y = 7
To answer this question, you want to use the slope-intercept form, so you need to know the values of m and b. You’re given the slope, so m = ![]() . To find the value of b, plug in the information from the point that’s given (x = 10 and y = –1), and then simplify and solve for b:
. To find the value of b, plug in the information from the point that’s given (x = 10 and y = –1), and then simplify and solve for b:
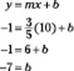
When you know the values of both m and b, you can write the equation for the line in the slope-intercept form:
![]()
Now use algebra to put this equation into the form you need to answer the question:
![]()
Therefore, the correct answer is Choice (D).
Working with parallel and perpendicular lines
Some ACT questions provide parallel or perpendicular lines on a graph. Remember the following information for when you’re dealing with these types of questions:
![]() Parallel lines always have the same slope. For example, any line parallel to
Parallel lines always have the same slope. For example, any line parallel to ![]() also has a slope of
also has a slope of ![]() .
.
![]() Perpendicular lines always have slopes that are negative reciprocals of each other. To find the negative reciprocal, turn the fraction upside down and negate it. For example, any line perpendicular to
Perpendicular lines always have slopes that are negative reciprocals of each other. To find the negative reciprocal, turn the fraction upside down and negate it. For example, any line perpendicular to ![]() has a slope of
has a slope of![]() .
.
![]() What is the equation of a line that has an x-intercept of –3 and is parallel to y = 3x – 9?
What is the equation of a line that has an x-intercept of –3 and is parallel to y = 3x – 9?
(A) y = 3x + 3
(B) y = 3x – 3
(C) y = 3x + 9
(D) y = –3x – 3
(E) y = –3x – 9
The line you’re looking for is parallel to y = 3x – 9, so it also has a slope of 3. Thus, you can rule out Choices (D) and (E). It has an x-intercept of –3, which is the point (–3, 0). Plug these values into the slope-intercept form and solve for b, as I show you in the earlier section “Applying the slope-intercept form.” Here’s what your work should look like:
y = mx + b
0 = 3(–3) + b
0 = –9 + b
9 = b
Now that you know both the slope and the y-intercept for this line, you can write the equation in the slope-intercept form:
y = mx + b
y = 3x + 9
The correct answer is Choice (C).
![]() What is the equation of a line that passes through the point (0, 3) and is perpendicular to y = 8x + 5?
What is the equation of a line that passes through the point (0, 3) and is perpendicular to y = 8x + 5?
(F) y = 8x
(G) y = 8x + 3
(H) ![]()
(J) ![]()
(K) ![]()
This line you’re looking for is perpendicular to y = 8x + 5, so its slope is the negative reciprocal of 8. In other words, ![]() . Thus, you can rule out Choices (F) and (G). You could plug this value, along with x = 0 and y = 3, into the slope-intercept form to find b, but you can use an even easier way. Notice that (0, 3) is the y-intercept, so b = 3. Plug in these values directly:
. Thus, you can rule out Choices (F) and (G). You could plug this value, along with x = 0 and y = 3, into the slope-intercept form to find b, but you can use an even easier way. Notice that (0, 3) is the y-intercept, so b = 3. Plug in these values directly:
![]()
So the correct answer is Choice (J).
Giving Your Quads a Workout: Graphing Quadratic Functions
A quadratic function is any function in the following form:
y = ax2 + bx + c
When you graph a quadratic function on the xy-plane, the result is a parabola — a curved shape extending infinitely in both directions, as shown in Figure 8-3.
Figure 8-3: A quadratic function is graphed as a parabola.
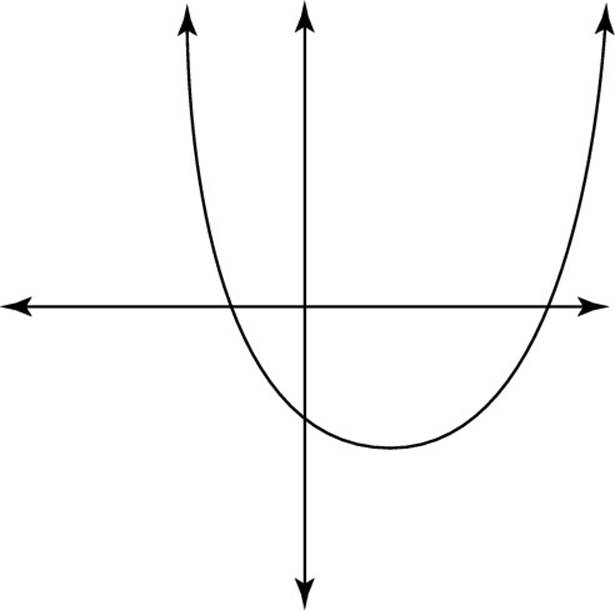
The quadratic equation, ax2 + bx + c = 0, which you encounter in Chapter 7, is a form of the quadratic function in which y = 0. In this section, I show you everything you need to know to successfully graph quadratic functions.
![]() If you have a graphing calculator, such as the TI-83 or TI-89, you can use it to graph quadratic functions. For more details, pick up TI-83 Plus Graphing Calculator For Dummies by C.C. Edwards (Wiley) or TI-89 Graphing Calculator For Dummies by C.C. Edwards (Wiley).
If you have a graphing calculator, such as the TI-83 or TI-89, you can use it to graph quadratic functions. For more details, pick up TI-83 Plus Graphing Calculator For Dummies by C.C. Edwards (Wiley) or TI-89 Graphing Calculator For Dummies by C.C. Edwards (Wiley).
Searching for the qualities of a quadratic
Sketching a quadratic equation by plotting points can be time-consuming. If you have a graphing calculator, you can use it to graph a quadratic function. However, you can answer some ACT questions even more easily if you know a few simple tricks. Each of these tricks links the coefficients (a, b, and c) in a quadratic equation to a different quality of the parabola — that is, a general rule about how the parabola is placed on the graph. I show you the three tricks you need to know in the following sections.
Trick 1: Checking the direction of your parabola
This first trick relates to the sign of the variable a (in the term ax2):
![]() When a is positive, the graph is concave up. In other words, you can imagine pouring water in it like a cup.
When a is positive, the graph is concave up. In other words, you can imagine pouring water in it like a cup.
![]() When a is negative, the graph is concave down. In this case, the cup is upside-down.
When a is negative, the graph is concave down. In this case, the cup is upside-down.
This trick is especially helpful when a question gives you the graph of a parabola, because it’s easy to see at a glance which direction it’s facing.
![]() Which of the following equations CANNOT be the graph of the function shown here?
Which of the following equations CANNOT be the graph of the function shown here?
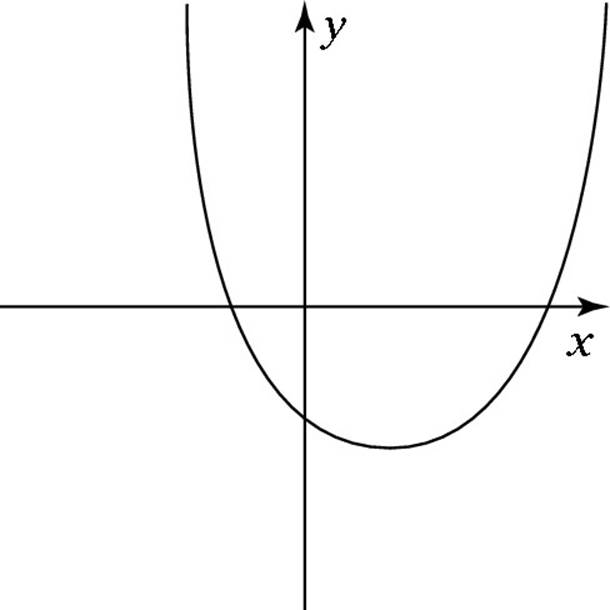
(A) y = –x2 – x – 1
(B) y = 100x2 – 1000x – 100
(C) y = 0.01x2 – 0.1x – 0.001
(D) ![]()
(E) ![]()
Even with a graphing calculator, graphing all five of these equations would take a long time. Fortunately, the trick I show you earlier provides a much easier way to answer the question: The parabola in the figure is concave up, so a is positive. Voila! So the equation for this graph isn’t y = –x2 – x – 1, making the correct answer Choice (A).
Trick 2: Looking at your parabola’s vertex
The second trick relates to the signs of the variables a and b (in the terms ax2 and bx):
![]() When the signs of a and b are the same (either both positive or both negative), the graph shifts to the left. That is, the vertex of the parabola is to the left of the y-axis.
When the signs of a and b are the same (either both positive or both negative), the graph shifts to the left. That is, the vertex of the parabola is to the left of the y-axis.
![]() When the signs of a and b are different (one is positive and the other is negative), the graph shifts to the right. In this case, the vertex of the parabola is to the right of the y-axis.
When the signs of a and b are different (one is positive and the other is negative), the graph shifts to the right. In this case, the vertex of the parabola is to the right of the y-axis.
![]() A good mnemonic for remembering this rule is that the word same and the word left both have four letters.
A good mnemonic for remembering this rule is that the word same and the word left both have four letters.
![]() A quadratic function y = ax2 + bx + c crosses the x axis at x = 4 and x = –2. Which of the following must be true?
A quadratic function y = ax2 + bx + c crosses the x axis at x = 4 and x = –2. Which of the following must be true?
(A) a > 0
(B) a ≥ b
(C) a ≠ b
(D) b ≠ c
(E) c < 0
At first glance, you may think this difficult question isn’t even answerable. A quick sketch shows you that lot of different parabolas could fit this description:
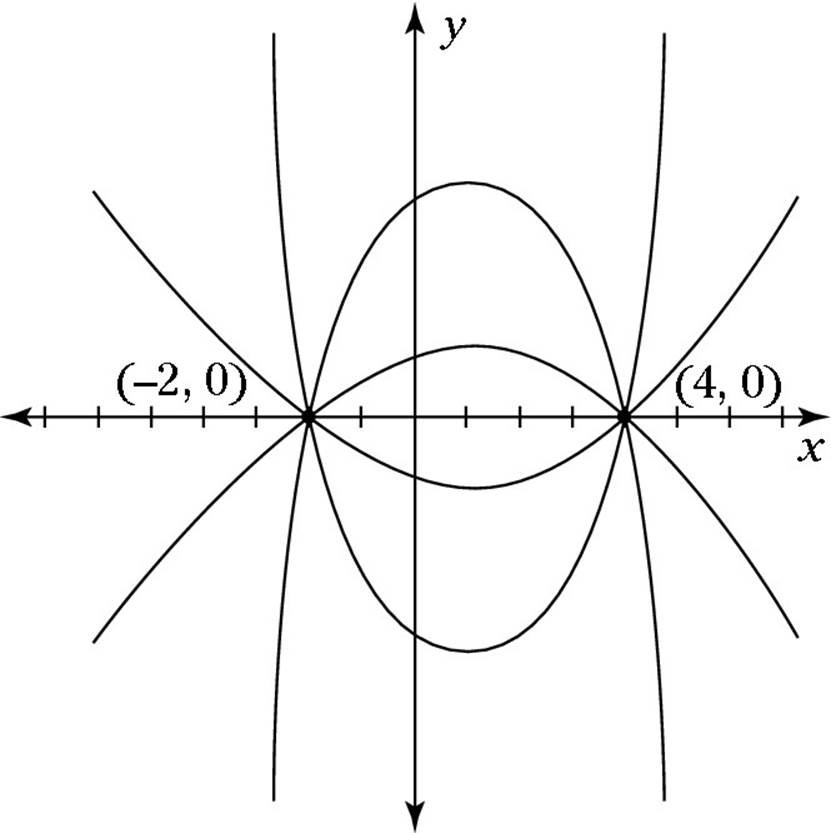
The only thing you know for sure is that the parabola’s vertex is horizontally in the middle of these two points, so it’s somewhere on the line x = 1. Thus, the parabola (whatever it looks like) is shifted to the right, so a and b have different signs. So a ≠ b, making the correct answer Choice (C).
Trick 3: Keeping an eye on variable c
The third trick relates to the sign of the variable c (the constant term of the equation). Keep the following rules in mind:
![]() When c is positive, the y-intercept is positive. In other words, the parabola intersects the y-axis above the origin.
When c is positive, the y-intercept is positive. In other words, the parabola intersects the y-axis above the origin.
![]() When c is negative, the y-intercept is negative. That is, the parabola intersects the y-axis below the origin.
When c is negative, the y-intercept is negative. That is, the parabola intersects the y-axis below the origin.
Warning: Be clear that in a quadratic function, c is the y-intercept. In contrast, in a linear function (y = mx + b), b is the y-intercept.
![]() Which of the following could be a graph of the function y = –x2 + 5x – 2?
Which of the following could be a graph of the function y = –x2 + 5x – 2?
(A) 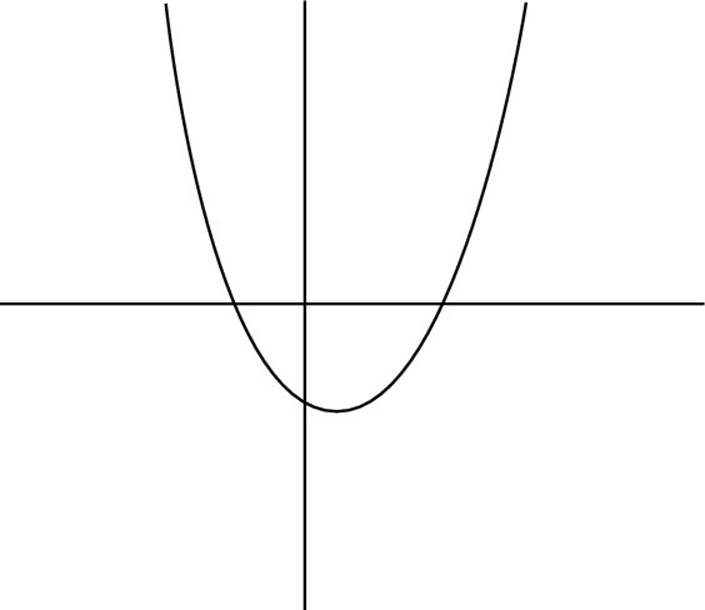
(B) 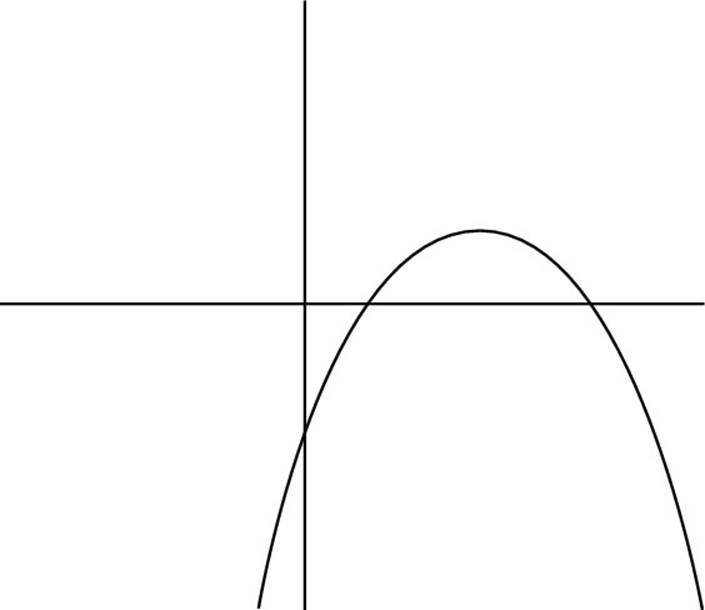
(C) 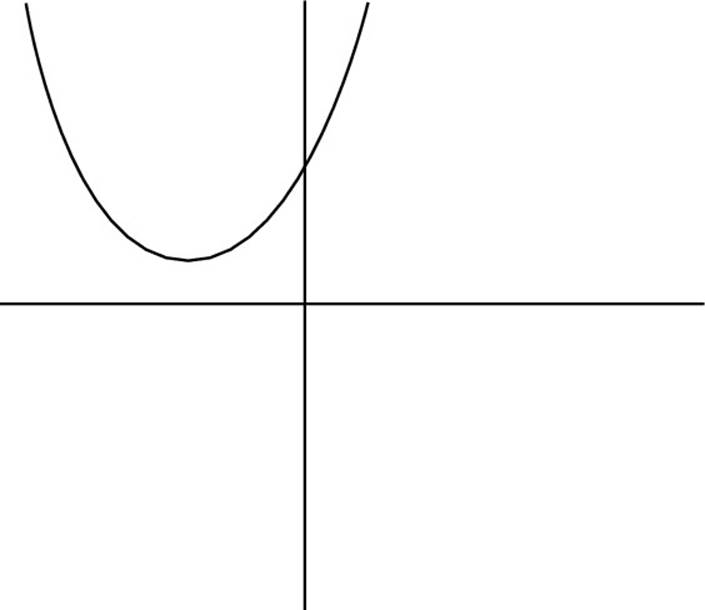
(D) 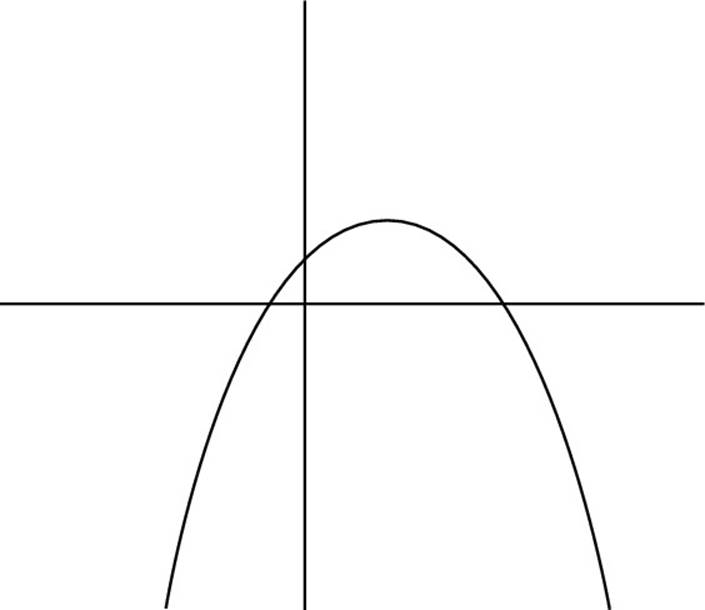
(E) 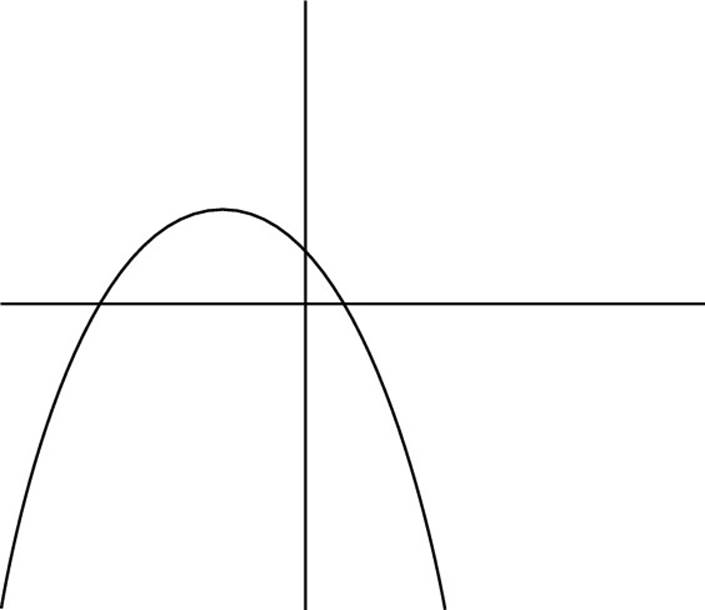
In this equation, c = –2, so the y-intercept is below the y-axis. As a result, you can rule out Choices (C), (D), and (E). Additionally, a = –1, so the parabola is concave down. So you also can rule out Choice (A), which makes the correct answer Choice (B).
Calculating two features of parabolas
Every parabola has the following two key features that you can calculate when you know the equation:
![]() The axis of symmetry: This axis is the vertical line that divides the parabola down the middle.
The axis of symmetry: This axis is the vertical line that divides the parabola down the middle.
![]() The vertex: The vertex is the lowest (or highest) point on the parabola. It’s always a point on the axis of symmetry.
The vertex: The vertex is the lowest (or highest) point on the parabola. It’s always a point on the axis of symmetry.
These two features of a parabola are easy to spot on a graph, so they can be useful when a question asks you to make a connection between the graph of a parabola and its equation.
In this section, I provide the formulas you use to find both of these features. I also show you how to apply them to answer ACT questions.
Accessing the axis of symmetry
The axis of symmetry is the vertical line that divides a parabola down the middle. For a quadratic function y = ax2 + bx + c, the formula for the axis of symmetry is
![]()
![]() The formula for the axis of symmetry explains why the signs of a and b cause the parabola to shift to the left or right. When a and b have the same sign, the axis of symmetry is negative, which shifts the parabola to the left; when they have opposite signs, the axis of symmetry is positive, shifting the parabola to the right.
The formula for the axis of symmetry explains why the signs of a and b cause the parabola to shift to the left or right. When a and b have the same sign, the axis of symmetry is negative, which shifts the parabola to the left; when they have opposite signs, the axis of symmetry is positive, shifting the parabola to the right.
![]() Which of the following lines divides the function y = 2x2 + 12x + 3 into two symmetrical parts?
Which of the following lines divides the function y = 2x2 + 12x + 3 into two symmetrical parts?
(A) x = 2
(B) x = –3
(C) x = 12
(D) y = –2
(E) y = 3
The question asks for the axis of symmetry for the function. The answer will be a vertical line, so you can rule out Choices (D) and (E). Simply plug the values of a = 2 and b = 12 into the formula to calculate the axis of symmetry:
![]()
Therefore, the correct answer is Choice (B).
Changing direction at the vertex
The vertex of a parabola is the point where the parabola changes directions. It’s always either the lowest or the highest point on the parabola. Here’s the formula for the coordinates of the vertex for the quadratic function y = ax2+ bx + c:
![]()
![]() This formula can be useful but difficult to remember. To help yourself remember, notice that the x-coordinate is simply the x value of the axis of symmetry, which I discuss in the earlier section “Accessing the axis of symmetry.” The y-coordinate looks complicated, but you may recall the numerator b2 – 4ac as the part of the quadratic equation (see Chapter 7) that’s inside the square root.
This formula can be useful but difficult to remember. To help yourself remember, notice that the x-coordinate is simply the x value of the axis of symmetry, which I discuss in the earlier section “Accessing the axis of symmetry.” The y-coordinate looks complicated, but you may recall the numerator b2 – 4ac as the part of the quadratic equation (see Chapter 7) that’s inside the square root.
![]() In the following figure, the vertex of the parabola y = –2x2 + 3x + 1 is located at (h, k). What is the value of k?
In the following figure, the vertex of the parabola y = –2x2 + 3x + 1 is located at (h, k). What is the value of k?
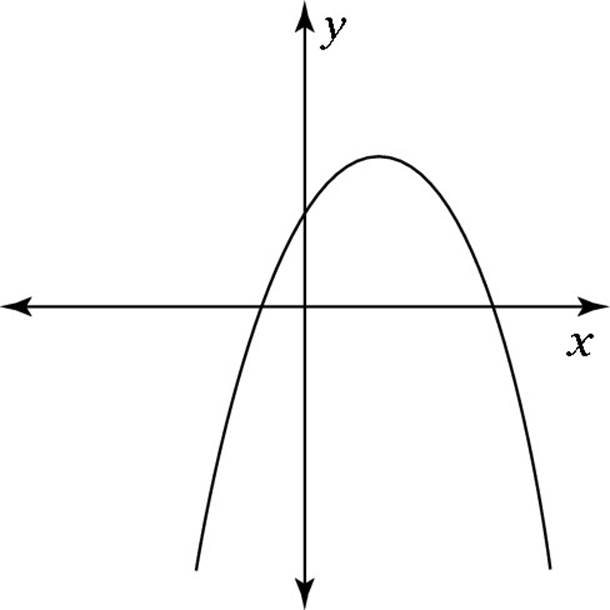
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
The question asks you for the value of k, which is the y-coordinate of the vertex. Plug a = –2, b = 3, and c = 1 into the formula to find the value:
![]()
As you can see, the correct answer is Choice (C).
Solving and graphing quadratic inequalities
A quadratic inequality resembles a quadratic equation, but the equal sign is replaced by one of the four inequality signs (<, >, ≤, or ≥). To solve a quadratic inequality, you solve it as a quadratic equation, as I discuss in Chapter 7, and then graph it as a quadratic function. Finally, you use the graph to answer the question. This process makes a lot more sense with an example.
![]() If x2 – 7x + 12 < 0, then one possible value of x is
If x2 – 7x + 12 < 0, then one possible value of x is
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(E) ![]()
Begin by solving the related quadratic equation:
x2 – 7x + 12 = 0
(x – 3)(x – 4) = 0
Now split into two equations and solve both:
x – 3 = 0 x – 4 = 0
x = 3 x = 4
At this point, a bit of graphing helps. The two values of x (in this case, 3 and 4) also are called zeros of the equation, because the graph of the function y = x2 – 7x + 12 crosses the x-axis at these points. Additionally, the parabola is concave up because the x2 term is positive. These two facts enable you to sketch a graph that’s useful for answering the question:
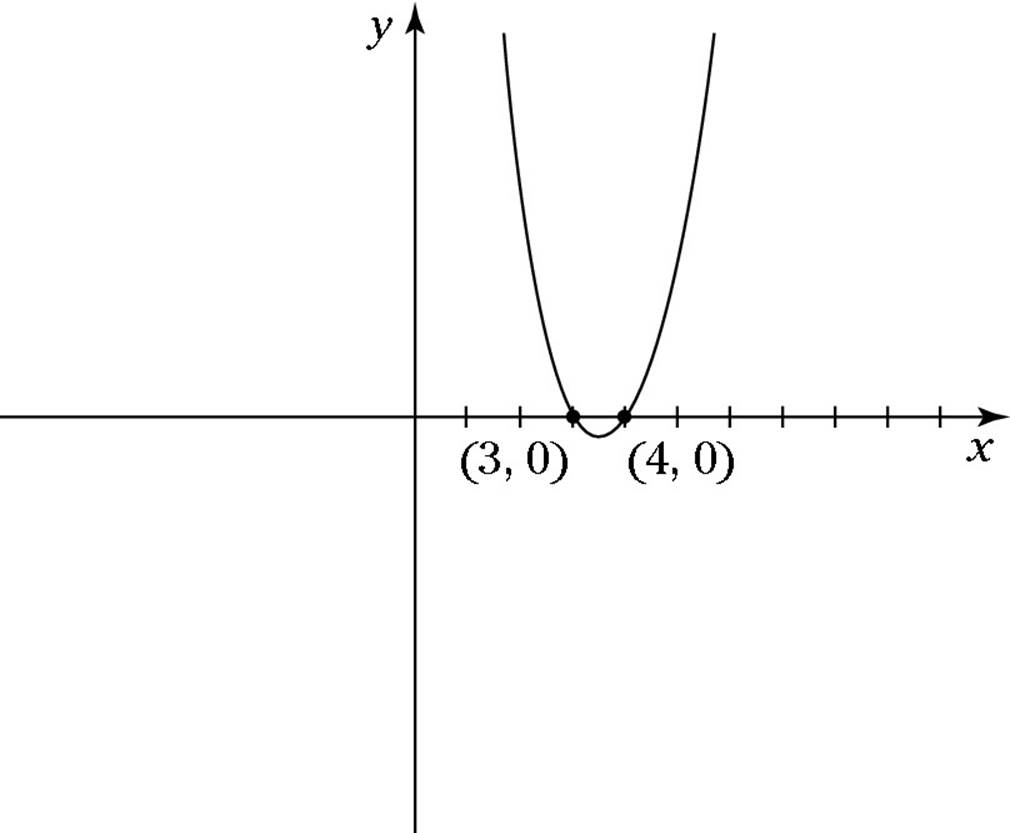
The inequality x2 – 7x + 12 < 0 holds true wherever the graph is below the x-axis — that is, when 3 < x < 4. Therefore, the inequality is true when ![]() . So the correct answer is Choice (B).
. So the correct answer is Choice (B).
Recognizing Three Transformations
A transformation is a small change to a function that alters the graph of that function in a predictable way. The transformations you’re likely to see on the ACT come in three varieties: reflections, vertical shifts, and horizontal shifts. In this section, I show you how to work with all three of these transformations.
Reversing graphs with reflections
A reflection of a function causes the graph of that function to appear reversed on the opposite side of either the x-axis or the y-axis. Here are the two types of reflections for the function y = f(x):
![]() The function y = –f(x) reflects the function y = f(x) vertically across the x-axis, negating the whole function.
The function y = –f(x) reflects the function y = f(x) vertically across the x-axis, negating the whole function.
![]() The function y = f(–x) reflects the function y = f(x) horizontally across the y-axis changing each x to –x.
The function y = f(–x) reflects the function y = f(x) horizontally across the y-axis changing each x to –x.
![]() In the following figure, f(x) = x2 + 3 and g(x) is a reflection of this function across the x-axis, so g(x) =
In the following figure, f(x) = x2 + 3 and g(x) is a reflection of this function across the x-axis, so g(x) =
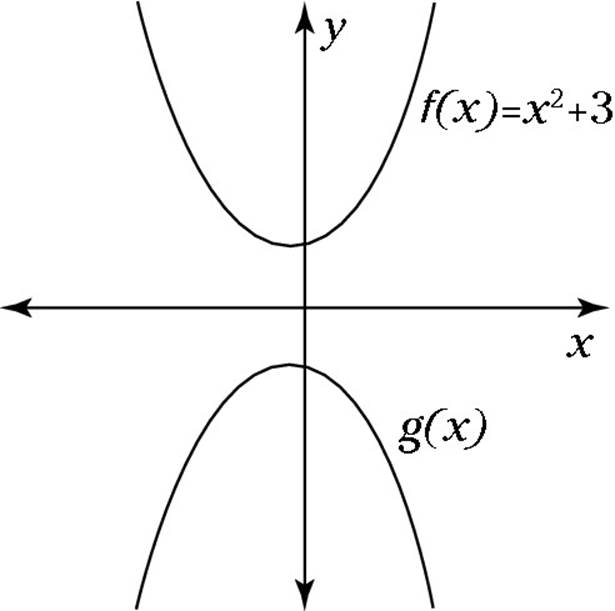
(A) x2 – 3
(B) –x2 + 3
(C) –x2 – 3
(D) (–x)2 + 3
(E) (–x)2 – 3
The function g(x) is a reflection of f(x) vertically across the x-axis. Use parentheses so you don’t get confused, and then simplify:
g(x) = –f(x) = –(x2 + 3) = –x2 – 3
As you can see, the correct answer is Choice (C).
![]() Which of the following would be a reflection of the function y = x3 – x2 horizontally across the y-axis?
Which of the following would be a reflection of the function y = x3 – x2 horizontally across the y-axis?
(F) y = x2(x + 1)
(G) y = x2(1 – x)
(H) y = –x2(x + 1)
(J) y = –x2(x – 1)
(K) y = –x2(1 – x)
To reflect y = x3 – x2 horizontally across the y-axis, change every x to –x (use parentheses to keep track of these changes) and then simplify:
y = (–x)3 – (–x)2 = –x3 – x2
To make this result resemble the answers provided, factor out –x2:
y = –x2(x + 1)
Therefore, the correct answer is Choice (H).
Movin’ on up (or down): Vertical shift
A vertical shift moves a function either up or down. Here are the two types of vertical shifts for the function y = f(x):
![]() The function y = f(x) + n vertically shifts the function up n units. Here you add n to the whole function.
The function y = f(x) + n vertically shifts the function up n units. Here you add n to the whole function.
![]() The function y = f(x) – n vertically shifts the function down n units. In other words, to shift down, you subtract n from the whole function.
The function y = f(x) – n vertically shifts the function down n units. In other words, to shift down, you subtract n from the whole function.
![]() If f(x) = x2 + 2x + 4, and g(x) shifts this function up 1 unit, which of the following equals g(x)?
If f(x) = x2 + 2x + 4, and g(x) shifts this function up 1 unit, which of the following equals g(x)?
(A) x2 + 4
(B) x2 + 2x + 3
(C) x2 + 2x + 5
(D) x2 + 4x + 5
(E) x2 + 4x + 6
To shift the function up 1 unit, just add 1 to the entire function:
g(x) = (x2 + 2x + 4) + 1 = x2 + 2x + 5
So the correct answer is Choice (C).
Shifting horizontally
A horizontal shift moves a function either to the left or to the right. Here are the two types of horizontal shifts for the function y = f(x):
![]() The function y = f(x + n) horizontally shifts the function to the left, or in the negative direction, by n units. You change each x to x + n.
The function y = f(x + n) horizontally shifts the function to the left, or in the negative direction, by n units. You change each x to x + n.
![]() The function y = f(x – n) horizontally shifts the function to the right, or in the positive direction, by n units. You change each x to x – n.
The function y = f(x – n) horizontally shifts the function to the right, or in the positive direction, by n units. You change each x to x – n.
![]() Notice that horizontal shift occurs in the opposite direction than you may think: Adding inside the parentheses moves the function in the negative direction along the x-axis.
Notice that horizontal shift occurs in the opposite direction than you may think: Adding inside the parentheses moves the function in the negative direction along the x-axis.
![]() If f(x) = 3x2 + 5x – 1, and g(x) shifts this function 2 units to the left, then g(x) =
If f(x) = 3x2 + 5x – 1, and g(x) shifts this function 2 units to the left, then g(x) =
(A) 3x2 + 5x + 1
(B) 3x2 + 5x – 3
(C) 3x2 – 7x + 1
(D) 3x2 + 17x + 1
(E) 3x2 + 17x + 21
To shift f(x) = 3x2 + 5x – 1 to the left 2 units (that is, in the negative direction), change every x to x + 2:
g(x) = 3(x + 2)2 + 5(x + 2) – 1
Now simplify to get your answer:
= 3(x2 + 4x + 4) + 5x + 10 – 1
= 3x2 + 12x + 12 + 5x + 10 – 1
= 3x2 + 17x + 21
Thus, the correct answer is Choice (E).
![]() On the xy-graph, g(x) shifts the function f(x) up 5 units and to the right 4 units. Which of the following is true?
On the xy-graph, g(x) shifts the function f(x) up 5 units and to the right 4 units. Which of the following is true?
(F) g(x) = f(x + 4) + 5
(G) g(x) = f(x + 5) + 4
(H) g(x) = f(x + 4) – 5
(J) g(x) = f(x – 4) + 5
(K) g(x) = f(x – 5) – 4
To shift the function 5 units up, add 5 to the entire function (as I show you in the earlier section “Movin’ on up (or down): Vertical shift”):
f(x) + 5
To shift the function 4 units to the right (that is, in the positive direction), change x to x – 4:
f(x – 4) + 5
The correct answer is Choice (J).
Taking on Advanced Equations
Most ACT questions that cover coordinate geometry focus on linear and quadratic equations, which I discuss earlier in this chapter. In this section, however, I touch on two advanced types of equations: polynomials and circles.
Raising the bar with higher-order polynomials
Linear functions and quadratic functions are specific examples of polynomials — functions based on raising x to the power of a positive integer. The degree of a polynomial is the highest exponent to which x is raised. Table 8-2 shows some common polynomials and the degrees to which they are raised.
Table 8-2 Common Polynomials
|
Degree |
Commonly called |
Example |
|
1st degree |
Linear equation |
y = 4x + 2 |
|
2nd degree |
Quadratic equation |
y = x2 + 5x – 6 |
|
3rd degree |
Cubic equation |
y = x3 – 3x2 – 1 |
|
4th degree |
Quartic equation |
y = 16x4 – 1 |
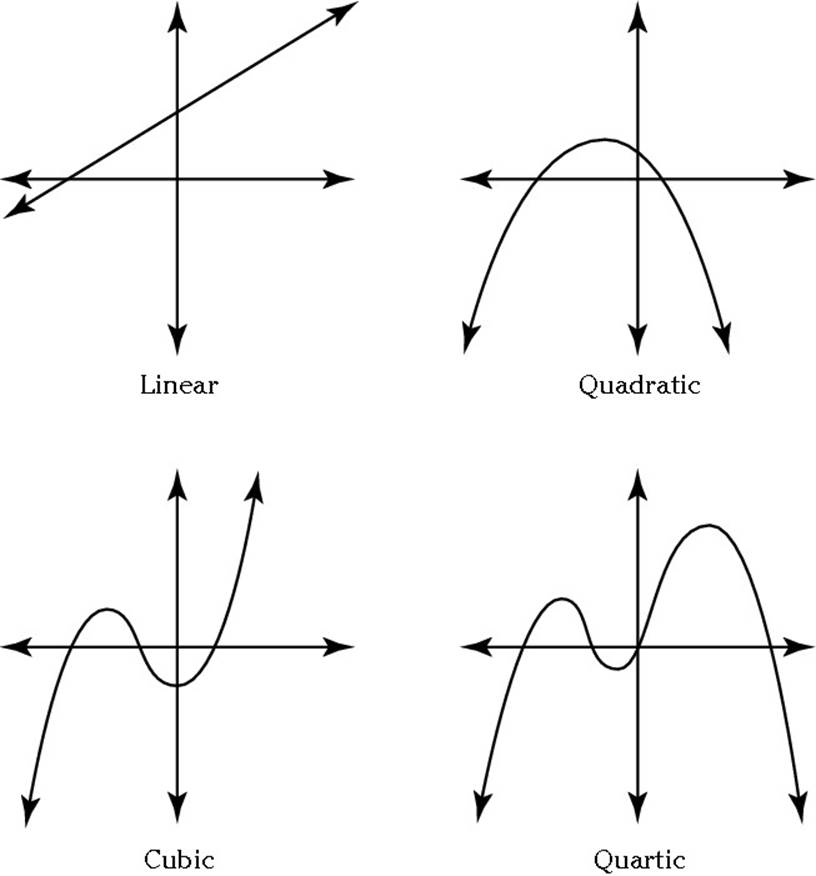
Higher-order polynomials aren’t so common on the ACT, but knowing a few basics is a good idea. Figure 8-4 shows you example graphs of basic first- through fourth-degree polynomials. The degree of a polynomial tells you the maximum number of zeros for that equation, or, in other words, the maximum number of times it can cross the x-axis.
Figure 8-4:Graphs of some common polynomials.
![]() Which of the following functions or combinations of functions CANNOT intersect with the x-axis exactly four times?
Which of the following functions or combinations of functions CANNOT intersect with the x-axis exactly four times?
(A) four linear functions
(B) a linear function and a quadratic function
(C) two quadratic functions
(D) a 4th-degree polynomial
(E) a 5th-degree polynomial
Each of the preceding functions or combination of functions can cross the x-axis exactly four times except the combination of a linear function and a quadratic function, which can cross the x-axis no more than three times. Therefore, the correct answer is Choice (B).
![]() Which of the following CANNOT be the graph of a polynomial?
Which of the following CANNOT be the graph of a polynomial?
(F) 
(G) 
(H) 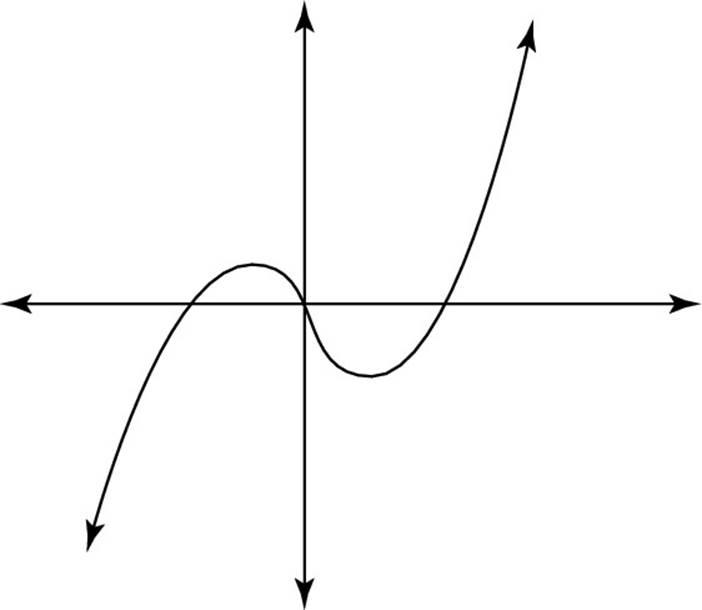
(J) 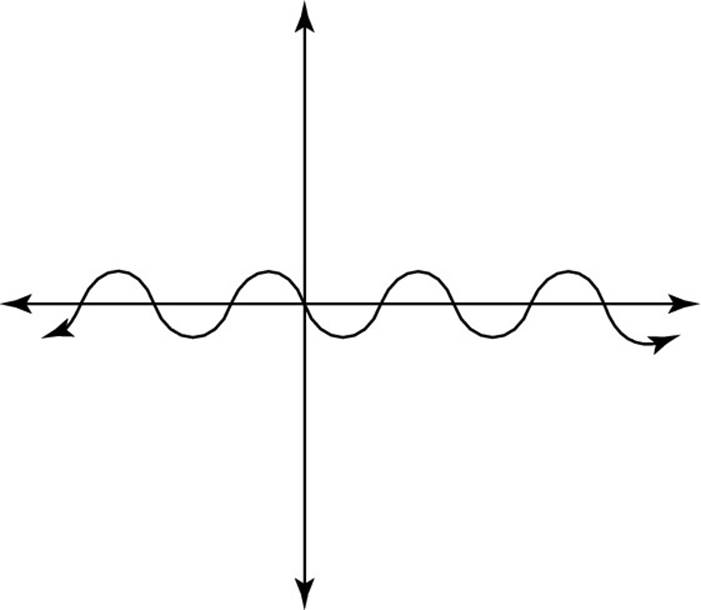
(K) 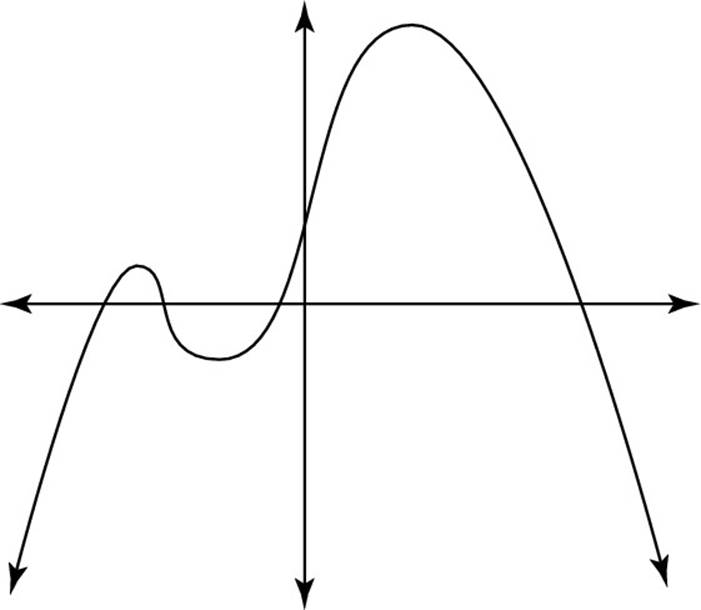
The sine curve crosses the x-axis an infinite number of times, so it can’t be a polynomial of any degree. Thus, the correct answer is Choice (J).
Going ’round and ’round with circles
Although the circle is a familiar and simple shape, it’s less commonly associated with coordinate geometry. ACT questions involving circles are rather uncommon, but they do show up from time to time. Most ACT questions focusing on circles involve a straightforward application of the basic formula I introduce in this section.
The formula for a circle of radius r centered at the point (h, k) is:
(x – h)2 + (y – k)2 = r2
For example, here’s the equation for a circle with a radius of 5 centered at (3, –4):
(x – 3)2 + (y + 4)2 = 25
Warning: Be careful not to mix up positive and negative coordinates in the formula for a circle: In this example, (x – 3)2 moves the circle along the x-axis in the positive direction, and (y + 4)2 moves it along the y-axis in thenegative direction.
![]() What is the formula for the circle shown in the following figure given that the circle has a radius of 4?
What is the formula for the circle shown in the following figure given that the circle has a radius of 4?
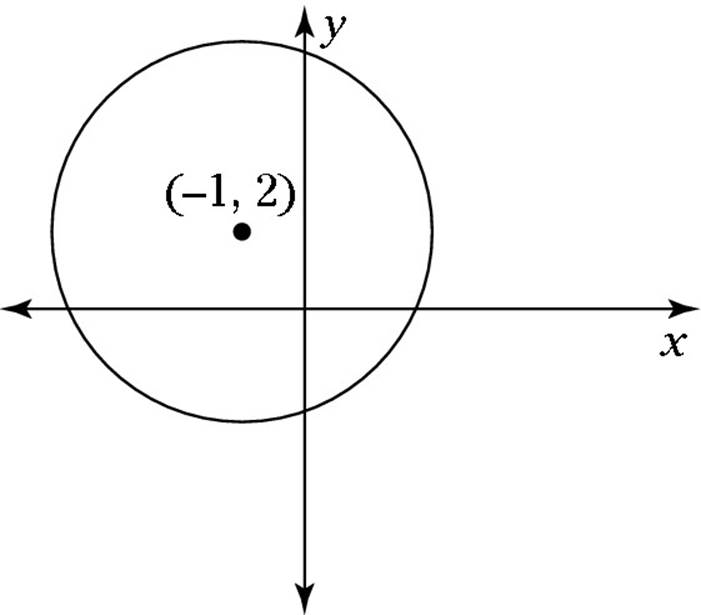
(A) (x + 1)2 + (y – 2)2 = 4
(B) (x – 1)2 + (y + 2)2 = 4
(C) (x + 1)2 + (y – 2)2 = 16
(D) (x – 1)2 + (y + 2)2 = 16
(E) (x – 1)2 + (y – 4)2 = 16
Place the values h = –1, k = 2, and r = 4 into the formula for a circle and simplify:
(x – h)2 + (y – k)2 = r2
(x – (–1))2 + (y – 2)2 = 42
(x + 1)2 + (y – 2)2 = 16
So the correct answer is Choice (C).