Advanced Calculus of Several Variables (1973)

Part IV. Multiple Integrals

Chapter 6. IMPROPER INTEGRALS AND ABSOLUTELY INTEGRABLE FUNCTIONS

Thus far in this chapter on integration, we have confined our attention to bounded functions that have bounded support. This was required by our definition of the integral of a nonnegative function as the volume of its ordinate set (if contented)—if f: ⁿ → is to be integrable, then its ordinate set must be contented. But every contented set is a priori bounded, so f must be bounded and have bounded support.

However there are certain types of unbounded subsets of ⁿ with which it is natural and useful to associate a notion of volume, and analogously functions which are either unbounded or have unbounded support, but for which it is nevertheless natural and useful to define an integral. The following two examples illustrate this.

Example 1Let f: [1, ∞) → be defined by f(x) = 1/x². Let A denote the ordinate set of f, and A_n the part of A lying above the closed interval [1, n] (Fig. 4.39). Then

Since and lim_n→∞ v(A_n) = 1, it would seem natural to say that

despite the fact that f does not have bounded support. (Of course what we really mean is that our definitions of volume and/or the integral ought to be extended so as to make this true.)

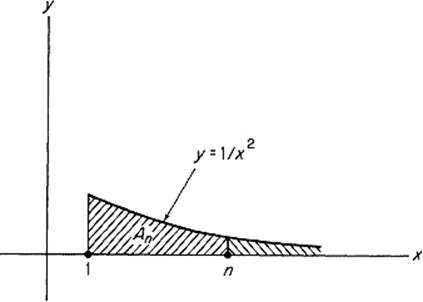
Figure 4.39

Example 2Let f be the unbounded function defined on (0, 1 ] by . Let A denote the ordinate set of f, and A_n the part of A lying above the closed interval [1/n, 1] (Fig. 4.40). Then

Since and lim_n→∞ v(A_n) = 2, it would seem natural to say that

These two examples indicate both the need for some extension (to unbounded situations) of our previous definitions, and a possible method of making this extension. Given a function f : U → , with either f or U (or both) unbounded,

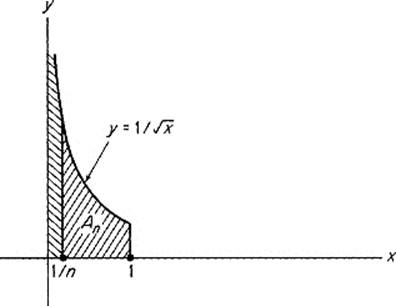
Figure 4.40

we might choose a sequence of subsets of U which “fill up” U in some appropriate sense, on each of which f is integrable, and then define

provided that this limit exists. Of course we would have to verify that ∫_U f is thereby well-defined, that is, that its value is independent of the particular chosen sequence . Partly because of this problem of well-definition, we shall formulate our initial definition of ∫_U f in a slightly different manner, and then return later to the interpretation of ∫_Uf as a sequential limit (as above).

We deal first with the necessity for f : U → to be integrable on enough subsets of U to “fill up” U. We say that f is locally integrable on U if and only if f is integrable on every compact (closed and bounded) contented subset of U. For instance the function f(x) = 1/x² of Example 1 is not integrable on (1, ∞), but is locally integrable there. Similarly the function f(x) = 1/x^½ of Example 2 is not integrable on (0, 1), but is locally integrable there.

It will be convenient to confine our attention to open domains of definition. So let f : U → be a locally integrable function on the open set . We then say that f is absolutely integrable on U if and only if, given ε > 0, there exists a compact contented subset B_ε of U such that

for every compact contented set which contains B_ε.

The student should verify that the sum of two absolutely integrable functions on U is absolutely integrable, as is a constant multiple of one, so the set of all absolutely integrable functions on U is a vector space. This elementary fact will be used in the proof of the following proposition, which provides the reason for our terminology.

Proposition 6.1If the function f : U → is absolutely integrable, then so is its absolute value f.

We will later prove the converse, so f is absolutely integrable if and only if f is.

PROOFWriting f = f⁺ − f⁻, it suffices by the above remark to show that f⁺ and f⁻ are both absolutely integrable, since f = f⁺ + f⁻. We consider f⁺. Given ε > 0, choose B_ε as in the definition, such that implies

if A is a compact contented subset of U. It will suffice to show that also implies that

Given a compact contented set A with , define

so that f(x) = f⁺(x) for , and

because f⁺(x) = 0 if . Then

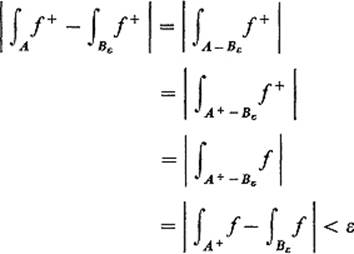
as desired, because A⁺ is a compact contented set such that .

The number I, which the following theorem associates with the absolutely integrable function f on the open set , will be called the improper (Riemann) integral of f on U. It will be temporarily denoted by I_Uf (until we have verified that I_Uf = ∫_Uf in case f is integrable on U).

The following definition will simplify the interpretation of I_Uf as a sequential limit of integrals of f on compact contented subsets of U. The sequence of compact contented subsets of U is called an approximating sequencefor U if (a) for each , and (b) .

Theorem 6.2 Suppose f is absolutely integrable on the open set . Then there exists a number I = I_Uf with the property that, given ε > 0, there exists a compact contented set C_ε such that

for every compact contented subset A of U containing C_ε. Furthermore

for every approximating sequence for U.

PROOFTo start with, we choose a (fixed) approximating sequence for U (whose existence is provided by Exercise 6.16). Given η > 0, the Heine-Borel theorem (see the Appendix) implies that if k is sufficiently large. Here B_η/2 is the compact contented subset of U (provided by the definition) such that implies that

Consequently, if k and l are sufficiently large, it follows that

Thus is a Cauchy sequence of numbers, and therefore has a limit I (see the Appendix).

Now let C_ε = B_ε/3. Given a compact contented subset A of U which contains C_ε, choose a fixed k sufficiently large that and . Then

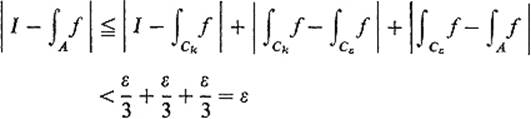
as desired. This completes the proof of the first assertion.

Now let be an arbitrary approximating sequence for U. Given δ > 0, choose K sufficiently large that , for all . Then what we have just proved gives for all , so it follows that

We can now show that I_Uf and ∫_Uf are equal when both are defined. Note that, if f is integrable on the open set , then it follows from Exercise 3.1 that f is locally integrable on U (why?).

Theorem 6.3If is open and f : U → is integrable, then f is absolutely integrable, and

PROOFLet M be an upper bound for the values of f(x) on U. Given ε > 0, let B_ε be a compact contented subset of U such that v(U − B_ε) < ε/M. If A is a compact contented subset of U which contains B_ε, then

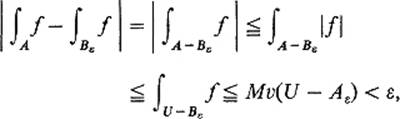
so it follows that f is absolutely integrable on U.

If in addition A contains the set C_ε of Theorem 6.2, then

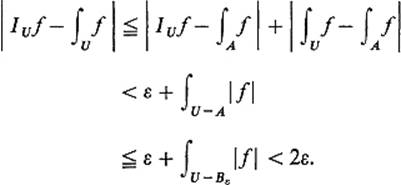
This being true for all ε > 0, it follows that I_Uf = ∫_Uf.

In order to proceed to compute improper integrals by taking limits over approximating sequences as in Theorem 6.2, we need an effective test for absolute integrability. For nonnegative functions, this is easy to provide. We say that the improper integral ∫_Uf is bounded (whether or not it exists, that is, whether or not f is absolutely integrable on U) if and only if there exists M > 0 such that

for every compact contented subset A of U.

Theorem 6.4Suppose that the nonnegative function f is locally integrable on the open set U. Then f is absolutely integrable on U if and only if ∫_Uf is bounded, in which case ∫_Uf is the least upper bound of the values ∫_Af, for all compact contented sets .

PROOFSuppose first that (1) holds, and denote by I the least upper bound of {∫_Af} for all compact contented . Given ε > 0, I − ε is not an upper bound for the numbers {∫_Af}, so there exists a compact contented set such that

If A is any compact contented set such that then, since , we have

so it follows that both

The first inequality implies that f is absolutely integrable, and then the second implies that ∫_Uf = I as desired (using Theorem 6.2).

Conversely, if f is absolutely integrable on U, then it is easily seen that for every compact contented subset U of A, so we can take M = ∫_Uf in (1).

Corollary 6.5Suppose the nonnegative function f is locally integrable on the open set U, and let be an approximating sequence for U. Then f is absolutely integrable with

provided that this limit exists (and is finite).

PROOFThe fact that the monotone increasing sequence of numbers is bounded (because it has a finite limit) implies easily that ∫_Uf is bounded, so f is absolutely integrable by Theorem 6.4. Hence (2) follows from Theorem 6.2.

As an application, we will now generalize see Examples 1 and 2 to ⁿ. Let A denote the solid annular region (Fig. 4.41), and let f be a spherically symmetric continuous function on A. That is,

for some function g, where T : ⁿ → ⁿ is the n-dimensional spherical coordinates mapping of Exercise 5.19. By part (a) of that exercise, and the change of variables theorem, we have

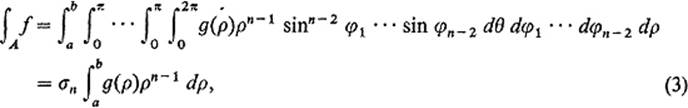
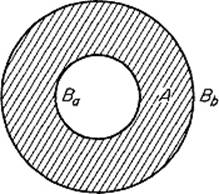
Figure 4.41

where

Example 3Let U = ⁿ − B₁ⁿ and f(x) = 1/x^p where p > n. Writing A_k = B_kⁿ − B₁ⁿ, Corollary 6.5 and (3) above give

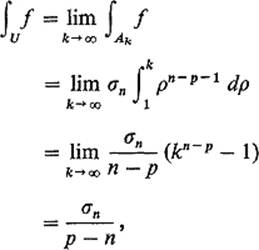
because k^n−p → 0 since n − p < 0.

Example 4Let U denote the interior of the unit ball with the origin deleted, and f(x) = 1/x^p with p < n. So now the problem is that f, rather than U, is unbounded. Writing , Corollary 6.5 and (3) give

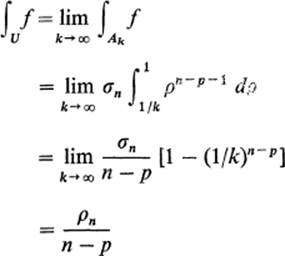
because p < n.

For nonnegative locally integrable functions, Corollary 6.5 plays in practice the role of a “working definition.” One need not worry in advance about whether the improper integral ∫_Uf actually exists (that is, whether f is absolutely integrable on U). Simply choose a convenient approximating sequence for U, and compute . If this limit is finite, then ∫_Uf does exist, and its value is the obtained limit.

In the case of an arbitrary (not necessarily nonnegative) function, one must know in advance that f is absolutely integrable on U. Once this has been established, Theorem 6.2. enables us to proceed as above—choose an approximating sequence for U, and then compute .

The simplest way to show that a given locally integrable function f : U → is absolutely integrable is to compare it with a function g : U → which is already known to be absolutely integrable, using the comparison test stated below. First we need the converse of Proposition 6.1.

Corollary 6.6Let f : U → be locally integrable. If f is absolutely integrable on U, then so is f.

PROOFWrite f = f⁺ − f⁻, so f = f⁺ + f⁻. Since f is absolutely integrable, ∫_Uf is bounded (by Theorem 6.4). It follows immediately that ∫_Uf⁺ and ∫_Uf⁻ are bounded. Hence Theorem 6.4 implies that f⁺ and f⁻ are both absolutely integrable on U, so f = f⁺ − f⁻ is also.

The import of Corollary 6.6 is that, in practice, we need only to test nonnegative functions for absolute integrability.

Corollary 6.7(Comparison Test) Suppose that f and g are locally integrable on U with . If g is absolutely integrable on U, then so is f.

PROOFSince g is absolutely integrable, ∫_Ug is bounded (by Theorem 6.4). But then the fact that implies immediately that ∫_Uf is also bounded, so f is also absolutely integrable.

Example 5 The functions

are all absolutely integrable on U = (1, ∞), by comparison with the absolutely integrable function g(x) = 1/x² of Examples 1 and 3. For the latter, we note that

so sin x/x² is absolutely integrable by Corollary 6.7. But then it follows from Corollary 6.6 that (sin x)/x² itself is absolutely integrable on (1, ∞).

Similarly the functions

are absolutely integrable on U = (0, 1), by comparison with the function g(x) = 1/x^1/2 of Examples 2 and 4.

Next we want to define a different type of improper integral for the case of functions of a single variable. Suppose that f is locally integrable on the open interval (a, b), where possibly a = − ∞ or b = + ∞ or both. We want to define the improper integral denoted by

to be contrasted with the improper integral ∫_{(a, b)}f(x) dx which is defined if f is absolutely integrable on (a, b). It will turn out that exists in some cases where f is not absolutely integrable on (a, b), but that if both exist.

The new improper integral is obtained by restricting our attention to a single special approximating sequence for (a, b), instead of requiring that the same limit be obtained for all possible choices of the approximating sequence (as, by Theorem 6.2., is the case if f is absolutely integrable). Separating the four possible cases, we define

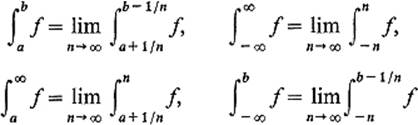
(where a and b are finite), provided that the appropriate limit exists (and is finite) and say that the integral converges; otherwise it diverges.

Example 6The integral converges, because

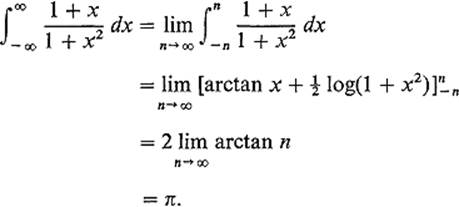
However f(x) = (1 + x)/(1 + x²) is not absolutely integrable on (− ∞, ∞) = . If it were, we would have to obtain the same limit π for any approximating sequence for . But, taking A_n = [−n, 2n], we obtain

Example 7Consider . Since lim_x→0[(sin x)/x] = 1, sin x/x is continuous on [0, 1]. So we need only consider the convergence of

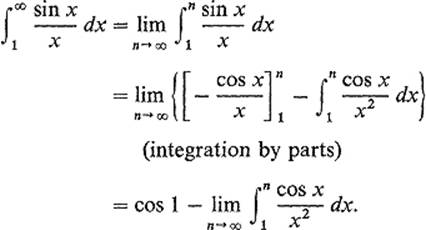
But (cos x)/x² is absolutely convergent on (1, ∞), by comparison with 1/x².

Therefore converges; its actual value is π/2 (see Exercise 6.14). However the function f(x) = (sin x)/x is not absolutely integrable on (0, ∞) (see Exercise 6.15).

The phenomenon illustrated by Examples 6 and 7, of converging despite the fact that f is not absolutely convergent on (a, b), does not occur when f is nonnegative.

Theorem 6.8Suppose f : (a, b) → is locally integrable with . Then f is absolutely integrable if and only if converges, in which case

PROOFThis follows immediately from Theorem 6.2. and Corollary 6.5.

Example 8We want to compute , which converges because , while

To obtain the value, we must resort to a standard subterfuge.

Consider f : ² → defined by . Since

when x² + y² is sufficiently large, it follows from Example 3 and the comparison test that is absolutely integrable on ². If D_n denotes the disk of radius n in ², then

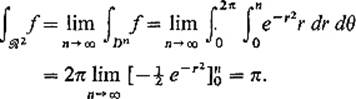
On the other hand, if S_n denotes the square with edgelength 2n centered at the origin, then

Comparing the two results, we see that

Since is an even function, it follows that

Example 9The important gamma function Γ : (0, ∞) → is defined by

We must show that this improper integral converges for all x > 0. Now

If , then f(t) = t^x−1 e^−t is continuous on [0, 1]. If , then , so the first integral on the right converges, because g(t) = t^x−1 is absolutely convergent on (0, 1) by Example 4, since 1 − x < 1.

To consider the second integral, note first that

so

for t sufficiently large. Since 1/t² is absolutely convergent on (1, ∞), it follows that converges.

The fundamental property of the gamma function is that Γ(x + 1) = xΓ(x) if x > 0:

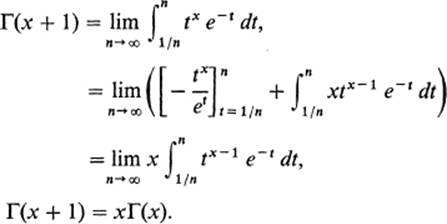
Since Γ(1) = 1, it follows easily that

if n is a positive integer (Exercise 6.1).

Example 10The beta function is a function of two variables, defined on the open first quadrant Q of the xy-plane by

If either x < 1 or y < 1 or both, this integral is improper, but can be shown to converge by methods similar to those used with the gamma function (Exercise 6.9).

Substituting t = sin² θ in (6) (before taking the limit in the improper cases), we obtain the alternative form

The beta function has an interesting relation with the gamma function. To see this, we first express the gamma function in the form

by substituting t = u² in (5). From this it follows that

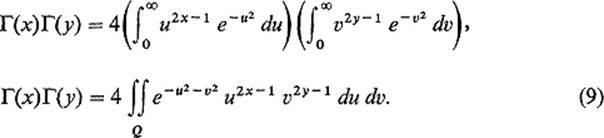
This last equality is easily verified by use of the approximating sequence for Q, where A_n = [1/n, n] × [1/n, n].

It follows from Corollary 6.5 that the integrand function in (9) is absolutely convergent, so we may use any other approximating sequence we like. Let us try , where B_n is the set of all those points with polar coordinates (r, θ) such that and (Fig. 4.42). Then

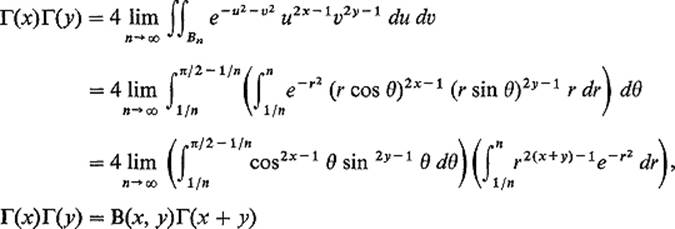
using (7) and (8) and the obvious symmetry of the beta function. Hence

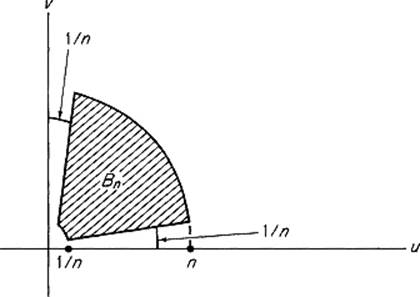
Figure 4.42

As a typical application of (7) and (10), we obtain

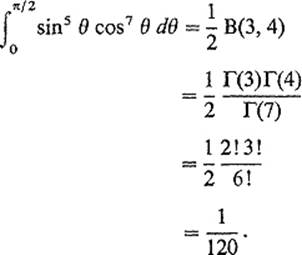
Another typical example of the use of gamma functions to evaluate integrals is

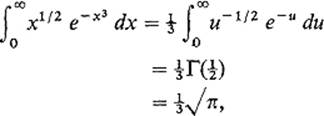
making the substitution u = x³ and using the fact that (Exercise 6.2).

Exercises

6.1Show that Γ(1) = 1, and then deduce from Γ(x + 1) = xΓ(x) that Γ(n + 1) = n!.

6.2Show that . Hint: Substitute t = u² in the integral defining , and refer to Example 8. Then prove by induction on the positive integer n that

6.3Recalling from the previous exercise section the formulas for the volume α_n of the unit n-dimensional ball , deduce from the previous two exercises that

for all .

6.4Apply Exercises 6.1 and 6.2, and formulas (7) and (10), to obtain a new derivation of

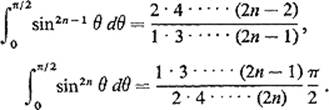
6.5Show that by subtituting x = t^1/2.

6.6Use the substitution t = xⁿ to show that

6.7 Use the substitution x = e^−u to show that

6.8Show that

6.9Prove that the integral defining the beta function converges.

6.10Show that the mass of a spherical ball of radius a, with density function d(x, y, z) = x²y²z², is M = 4πa⁹/945. Hint: Calculate the mass of the first octant. Introduce spherical coordinates, and use formulas (7) and (10).

6.11Use ellipsoidal coordinates to show that the mass of the ellipsoidal ball , with density function d(x, y, z) = x² + y² + z², is

6.12By integration by parts show that

Deduce from this recursion formula that

and

Apply Exercises 6.1 and 6.2 to conclude that

for all integers .

6.13The purpose of this exercise is to give a final computation of the volume α_n of the unit ball .

(a)Let T : ⁿ → ⁿ be the n-dimensional spherical coordinates mapping of Exercise 5.19. Note by inspection of the definition of T, without computing it explicitly, that the Jacobian of T is of the form

for some function γ.

(b)Let f: ⁿ → be an absolutely integrable function such that g = f T is a function of ρ alone. Then show that

for some constant C_n (independent of f). Setting f = g = 1 on Bⁿ, a = 1, we see that α_n = C_n/n, so it suffices to compute C_n.

(c)Taking limits in (*) as a → ∞, we obtain

so it suffices to find an absolutely integrable function f for which we can evaluate both of these improper integrals. For this purpose take

so . Conclude from Example 8 that , and then apply the previous exercise to compute C_n, and thereby α_n.

6.14The purpose of the problem is to evaluate

(a)First show that if x > 0.

(b)Then use integration by parts to show that

(c)Hence

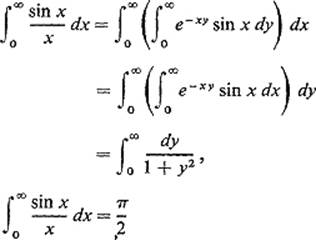
provided that the interchange of limit operations can be justified.

6.15The object of this problem is to show that f(x) = (sin x)/x is not absolutely integrable on (0, ∞). Show first that

Given any compact contented set , pick m such that , and then define

for all n > m. Now conclude, from the fact that diverges, that

Why does this imply that ∫_{(0, ∞)} [(sin x)/x] dx does not exist?

6.16If U is an open subset of ⁿ, show that there exists an increasing sequence of compact contented sets such that . Hint: Each point of U is contained in some closed ball which lies in U. Pick the sequence in such a way that A_k is the union of k closed balls.

6.17Let q(x) = x^tAx be a positive definite quadratic form on ⁿ. Then show that

Outline:Let P be the orthogonal matrix provided by Exercise II.8.7, such that P^tAP = P⁻¹AP is the diagonal matrix whose diagonal elements are the (positive) eigenvalues λ₁, . . . , λ_n of the symmetric matrix A. Use the linear mapping L : _yⁿ → _xⁿ defined by x = Py to transform the above integral to

Then apply the fact that by Example 8, and that fact that λ₁λ₂ · · · λ_n = det A by Lemma II.8.7.