High School Algebra I Unlocked (2016)

Lesson 6.4. Systems of Linear and Quadratic Equations

As you may remember from Chapter 5, a system of equations is a set of equations that share variables and work together in a coordinate plane. You may also remember that the solution to a system of equations is the point of intersection. Now we will expand upon this idea, introducing systems that have both linear and quadratic equations. You will solve such systems in the same way that you would a system of linear equations: by identifying the point(s) of intersection.

Need to review the
process for handling
systems of equations?
Flip back to Lesson
5.1 to refresh your
memory about the four
methods for solving a
system of equations!

A system of linear and quadratic equations can have no solution, one solution, or two solutions, depending on the number of intersections. When there is only one solution, such as that shown in the following system, the two equations hit at only one place, known as a tangent. Look at the following graphs.

Now it’s time for a couple of examples.

EXAMPLE

y = x² + 4x + 4

y = 2x − 1

Solve the system of equations graphically.

When you’re asked to solve the system of equations graphically, you need to graph both equations in the coordinate plane. You can factor the first equation, y = x² + 4x + 4, to find the roots as follows:

y = x² + 4x + 4

y = (x + 2)(x + 2)

The quadratic equation y = x² + 4x + 4 has a double root, or a single root at x = −2. The point (−2, 0) is also the vertex of the quadratic equation, and the axis of symmetry occurs at x = −2. Next, find the y-intercept of the quadratic by setting x = 0; thus, the y-intercept occurs at (0, 4). Using all this information, you can graph the quadratic y = x² + 4x + 4 as shown:

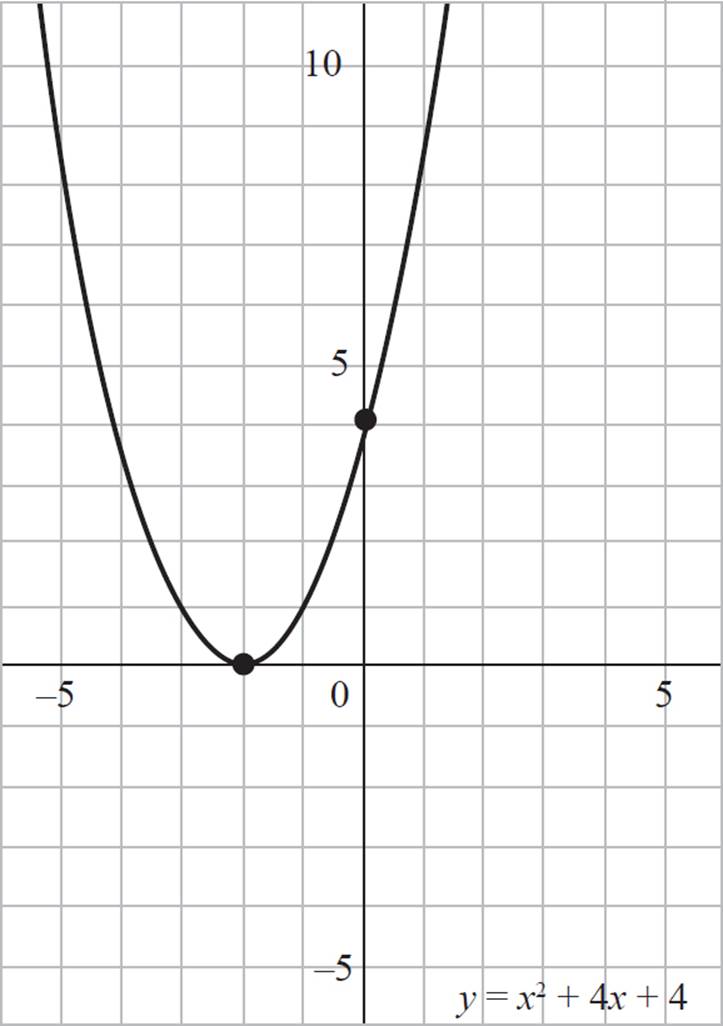
Next, graph the linear equation y = 2x − 1 by finding the x- and y-intercepts. To find the x-intercept, set y = 0 and solve for x: 0 = 2x − 1, 2x = 1, and x = 1/2. Accordingly, the x-intercept of the equation y = 2x − 1 occurs at (1/2, 0). To find the y-intercept, set x = 0 and solve for y: y = 2(0) − 1 and y = −1. Accordingly, the y-intercept of the equation y = 2x − 1 occurs at (0, −1). Thus, the linear equation y = 2x − 1 passes through the points (1/2, 0) and (0, −1) and can be drawn on our coordinate plane like this:

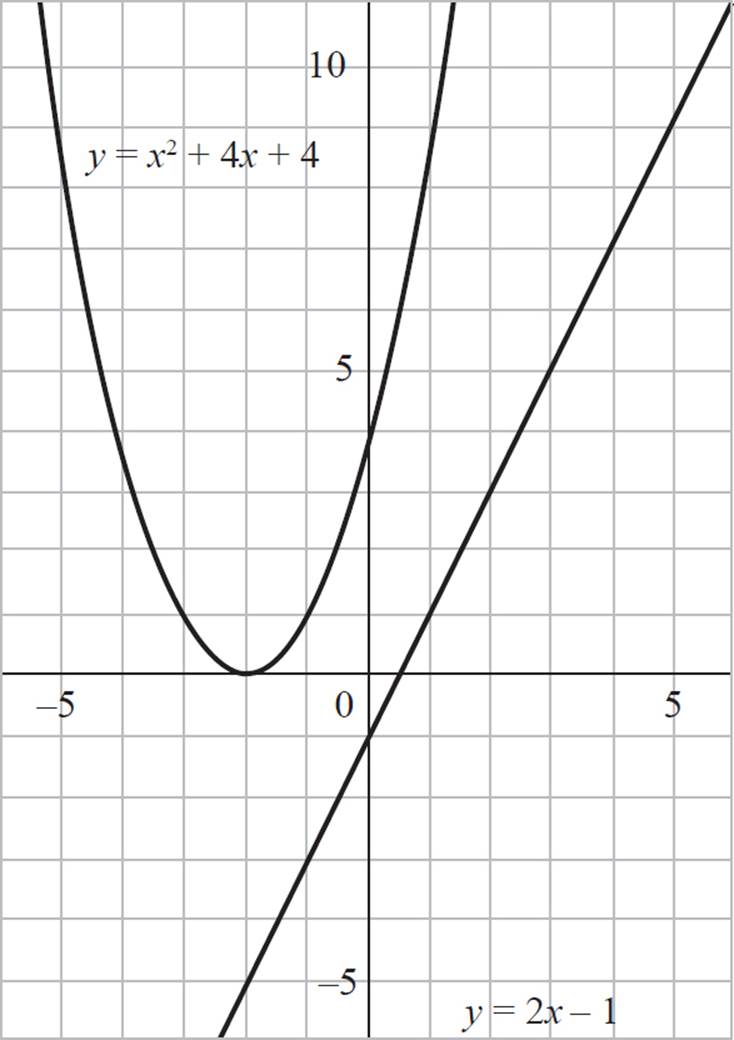
Once both equations have been graphed, you should be able to determine the solution to the system of equations. In this scenario, the two equations do not intersect, so there is no solution.

You can also solve a linear quadratic system of equations algebraically by setting the two equations equal to each other and determining the points of intersection. Try the next question.

EXAMPLE

y = −x² − x + 6

y = 3x + 6

Solve the system of equations algebraically.

In order to use the algebraic method, you must isolate either the x- or y-value in both equations. Since both of the equations represent the value of y, set the two equations equal to one another and simplify as follows:

3x + 6 = −x² − x + 6

x² + 3x + x + 6 − 6 = 0    

x² + 4x = 0   

Next, factor the quadratic and use the zero product property to find the x-values:

x² + 4x = 0

x(x + 4) = 0

Thus, x = 0 or x = −4. Now plug x = 0 or x = −4 into either of the original equations to solve for the corresponding y-values:

Therefore, the solutions to this system of equations are (−4, −6) and (0, 6).

If we were to graph the system of equations, we would find identical answers, as shown in the following graph of y = −x² − x + 6 and y = 3x + 6.

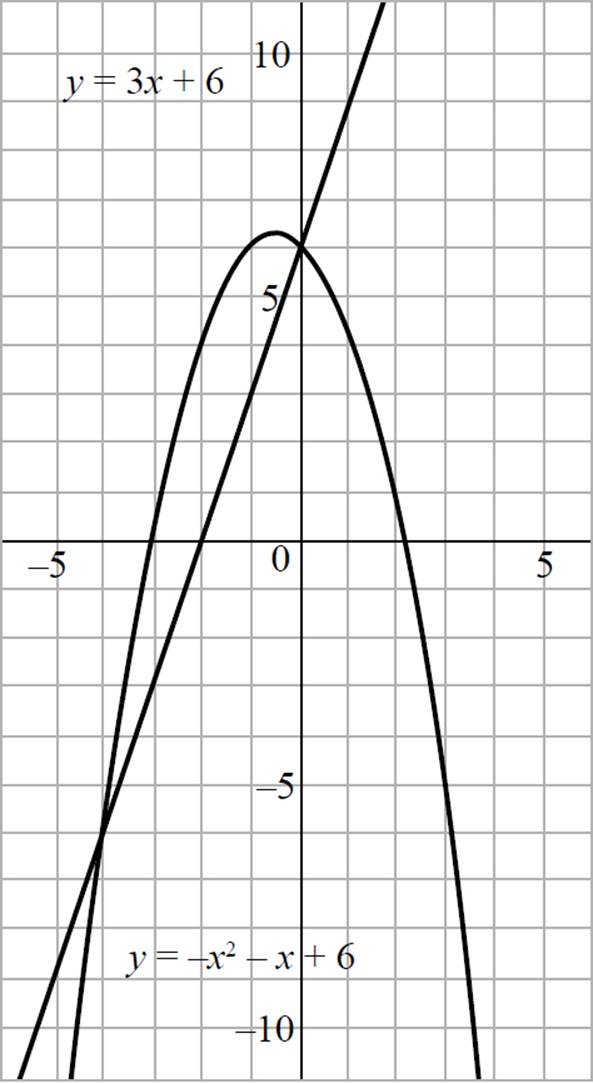
The bottom line is, regardless of the method you use to solve a system of linear and quadratic equations, the solutions will be identical.

Guess what? You’ve made it through this tricky chapter on quadratic equations and inequalities! Make sure you have a solid grasp of this information before moving on to the section on functions, which is up next. It’s essential to understand equations before tackling functions. Now solve the Practice Questions on your own, and complete the Reflect activity at the end of the chapter to assess your comfort level with the material.

DRILL

CHAPTER 6 PRACTICE QUESTIONS

Click here to download a PDF of Chapter 1 Practice Questions.

Directions: Complete the following problems as specified by each question. For extra practice, try using an alternative method to solve the problem or check your work.

1. Factor the quadratic y = x² + 45x − 196, and then identify the roots and the y-intercept of the equation.

2. Use the discriminant to determine the number of real solutions in the quadratic equation x² = 3x + 4, and then find the real solution(s).

3. In the equation 2x² − zx − 24 = x² − 2zx − 8, z is a nonnegative integer. What is the sum of the smallest and largest possible values of z ?

4. Find the vertex, axis of symmetry, and roots of 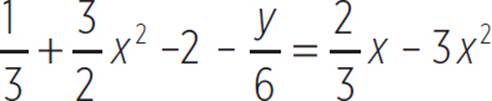by completing the square. Graph the result.

5. Use the quadratic formula to identify the vertex, the axis of symmetry, and the zeros of 12x² + 1 = 14x + 1 + y.

6. Graph the inequality + 2x² ≥ −x² + x + 4.

7. y = x² − 2x + 4

y = −8x − 5

Solve the system of equations algebraically and state whether the system has two solutions, one solution, or no solution.

8. −8x² +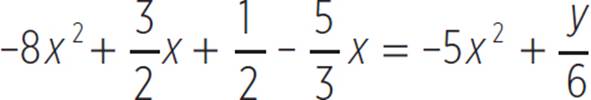

y = x + 4

Solve the system of equations graphically and state whether the system has two solutions, one solution, or no solution.

SOLUTIONS TO CHAPTER 6 PRACTICE QUESTIONS

1. Roots: (−49, 0) and (4, 0); y-intercept: (0, −196)

This question requires you to solve the quadratic y = x² + 45x − 196 by factoring, and graph the equation in the coordinate plane. The quadratic is already in standard form, ax² + bx + c = 0, which will be factored as (x + m)(x + n), where m and n are factors of c,and m + n = b. For the equation y = x² + 45x − 196, a = 1, b = 45, and c = −196. Based on the rules of factoring, if the value of c is negative and the value of b is positive, m and n will have different signs; thus you can set up your initial terms as follows: x² + 45x− 196 = (x + )(x − ). Next, find factors of the c-term, 196, that add up to the b-term, 45, noting that since the value of b is positive, the larger factor will be positive:

In the chart, the only factors of our c-term, 196, that add up to the b-term, 45, are −4 and 49. You can then fill in the rest of the parentheses as follows: x² + 45x − 196 = (x + 49)(x − 4).

Now that you’ve factored the quadratic, find the values of x by setting each parenthetical term to zero and solving for x:

Therefore, the roots of the quadratic equation x² + 45x − 196 = 0 occur when x = −49 or x = 4. Thus, the roots of the equation are (−49, 0) and (4, 0). Next, determine the y-intercept of the quadratic equation, y = x² + 45x − 196, by setting x = 0 and solving for y:y = x² + 45x − 196, y = (0)² + 45(0) − 196, and y = −196. Thus, the y-intercept is (0, −196).

2. x = 3 ±

Here you’re given the quadratic x² = 3x + 4 and asked to determine the number of solutions using the discriminant, b² − 4ac. The standard form of a quadratic expression is ax² + bx + c, so rewrite the equation in standard form to find that x² = 3x + 4 is x² − 3x − 4 = 0, and a = 1/2, b = −3, and c = −4. Plug these values into the discriminant formula and simplify: b² − 4ac = (−3)² − 4()(−4) = 9 − 4(−2) = 9 + 8 = 17. Since the discriminant is positive, the quadratic has two real solutions.

Now use the quadratic formula to find the solutions to the equation:

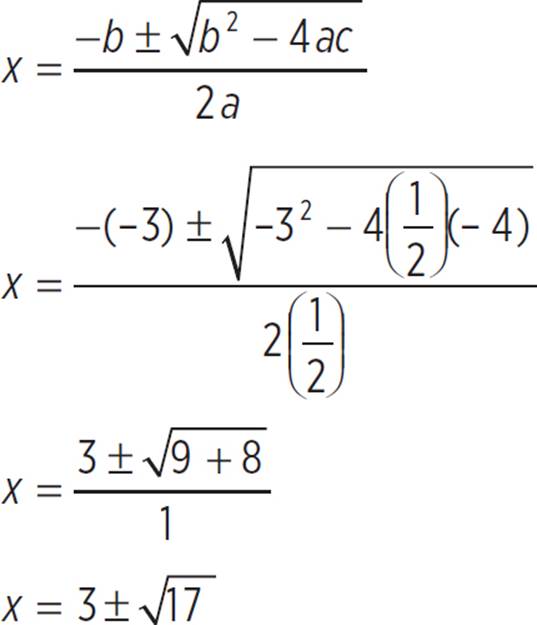
Therefore, the equation has two real solutions at x = 3 − and x = 3 + .

3. 15

You’re asked to find the sum of the largest and smallest possible values of z, given that z is nonnegative in the equation 2x² − zx − 24 = x² − 2zx − 8. Start by simplifying the equation and putting it in standard form: 2x² − zx − 24 = x² − 2zx − 8, 2x² − x² − zx + 2zx − 24 + 8 = 0, and x² + zx − 16 = 0. Then proceed as if you were factoring the quadratic, finding the factors of the c-term, −16, to find the possible values for b. Note that since b is positive and c is negative, the larger factor will be positive:

Based on the factor chart, the value of z could be 0, 6, or 15. Since the question asks you to find the sum of the smallest and largest possible nonnegative values of z, the answer is 0 + 15 = 15.

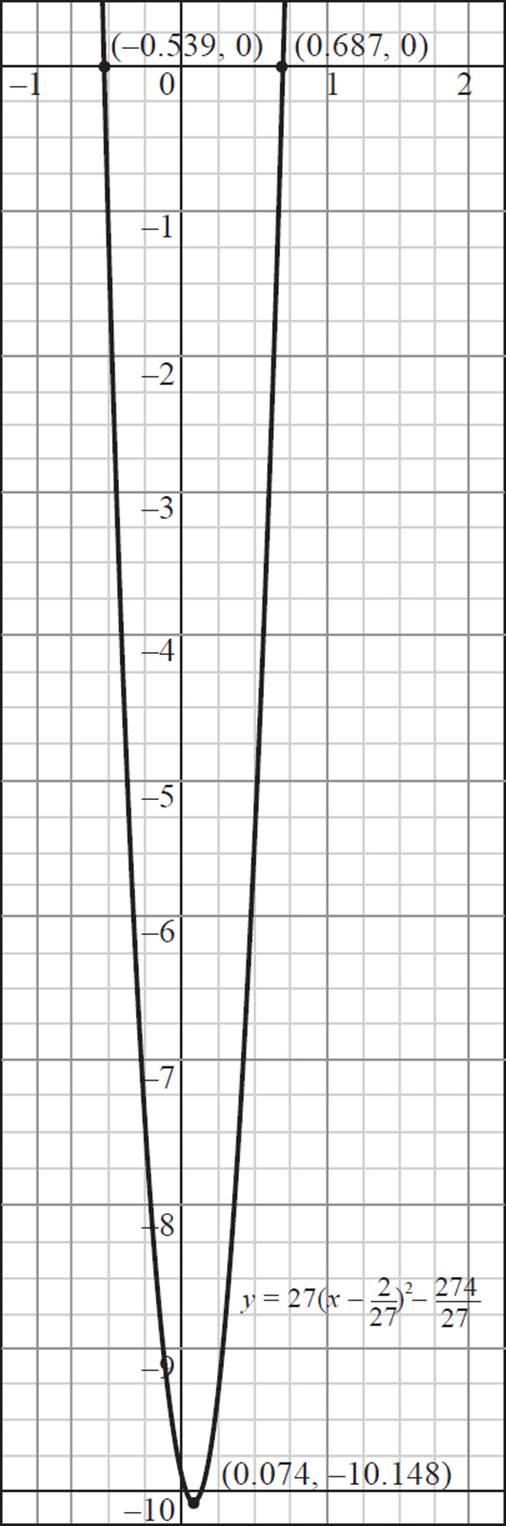
4. Roots: (−0.539, 0) and (0.687, 0); Vertex: 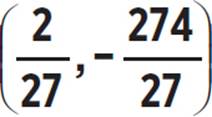or (0.074, −10.148); Axis of symmetry: x = or x = 0.074

This question requires you to find the vertex, axis of symmetry, and roots of + x² − 2 − = x − 3x² by completing the square. In order to complete the square, you must first simplify and rewrite the equation in the standard form of a quadratic equation, wherey = ax² + bx + c:

+ x² − 2 − = x − 3x²

+ x² − 2 − x + 3x² =     

1 + x² − 6 − 2x + 9x² =     

2 + 9x² − 12 − 4x + 18x² = y    

27x² − 4x − 10 = y  

Once the equation is in standard form, you know that a = 27, b = −4, and c = −10. Next, find the values of d and e to complete the square and factor the quadratic in the form a(x + d)² + e, where d = 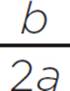and e = c − 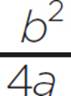. Using the values of a, b, and c and the formulas for d and e, you can find the value of d:

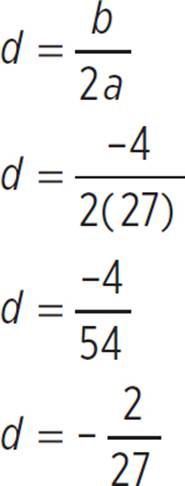
Now find the value of e, substituting the values of a, b, and c:

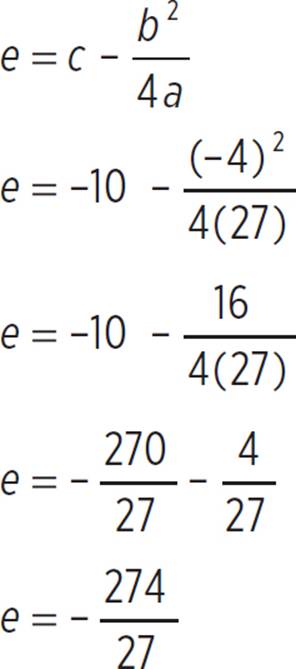
Substitute in the values a = 3, d = − , e = −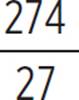 into the quadratic form associated with completing the square: a(x + d)² + e and 27(x − )² − 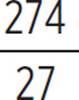= 0. Now that you’ve completed the square, set the factored expression equal to zero, simplify the equation, and solve for x:

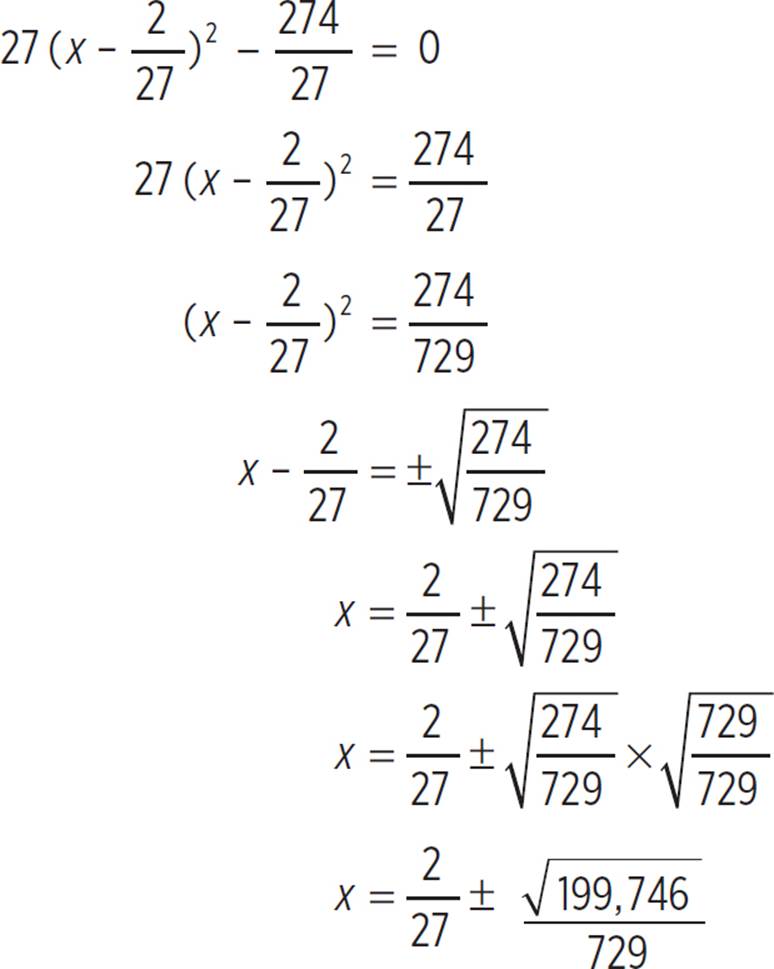
Although you can keep the answer in fraction form, it might be easier to convert the fractions to decimals for the purpose of graphing; in which case, you’ll find that x = 0.074 + 0.613 or x = 0.074 − 0.613, and x = −0.539 or x = 0.687. Thus, the roots of the quadratic equation y = 27x² − 4x − 10 occur at (−0.539, 0) and (0.687, 0).

Now you need to identify the axis of symmetry and the vertex of the quadratic. Here, the quadratic written as 27(x − )² − 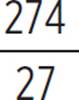= 0 is similar to the vertex form of a quadratic, y = a(x − h)² + k, where (h, k) is the vertex. Thus, for the quadratic 27(x − )² − 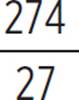= 0, h = or 0.074, k = −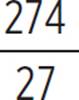 or −10.148, and a vertex of (, −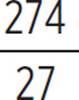) or (0.074, −10.148). Finally, you can find the axis of symmetry. Since the vertex is (0.074, −10.148), the axis of symmetry of the quadratic 27(x − )² − 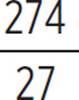= 0 is x = or x = 0.074.

Therefore, the quadratic equation y = 27x² − 4x − 10 has a vertex of (0.074, −10.148), an axis of symmetry of x = 0.074, and roots (−0.539, 0) and (0.687, 0). You can then use this information to graph the quadratic.

5. Roots: (0, 0) and 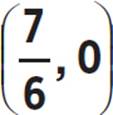; Vertex: 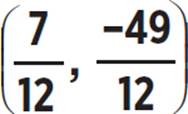or (0.58, −4.08); Axis of symmetry: x = or x = 0.58

You need to use the quadratic formula to find the vertex, the axis of symmetry, and the zeros of the quadratic equation 12x² + 1 = 14x + 1 + y. Start by simplifying the quadratic and putting it into standard form, y = ax² + bx + c: 12x² + 1 = 14x + 1 + y, and y = 12x² − 14x = 0.

Now we know that a = 12, b = −14, and, because there is no c-term, c = 0. Plug these values into the quadratic equation and simplify as follows:

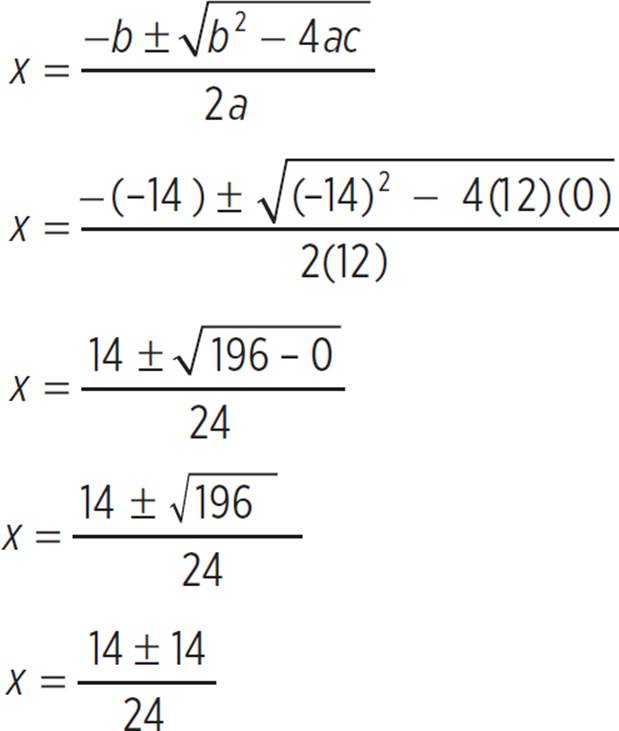
x = or x = , and x = 0 or x =

Thus, roots of the quadratic equation 12x² −14x = 0 are at (0, 0) and 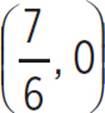. Next, you need to find the vertex (h, k) of the quadratic equation, which is equal to 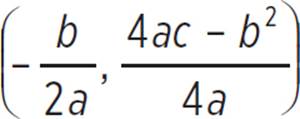. In our quadratic equation 12x² −14x = 0, we know that a = 12, b = −14, and c = 0. Therefore, the vertex (h, k) of the quadratic equation is 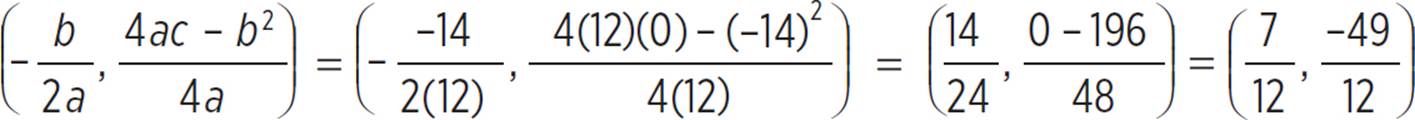or (0.583, −4.083).

Finally, you can determine that the axis of symmetry, which is equal to x = −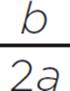, of the quadratic equation 12x² −14x = 0. Since the axis of symmetry is equal to the h-coordinate of vertex (h, k), which you already solved, you know that the axis of symmetry is x = or or 0.583. Therefore, the vertex of the quadratic equation 12x² −14x = 0 is 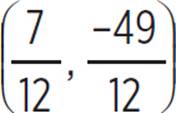or (0.583, −4.083), the axis of symmetry is x = or 0.583, and the roots occur at (0, 0) and .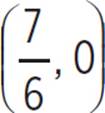

6. Roots: (, 0) and (−1, 0); Vertex: (, ) or (0.1, 8.1)

You’re given the inequality + 2x² ≥ −x² + x + 4 and asked to graph the solution. Follow the process for solving linear inequalities, starting by replacing the inequality sign with an equals sign and solving for x:

+ 2x² = −x² + x + 4 

y + 4x² = −2x² + 2x + 8

   y = −4x² − 2x² + 2x + 8

 y = −6x² + 2x + 8

Since the equation is now in standard form, ax² + bx + c = 0, you know that a = −6, b = 2, and c = 8. Plug these values into the quadratic equation and simplify:

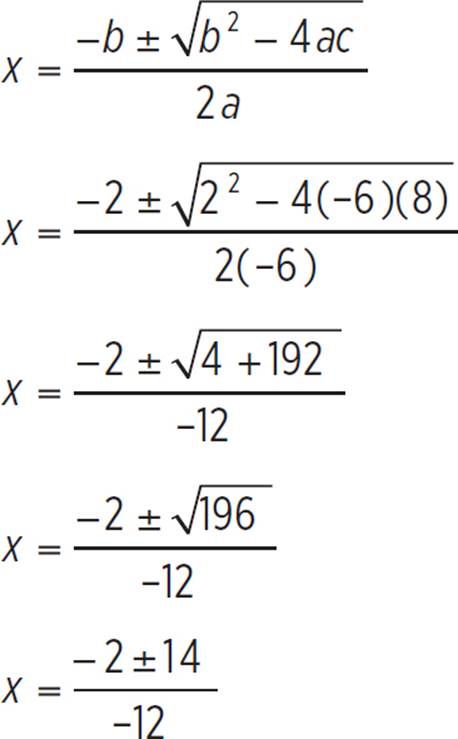
x = 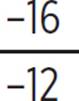and x = 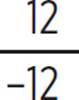, and x = and x = −1

Now that you’ve found that the roots of the parabola are x = 4/3 and x = −1, find the vertex with the formula (h, k) = 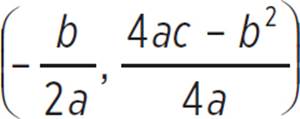. Therefore, the vertex (h, k) of the inequality y ≥ −6x² + 2x + 8, where a = −6, b = 2, and c = 8:

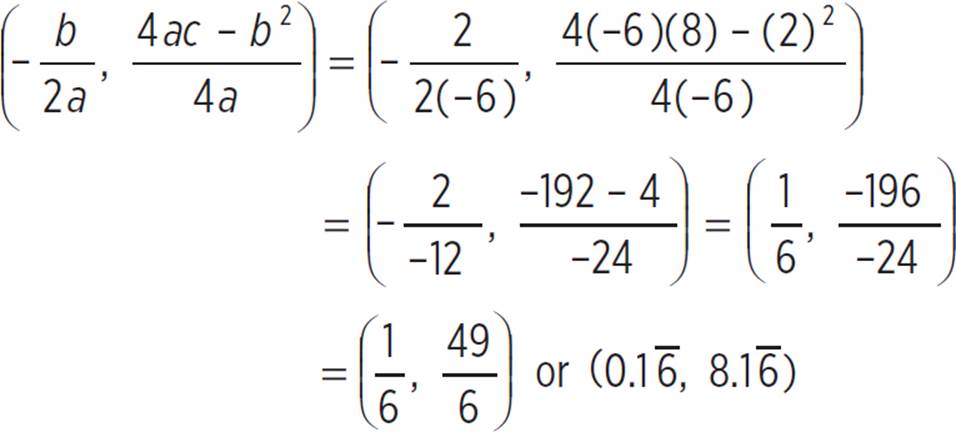
Next, plot the roots and vertex on the coordinate plane and graph the inequality, using a solid line since the inequality contains a greater than or equal to sign.

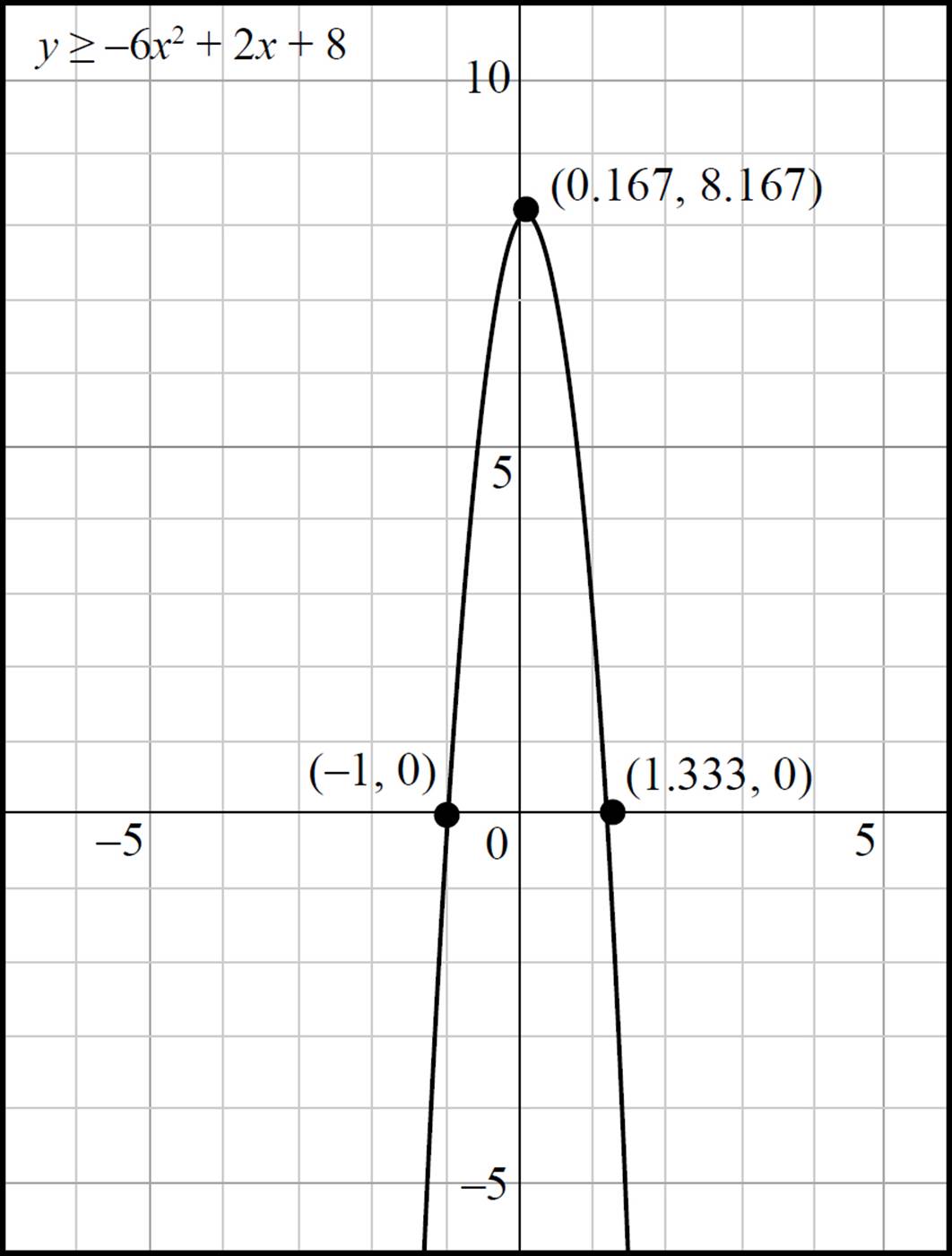
Finally, you must determine which side of the parabola to shade by selecting a test point that falls either inside or outside of the parabola and determining if the original inequality holds true. Since the origin does not fall on the parabola, test the point (0, 0) in the original inequality, y ≥ −6x² + 2x + 8: y ≥ −6x² + 2x + 8, 0 ≥ −6(0)² + 2(0) + 8, 0 ≥ 0 + 0 + 8, and 0 ≥ 8. Since 0 is not greater than 8, the statement is false, and the area outside the parabola should be shaded.

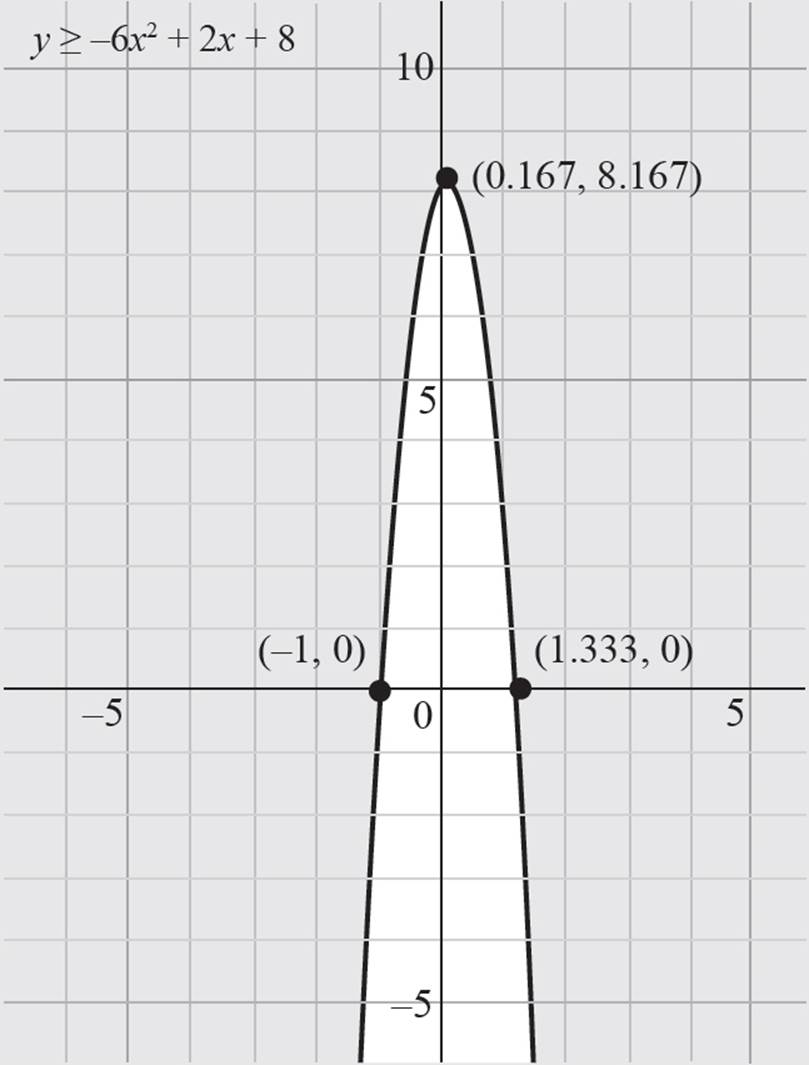
7. One solution, (−3, 19)

This question requires you to solve a linear-quadratic system of equations algebraically, given that y = x² − 2x + 4 and y = −8x − 5. To solve a linear-quadratic system algebraically, isolate either the x- or y-value in both equations. Here, y is already isolated in both equations, so you can set the two equations equal to one another and simplify as follows:

x² − 2x + 4 = −8x − 5

x² − 2x + 4 + 8x + 5 = 0

x² + 6x + 9 = 0

With the equation in standard form, ax² + bx + c = 0, you know that a = 1, b = 6, and c = 9. Now you need to find factors of the c-term, 9, that add up to the b-term, 6, noting that since b and c are both positive, both factors will be positive:

Since the only factors of 9 (c-term) that add up to 6 (b-term) are 3 and 3, you can factor the quadratic equation x² + 6x + 9 = 0 as (x + 3)(x + 3). Now find the values of x by setting each parenthetical term to zero and solving for x, noting that since each term is identical, you have a double root.

Therefore, the root of the quadratic equation x² + 6x + 9 = 0 is x = −3.

Now that you’ve found x = −3, plug this value into either of the original equations to solve for the corresponding y-value. If you plug x = −3 into the equation y = −8x − 5, you will find that y = −8(−3) − 5, y = 24 − 5, and y = 19. Therefore, the solutions to this system of equations is (−3, 19).

8. No solution

This question requires you to solve a linear-quadratic system of equations graphically, given that −8x² + x + − x = −5x² + and y = x + 4. In order to graph the quadratic equation, you first need to put the equation into the standard form of a quadratic, ax²+ bx + c:

−8x² + x + − x = −5x² +

−48x² + 9x + 3 − 10x = −30x² + y

    y = 30x² − 48x² − x + 3

    y = −18x² − x + 3

Unfortunately, this equation is not easily factored, so find the x-intercepts of the equation using the quadratic formula, where a = −18, b = −1, and c = 3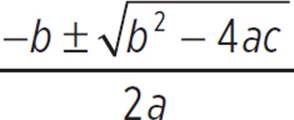: x = 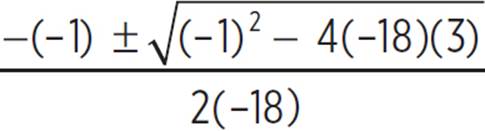, x = , x = 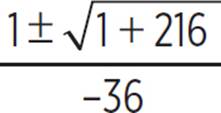, and x 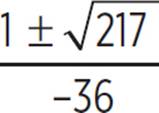or x = 0.381 or x = −0.437. Therefore, the roots of the quadratic occur at (0.381, 0) and (−0.437, 0).

Now find the vertex of the quadratic with the formula (h, k) = 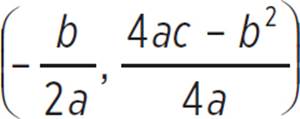, where a = −18, b = −1, and c = 3:

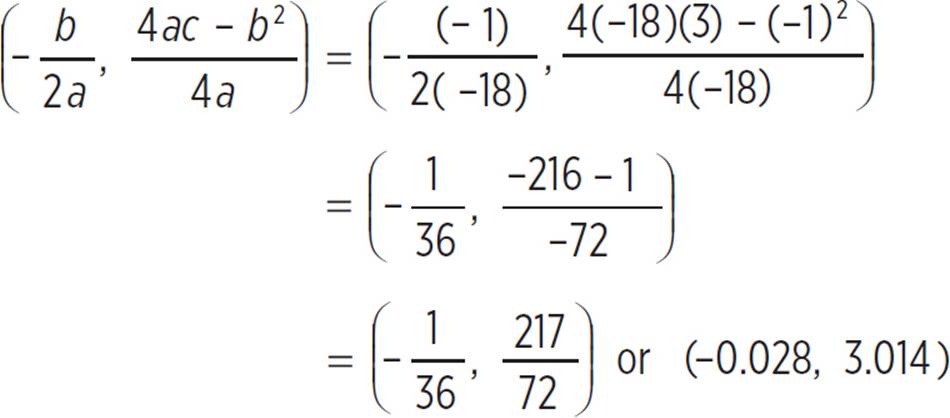
Next, find the y-intercept of the quadratic by setting x = 0; thus, the y-intercept occurs at (0, 3). Using this information, you can graph the quadratic y = −18x² − x + 3 as shown:

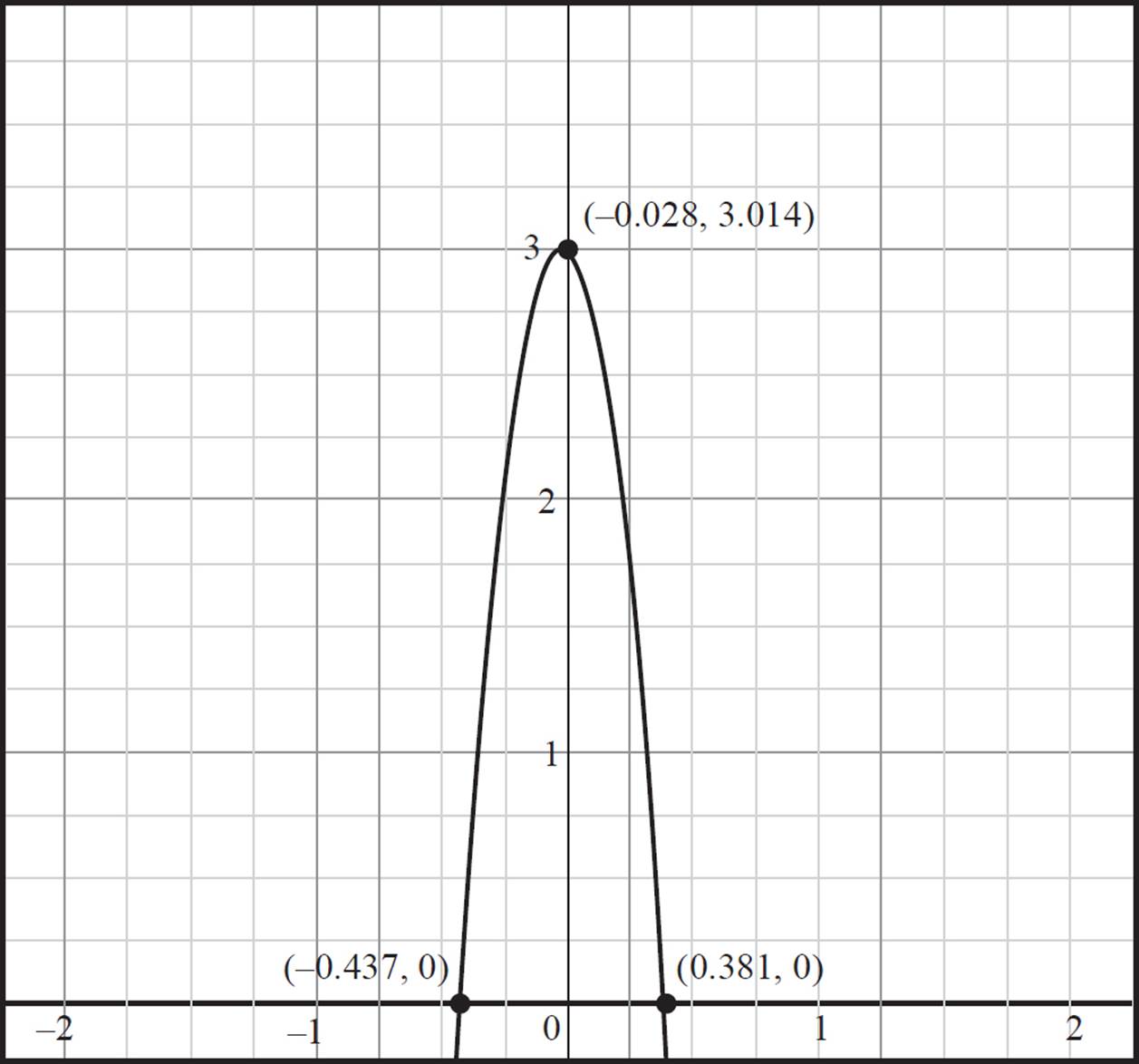
Next, you can graph the linear equation y = x + 4 by finding the x- and y-intercepts. To find the x-intercept, set y = 0 and solve for x:

y = x + 4

0 = x + 4

x = −4 

x = −8 

Thus, the x-intercept is (−8, 0). To find the y-intercept, set x = 0 and solve for y:

y = x + 4

y = (0) + 4

y = 4  

Thus, the y-intercept is (0, 4). The linear equation y = x + 4 passes through the points (−8, 0) and (0, 4), and can be drawn on the coordinate plane:

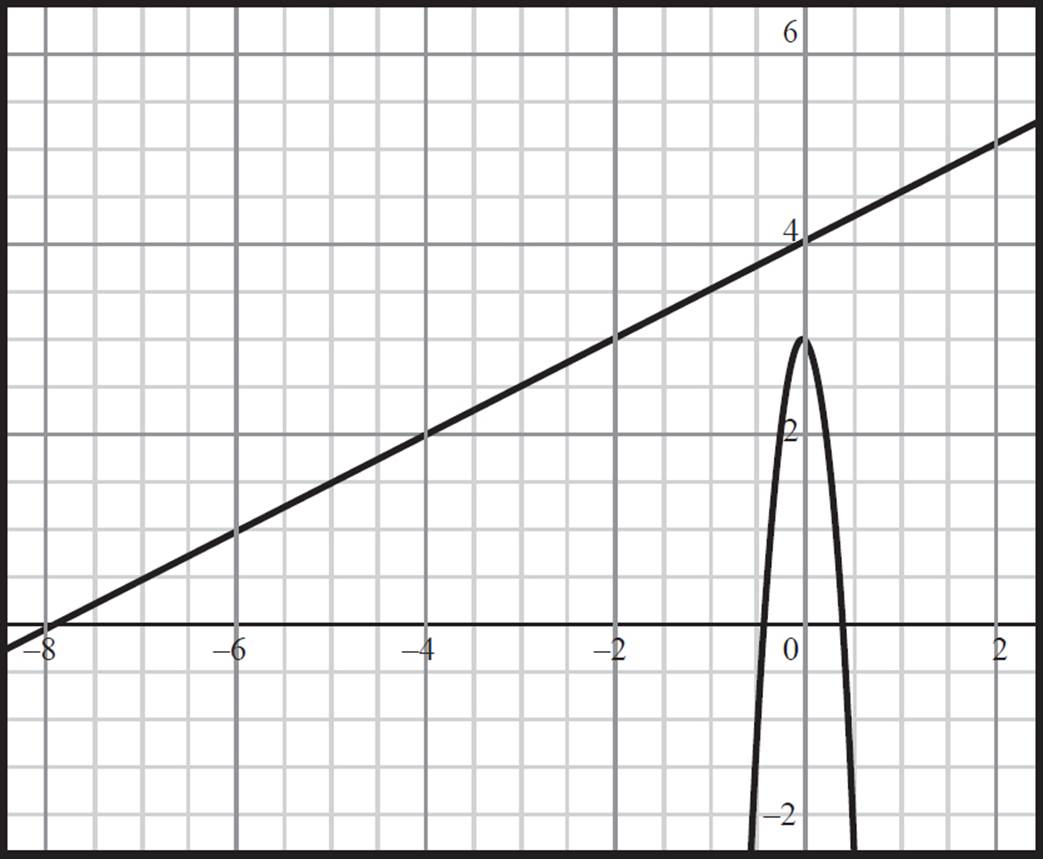
Since the linear equation and the quadratic equation do not intersect, there is no solution to this system of equations.

REFLECT

Congratulations on completing Chapter 6!

Here’s what we just covered.

Rate your confidence in your ability to:

•Explain how quadratic equations can model real-life situations

1 2 3 4 5

•Identify the graphs of quadratic, cubic, quartic, and quintic equations

1 2 3 4 5

•Solve quadratic equations and quadratic inequalities using methods such as factoring, completing the square, and the quadratic formula

1 2 3 4 5

•Graph quadratic equations and inequalities

1 2 3 4 5

•Determine the vertex and axis of symmetry of quadratic equations and inequalities

1 2 3 4 5

•Determine the number of solutions of a quadratic using the discriminant

1 2 3 4 5

•Solve linear-quadratic systems of equations

1 2 3 4 5

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.

CHAPTER 6 KEY POINTS

The standard form of a quadratic equation is ax² + bx + c = 0, where x is the variable and a, b, and c, are constants, and a ≠ 0.

A quadratic equation is an equation of degree 2, which means it has at least one squared term, and no term has an exponent greater than 2.

The curve created by a quadratic equation is known as a parabola.

The solutions of a quadratic equation, also referred to as the roots or zeros of a quadratic, are the points where the equation is equal to zero.

The zero product property states that if a × b = 0, then a = 0, b = 0, or both a = 0 and b = 0.

The vertex form of a quadratic is given by y = a(x − h)² + k, where (h, k) is the vertex.

○ If the value of a is positive, the graphed quadratic will resemble a smile.

○ If the value of a is negative, the quadratic will resemble a frown.

The quadratic formula is x = .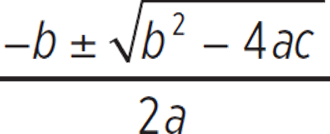

The vertex (h, k) for any quadratic ax² + bx + c can be determined with (h, k) = .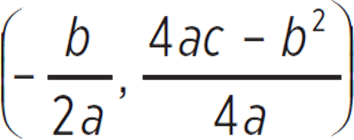

The axis of symmetry for any quadratic ax² + bx + c can be determined with x = −.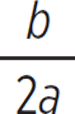

The discriminant is b² − 4ac.

○ If the discriminant is positive, the quadratic equation will have two real solutions.

○ If the discriminant is zero, the quadratic equation will have one real solution.

○ If the discriminant is negative, the quadratic equation will have two complex solutions, or solutions that include the imaginary number i.

A system of linear and quadratic equations can have no solution, one solution, or two solutions, depending on the number of intersections.

○ When there is only one solution, the two equations intersect at only one place, known as a tangent.