Master AP Calculus AB & BC

Part II. AP CALCULUS AB & BC REVIEW

CHAPTER 3. Limits and Continuity

EVALUATING LIMITS ANALYTICALLY

At this point in your mathematics career, you possess certain polished skills. For example, if asked “Flow many is 4 + 5?” you would not need nine apples in order to reach a solution. In the same way, you can evaluate most limits without actually looking at a graph of the given function. In fact, you don’t need fruit of any kind to evaluate limits analytically. Instead, you need to learn the three major methods of finding limits: substitution, factoring, and the conjugate methods.

Remember that limits answer the question “Where is a function heading?” Luckily for math nerds all over the world (like me), a function usually reaches the destination for which it was heading. In such cases, you can use the substitution method for evaluating limits. It should be the first method you try in every limit problem you encounter.

Example 1: Evaluate the following limits:

Substitute x = 2 into the function to get 2² — 4 ∙ 2 + 9 = 5. Thus, That’s all there is to it.

Substitution is again the way to go:

NOTE. The only appreciable difference between and x - 4 is that is undefined when x = -1. Though technically unequal, the functions share identical limit values everywhere.

If all limits were possible via direct substitution, however, you would have done limits in basic algebra, and everyone would, in general, be happier. Sometimes, substitution will not work, because the result is illegal. For example, consider the function with which you experimented in Hands-On Activity 3.1: If you try direct substitution, the result is The technical term for a result of 0/0 is indeterminate, which means that you cannot determine the limit using this method. (And you were just starting to feel confident...) Luckily, just in the knick of time, in rides the factoring method of evaluating limits on a shiny white steed.

Example 2: Evaluate

Solution: The factoring method entails factoring the expression and then simplifying it. This numerator factors easily, giving you Next, cancel the common factors in the fraction to get Therefore, Although substitution did not work before, it certainly will in the new expression, so the same result you reached in Activity 3.1. Huzzah! The last limit evaluation method has a very specific niche in life—it attacks radical expressions in limits. This makes deciding to apply the conjugate method relatively easy. This technique is based on a simple complex number concept you have most likely already learned (although you won’t be using it to simplify complex numbers in this application).

Example 3: Evaluate

Solution: Substitution will result in the indeterminate answer 0/0, and factoring isn’t as fruitful as it was in Example 2. To evaluate this limit, multiply the fraction by the conjugate of the radical expression divided by itself:

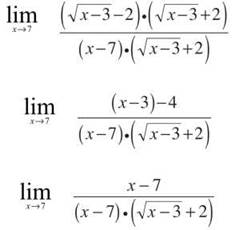
NOTE. The conjugate of the complex number a - bi is the complex number a + bi. To take the conjugate, change the sign that combines the terms to its opposite.

It’s best to leave the denominator alone initially, as you can now cancel the common (x — 7) term to get

Now, substitution is possible, and the answer is

EXERCISE 2

Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.

DO NOT USE A CALCULATOR FOR PROBLEMS 1 THROUGH 6.

Evaluate the following limits, if they exist.

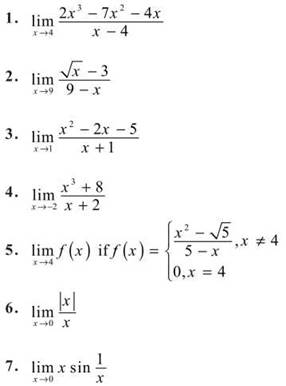
ANSWERS AND EXPLANATIONS

TIP. While undertaking the factoring or conjugate methods, make sure to leave the in front of each successive line—the limits of each step are equal, but the functions themselves are not always equal.

1. Direct substitution results in the indeterminate form 0/0 and cannot be used. The best option is factoring—doing so results in Eliminating the common factor gives you Substitution is now allowed, and the answer is 36.

2. Substitution (always your first method to attempt) fails. The presence of a radical alerts you to use the conjugate method:

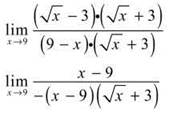
Notice that you have to factor a — 1 out of (9 — x) in the denominator to be able to match the (x — 9) in the numerator.

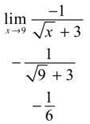
3. Although you may want to apply factoring in this example because of the presence of polynomials, substitution works—don’t forget to try substitution first:

4. Because substitution fails and there are no radicals, factoring is the method to use. In fact, the numerator is a sum of perfect cubes and factors easily.

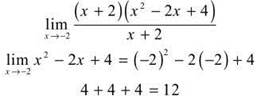
5. Don’t be distracted by the fact that f(4) = 0. This does not mean that If you graph the function, you’ll see that f(x) is not heading for a height (limit) of zero when x = 4. The graph is headed for the height defined by the rule that is true for all x ≠ 4. Substitution works for this function. So, the limit is

6. None of your methods will apply in this problem, so you’ll need to draw a graph (use a table of values):

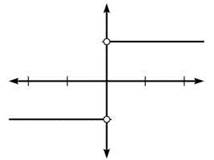
Once you do, you’ll see that the left-hand limit at x = 0 is —1 and the right-hand limit at x = 0 is 1; thus, there is no general limit, and does not exist.

7. You currently have no good methods to evaluate this limit, so look at the graph as v approaches 0 from the left and the right:

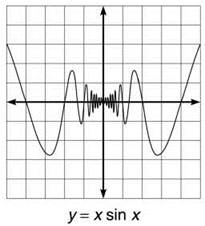
Visually, you can determine that the function approaches a limit (height) of zero as you near x = 0.