Master AP Calculus AB & BC
Part II. AP CALCULUS AB & BC REVIEW
CHAPTER 3. Limits and Continuity
HANDS-ON ACTIVITY 3.2: THE EXTREME VALUE THEOREM
NOTE. The intervals of continuity for trigonometric functions are the intervals that make up their domains, as trigonometric functions are continuous on their entire domains.
This and the next activity introduce you to two basic but important continuity theorems. Note that both of these are called existence theorems. They guarantee the existence of certain values but do not tell you where these values are—it’s up to you to find them, and they’re always in the last place you look (with your car keys, your wallet from two years ago, and the words to that Bon Jovi song you used to know by heart).
1. Given f(x) = x4 — 3x — 4, justify that f(x) is continuous on the x interval [—1,2].
_____________________________________________________
_____________________________________________________
2. Draw the graph of f(x). Use a graphing calculator if you wish.
3. The maximum height reached by f(x) on the interval [—1,2] is called the maximum of f on the interval. At what value of x does f(x) reach its maximum, and what is that maximum value?
_____________________________________________________
_____________________________________________________
4. To calculate the minimum value of f(x), use the 2nd→Trace→minimum function on your calculator. Set bounds to the left and the right of the minimum and make a guess, as you did when finding x-intercepts in Chapter 2. What is the minimum value of f(x) on [—1,2]?
_____________________________________________________
NOTE. You are not allowed to use the maximum/minimum functions of your calculator on the AP exam. We will learn how to find them in different ways (which are acceptable on the test) later.
5. At what x-value does the minimum occur? (Hint: The value is displayed when you calculate the minimum with the calculator.)
_____________________________________________________
6. Graph g(x) = 1/x on the axes below. Can you find a maximum and a minimum for g(x) on the x interval (1,5)?

7. Why do your results for f and g differ?
_____________________________________________________
8. Graph ![]() below. Why is there no maximum on [0,3]?
below. Why is there no maximum on [0,3]?

_____________________________________________________
_____________________________________________________
ALERT! If the EVT conditions are not satisfied, a function can still have a maximum, a minimum, or both—their existence is just not guaranteed in that case.
9. Complete the Extreme Value Theorem, based on your work above:
Extreme Value Theorem: Any function, f(x), will have a maximum and a minimum on the _________ interval _________ as long as f(x) is _________.
10. Visually speaking, where can maximums and minimums occur on a graph?
_____________________________________________________
SELECTED SOLUTIONS TO HANDS-ON ACTIVITY 3.2
1. f is a polynomial whose domain is (—∞,∞), and polynomials are continuous on their entire domain (remember the red parrot?)
3. f reaches its highest point on [—1,2] when x = 2, and f(2) = 6. Thus, f has a maximum of 6.
4. f has a minimum of —6.044261. If you can’t get this, use a left bound of 0, a right bound of 2, and a guess of 1.
5. The minimum occurs at x = .9085621.
6. You cannot find a maximum or a minimum. Although g(1) = 1 and g(5) = 1/5 would be the maximum and minimum values, respectively, they are not included on the open interval (1,5). You cannot choose an x value whose function value is higher or lower than every other in the interval—try it!
7. You used a closed interval with f and an open interval with g.
8. h is removably discontinuous at x = 0, and because the maximum would have occurred there, the function will have no maximum.
9. Any function, f(x), will have a maximum and minimum on the closed interval [a,b] as long as f(x) is continuous. If the interval is not closed or the function is discontinuous, the guarantees of the Extreme Value Theorem do not apply.
10. The maximum and minimum (together called extrema, since they represent the extreme highest and lowest points on the graph) will occur at “humps” on the graph (like the minimum of f) or at the endpoints of the interval (like f’s maximum).
EXERCISE 4
Directions: Solve each of the following problems. Decide which is the best of the choices given and indicate your responses in the book.
YOU MAY USE YOUR CALCULATOR FOR ALL OF THESE PROBLEMS
For each of the following functions and intervals, determine if the Extreme Value Theorem applies, and find the maximum and minimum of the function, if possible.
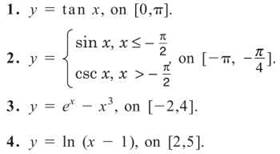
ANSWERS AND EXPLANATIONS
ALERT! In problem 2, a common mistake is to say that the maximum of the function is 2, but that is only the x-value at which the maximum occurs.
1. The Extreme Value Theorem (EVT) does not apply because tan x is discontinuous on the given interval, specifically at x = π/2. No maximum or minimum values are possible on the closed interval, as the function both increases and decreases without bound at x = π/2.
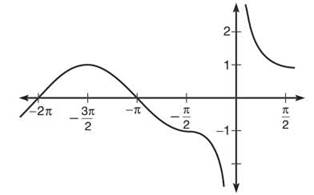
2. The function is continuous on the interval. Both parts of the function are trigonometric and, therefore, continuous on their domain, and [—π,—π/4] is included in the domain of each. The only possible discontinuity comes at x = —π/2, but both functions have the same value there, guaranteeing that the function is continuous. See the below graph—there is no break or jump. The EVT will apply. The maximum is 0 and occurs at x = —π, as the function decreases for the remainder of the interval. The minimum is 2/√2 = —1.414 and occurs at x = —π/4.
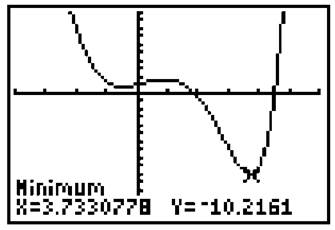
3. The EVT will not apply, but the function still has a maximum and minimum. The maximum occurs at the point (—2,8.135), and the minimum occurs at the point (3.733,—10.216). (The minimum is found using the minimum function on your graphing calculator.)
4. Although In (x — 1) is discontinuous at x = 1, ln (x — 1) is continuous on the given interval [2,5], so the EVT will apply. Because In x is monotonic and increasing, the minimum (0) will occur at the beginning of the interval, and the maximum (1.386) will occur at the end of the interval.