5 Steps to a 5: AP Calculus AB 2017 (2016)
STEP 3
Develop Strategies for Success
CHAPTER 4 How to Approach Each Question Type
CHAPTER 4
How to Approach Each Question Type
IN THIS CHAPTER
Summary: Knowing and applying question-answering strategies helps you succeed on tests. This chapter provides you with many test-taking tips to help you earn a 5 on the AP Calculus exam.
Key Ideas
![]() Read each question carefully.
Read each question carefully.
![]() Do not linger on a question. Time yourself accordingly.
Do not linger on a question. Time yourself accordingly.
![]() For multiple-choice questions, sometimes it is easier to work backward by trying each of the given choices. You will be able to eliminate some of the choices quickly.
For multiple-choice questions, sometimes it is easier to work backward by trying each of the given choices. You will be able to eliminate some of the choices quickly.
![]() For free-response questions, always show sufficient work so that your line of reasoning is clear.
For free-response questions, always show sufficient work so that your line of reasoning is clear.
![]() Write legibly.
Write legibly.
![]() Always use calculus notations instead of calculator syntax.
Always use calculus notations instead of calculator syntax.
![]() If the question involves decimals, round your final answer to 3 decimal places unless the question indicates otherwise.
If the question involves decimals, round your final answer to 3 decimal places unless the question indicates otherwise.
![]() Trust your instincts. Your first approach to solving a problem is usually the correct one.
Trust your instincts. Your first approach to solving a problem is usually the correct one.
![]() Get a good night’s sleep the night before.
Get a good night’s sleep the night before.
4.1 The Multiple-Choice Questions
• There are 45 multiple-choice questions for the AP Calculus AB exam. These questions are divided into Section I–Part A, which consists of 30 questions for which the use of a calculator is not permitted; and Section I–Part B with 15 questions, for which the use of a graphing calculator is allowed. The multiple-choice questions account for 50% of the grade for the whole test.
• Do the easy questions first because all multiple-choice questions are worth the same amount of credit. You have 60 minutes for the 30 questions in Section I–Part A and 45 minutes for the 15 questions in Section I–Part B. Do not linger on any one question. Time yourself accordingly.
• There is no partial credit for multiple-choice questions, and you do not need to show work to receive credit for the correct answer.

• Read the question carefully. If there is a graph or a chart, look at it carefully. For example, be sure to know if the given graph is that of f (x ) or f ′(x ). Pay attention to the scale of the x and y axes, and the unit of measurement.
• Never leave a question blank since there is no penalty for incorrect answers.

• If a question involves finding the derivative of a function, you must first find the derivative, and then see if you need to do additional work to get the final answer to the question. For example, if a question asks for an equation of the tangent line to a curve at a given point, you must first find the derivative, evaluate it at the given point (which gives you the slope of the line), and then proceed to find an equation of the tangent line. For some questions, finding the derivative of a given function (or sometimes, the antiderivative), is only the first step to solving the problem. It is not the final answer to the question. You might need to do more work to get the final answer.

• Sometimes, it is easier to work backward by trying each of the given choices as the final answer. Often, you will be able to eliminate some of the given choices quickly.
• If a question involves decimal numbers, do not round until the final answer, and at that point, the final answer is usually rounded to 3 decimal places. Look at the number of decimal places of the answers in the given choices.
• Trust your instincts. Usually your first approach to solving a problem is the correct one.
4.2 The Free-Response Questions
• There are 6 free-response questions in Section II: Part A consisting of 2 questions which allow the use of a calculator, and Part B with 4 questions which do not permit the use of a calculator. The 6 free-response questions account for 50% of the grade for the whole test.
• Read, Read, Read. Read the question carefully. Know what information is given, what quantity is being sought, and what additional information you need to find in order to answer the question.

• Always show a sufficient amount of work so that your line of reasoning is clear. This is particularly important in determining partial credit. In general, use complete sentences to explain your reasoning. Include all graphs, charts, relevant procedures, and theorems. Clearly indicate all the important steps that you have taken in solving the problem. A correct answer with insufficient work will receive minimal credit.
• When appropriate, represent the given information in calculus notations. For example, if it is given that the volume of a cone is decreasing at 2 cm3 per second, write 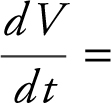 –2 cm3 /sec. Similarly, represent the quantity being sought in calculus notations. For example, if the question asks for the rate of change of the radius of the cone at 5 seconds, write “Find
–2 cm3 /sec. Similarly, represent the quantity being sought in calculus notations. For example, if the question asks for the rate of change of the radius of the cone at 5 seconds, write “Find 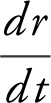 at t = 5 sec.”
at t = 5 sec.”

• Do not forget to answer the question. Free-response questions tend to involve many computations. It is easy to forget to indicate the final answer. As a habit, always state the final answer as the last step in your solution, and if appropriate, include the unit of measurement in your final answer. For example, if a question asks for the area of a region, you may want to conclude your solution by stating that “The area of the region is 20 square units.”
• Do the easy questions first. Each of the 6 free-response questions is worth the same amount of credit. There is no penalty for an incorrect solution.
• Pay attention to the scales of the x and y axes, the unit of measurement, and the labeling of given charts and graphs. For example, be sure to know whether a given graph is that of f (x ) or f ′(x ).
• When finding relative extrema or points of inflection, you must show the behavior of the function that leads to your conclusion. Simply showing a sign chart is not sufficient.

• Often a question has several parts. Sometimes, in order to answer a question in one part of the question, you might need the answer to an earlier part of the question. For example, to answer the question in part (b), you might need the answer in part (a). If you are not sure how to answer part (a), make an educated guess for the best possible answer and then use this answer to solve the problem in part (b). If your solution in part (b) uses the correct approach but your final answer is incorrect, you could still receive full or almost full credit for your work.
• As with solving multiple-choice questions, trust your instincts. Your first approach to solving a problem is usually the correct one.
4.3 Using a Graphing Calculator
• The use of a graphing calculator is permitted in Section I–Part B multiple-choice questions and in Section II–Part A free-response questions.
• You are permitted to use the following 4 built-in capabilities of your graphing calculator to obtain an answer:
1. plotting the graph of a function
2. finding the zeros of a function
3. calculating numerically the derivative of a function
4. calculating numerically the value of a definite integral
For example, if you have to find the area of a region, you need to show a definite integral. You may then proceed to use the calculator to produce the numerical value of the definite integral without showing any supporting work. All other capabilities of your calculator can only be used to check your answer. For example, you may not use the built-in [Inflection ] function of your calculator to find points of inflection. You must use calculus showing derivatives and indicating a change of concavity.
• You may not use calculator syntax to substitute for calculus notations. For example, you may not write “Volume = 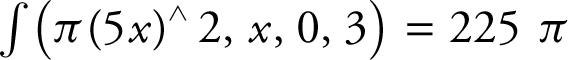 ”; instead you need to write “Volume =
”; instead you need to write “Volume = 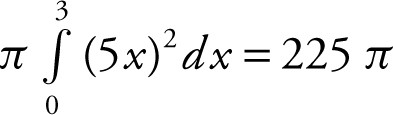 .”
.”
• When using a graphing calculator to solve a problem, you are required to write the setup that leads to the answer. For example, if you are finding the volume of a solid, you must write the definite integral and then use the calculator to compute the numerical value, e.g., Volume = 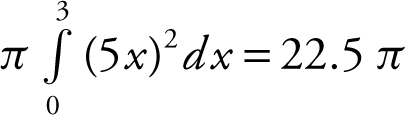 . Simply indicating the answer without writing the integral is considered an incomplete solution, for which you would receive minimal credit (possibly 1 point) instead of full credit for a complete solution.
. Simply indicating the answer without writing the integral is considered an incomplete solution, for which you would receive minimal credit (possibly 1 point) instead of full credit for a complete solution.
• Set your calculator to radian mode, and change to degree mode only if necessary.
• If you are using a TI-89 graphing calculator, clear all previous entries for variables a through z before the AP Calculus exam.
• You are permitted to store computer programs in your calculator and use them in the AP Calculus exam. Your calculator memories will not be cleared.
• Using the [Trace ] function to find points on a graph may not produce the required accuracy. Most graphing calculators have other built-in functions that can produce more accurate results. For example, to find the x -intercepts of a graph, use the [Zero ] function, and to find the intersection point of two curves, use the [Intersection ] function.
• When decimal numbers are involved, do not round until the final answer. Unless otherwise stated, your final answer should be accurate to three places after the decimal point.
• You may bring up to two calculators to the AP Calculus exam.
• Replace old batteries with new ones and make sure that the calculator is functioning properly before the exam.
4.4 Taking the Exam
What Do I Need to Bring to the Exam?
• Several Number 2 pencils.
• A good eraser and a pencil sharpener.
• Two black or blue pens.
• One or two approved graphing calculators with fresh batteries. (Be careful when you change batteries so that you don’t lose your programs.)
• A watch.
• An admissions card or a photo I.D. card if your school or the test site requires it.
• Your Social Security number.
• Your school code number if the test site is not at your school.
• A simple snack if the test site permits it . (Don’t eat anything you haven’t eaten before. You might have an allergic reaction.)
• A light jacket if you know that the test site has strong air conditioning.
• Do not bring Wite Out or scrap paper.
Tips for Taking the Exam

General Tips
• Write legibly.
• Label all diagrams.
• Organize your solution so that the reader can follow your line of reasoning.
• Use complete sentences whenever possible. Always indicate what the final answer is.

More Tips
• Do easy questions first.
• Write out formulas and indicate all major steps.
• Never leave a question blank, especially a multiple-choice question, since there is no penalty for incorrect answers.
• Be careful to bubble in the right grid, especially if you skip a question.
• Move on. Don’t linger on a problem too long. Make an educated guess.
• Go with your first instinct if you are unsure.

Still More Tips
• Indicate units of measure.
• Simplify numeric or algebraic expressions only if the question asks you to do so.
• Carry all decimal places and round only at the end.
• Round to 3 decimal places unless the question indicates otherwise.
• Watch out for different units of measure, e.g., the radius, r , is 2 feet, find 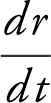 in inches per second.
in inches per second.
• Use calculus notations and not calculator syntax, e.g., write ∫ x 2 dx and not ∫ (x ^2, x ).
• Use only the four specified capabilities of your calculator to get your answer: plotting graphs, finding zeros, calculating numerical derivatives, and evaluating definite integrals. All other built-in capabilities can only be used to check your solution.
• Answer all parts of a question from Section II even if you think your answer to an earlier part of the question might not be correct.

Enough Already … Just 3 More Tips
• Be familiar with the instructions for the different parts of the exam. Review the practice exams in the back of this book.
• Get a good night’s sleep the night before.
• Have a light breakfast before the exam.