5 Steps to a 5: AP Physics 2: Algebra-Based 2024 - Jacobs Greg 2023
STEP 4 Review the Knowledge You Need to Score High
11 Electric Force, Field, and Potential
IN THIS CHAPTER
Summary: Objects are made of atoms, which in turn are made of electrons, protons, and neutrons. An excess of electrons will cause an object to be negatively charged, while an excess of protons will create positively charged objects. This chapter focuses on how to deal with electric charges that aren’t moving through circuit components, hence the name, electrostatics.
An electric field provides a force on a charged particle. Electric potential, also called voltage, provides energy to a charged particle. Once you know the force or energy experienced by a charged particle, Newtonian mechanics (i.e., kinematics, conservation of energy, etc.) can be applied to predict the particle’s motion.
Key Ideas
Electrons and protons are real particles that can move from place to place, or transfer from object to object by contact, but the net charge of the system always stays the same (conservation of charge).
Most objects have the same number of electrons and protons. Only objects with excess protons or electrons have a net charge.
Conductive objects that touch will transfer their charge so that they share any excess charge.
One object can be charged even without touching another charged object, through a process called induction.
A neutral object can have an excess of protons on one side and an excess of electrons on the other side. This charge separation is called charge polarization.
The electric force on a charged particle is qE, regardless of what produces the electric field. The electric potential energy of a charged particle is qV.
Positive charges are forced in the direction of an electric field; negative charges, experience a force in the opposite direction of the field.
Positive charges are forced from high to low electric potential; negative charges are forced from low to high electric potential.
Point charges produce non-uniform electric fields around themselves. Parallel plates produce a uniform electric field between the two oppositely charged plates.
Electric field is a vector, and electric potential is a scalar.
Capacitors store both electric charge and electric potential energy.
Relevant Equations
Electric Charge
Electricity literally holds the world together. Sure, gravity is pretty important, too, but the primary reason that the molecules in your body stick together is because of electric forces. A world without electrostatics would be no world at all.
All matter is made up of three types of particles: protons, neutrons, and electrons. Protons have an intrinsic property called “positive charge.” Neutrons don’t contain any charge, and electrons have a property called “negative charge.”
The unit of charge is the coulomb, abbreviated C. One proton has a charge of 1.6 × 10−19 coulombs. One electron has a charge of —1.6 × 10—19 C.
Most objects that we encounter in our daily lives are electrically neutral—things like couches, for instance, or trees, or bison. These objects contain as many positive charges as negative charges. In other words, they contain as many protons as electrons.
When an object has more protons than electrons, though, it is described as “positively charged”; and when it has more electrons than protons, it is described as “negatively charged.” The reason that big objects like couches and trees and bison don’t behave like charged particles is because they contain so many bazillions of protons and electrons that an extra few here or there won’t really make much of a difference. So even though they might have a slight electric charge, that charge would be much too small, relatively speaking, to detect.
Tiny objects, like atoms, more commonly carry a measurable electric charge, because they have so few protons and electrons that an extra electron, for example, would make a big difference. Of course, you can have very large charged objects. When you walk across a carpeted floor in the winter, you pick up lots of extra charges and become a charged object yourself . . . until you touch a doorknob, at which point all the excess charge in your body travels through your finger and into the doorknob, causing you to feel a mild electric shock.
Electric charges follow a simple rule: Like charges repel; opposite charges attract. Two positively charged particles will try to get as far away from each other as possible, while a positively charged particle and a negatively charged particle will try to get as close as possible.
Let’s take these ideas a step further.
Quanta of Charge, Conservation of Charge, and How Charge Moves Around
First, notice that charge comes in the smallest possible package, a quanta, of one proton or one electron, ±1.6 × 10—19 C. In our everyday world, you can’t get a charge smaller than that. Every charged object comes in multiples of this quanta. You can have objects with a charge of −3.2 × 10—19 C = 2(−1.6 × 10—19 C) = 2 quanta of charge. But you can’t have −4.0 × 10—19 C = 2.5(−1.6 × 10—19 C) = 2.5 quanta of charge, because there is no such thing as half of an electron. It’s just like how money is quantized! You can’t have half of a penny.
Second, atoms have a nuclear structure where the protons are buried deep inside with the electrons zipping around far away on the outside. Electrons are easy to remove or add to atoms. Moving protons in or out of an atom requires nuclear reactions! In the study of static electricity, we are not adding or removing protons from an object. (We discuss nuclear physics in Chapter 15.) So, when an object is negatively charged, it’s because it has too many electrons placed on it. When positively charged, it has lost some electrons.
Third, we must obey the law of conservation of charge. Charge is carried by real things—electrons and protons don’t just appear or disappear. Thus, charge can move around, but the initial charge of the system before will always equal the charge of the system after.
Fourth, how do we move charge around? Remember chemistry? Those atoms on the left side of the periodic table lose their outer electrons easily and can become positive ions. They are metals and good conductors of charge. Those atoms on the right side of the periodic table tend to hold on to their electrons more tightly. In fact, they may even steal electrons from others and become negative ions. These are nonmetals and insulators. Conductors allow charge to easily move through them. Insulators do not let charges move easily but hold them in place where they are.
There are really three ways for an object as a whole to become charged.
1. Charging by Friction
Charging by friction is one that you are probably familiar with. Place two materials into contact that have a different pull on their outer electrons, and electrons start jumping from one object to the other. Rub the objects together and the process speeds up. You have seen this when you comb your hair. Electrons jump from your hair to the comb. Your hair becomes positively charged and the comb negatively charged, but the net charge of the hair-comb system is still zero.
2. Charging by Contact or Conduction
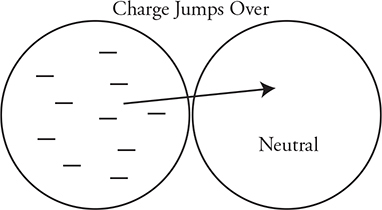
Let’s say we have an object with extra electrons and we touch it to a neutral object. The extra electrons repel each other and some move onto the neutral object. They share the excess charge and become charged with the same sign. If they are the same size, they both get equal amounts of the charge. If one is bigger, it will end up with more charge than the smaller object because there is more room for the charges to spread out.
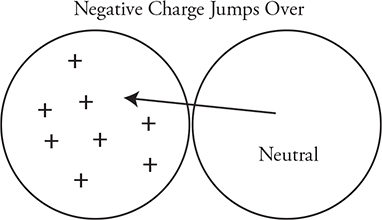
What if the charged object is positively charged? Positives can’t jump to the neutral object because they are buried in the nucleus. In this case, negatives are attracted to the positive object, causing it to become less positive and the neutral object to become positive. It looks like positive charges moved to the right, but in reality negative charges moved to the left. So, sometimes we will say things like “positive charge moved from object A to object B,” but in reality negative electrons moved in the reverse direction from object B to object A.
One last comment on contact: remember that insulators do not let charge move very easily. So, if you touch a charged insulator, you will share only the tiny amount of charge right where you touched it because the rest of the charges on the object are locked in place.
3. Induced Charge, Polarization, and Induction
You can also have something called “induced charge.” An induced charge occurs when an electrically neutral object becomes polarized—when negative charges pile up in one part of the object and positive charges pile up in another part of the object. The drawing below illustrates how you can create an induced charge in an object.
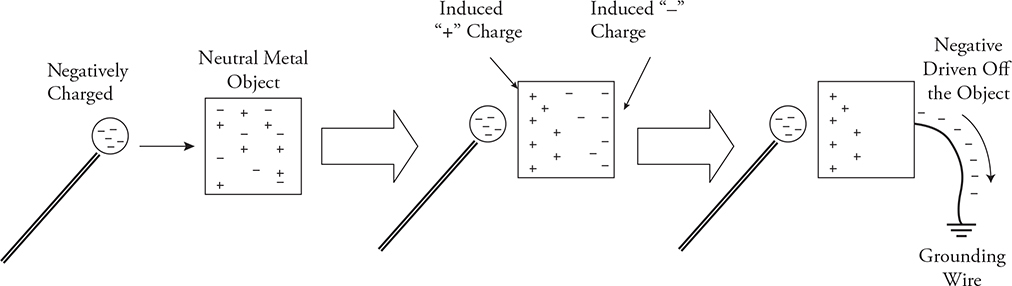
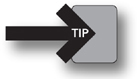
If we supply an escape route, like a grounding wire, for the induced charge piled up on the right, the negative charge will be driven completely off the object, leaving it with a net positive charge. Then disconnect the escape route, and like magic, we just gave the object a permanent positive charge by the process called induction. Note that the negatively charged sphere was brought close to, but did not touch, the neutral metal object! Make sure you understand this process of polarization and induction, as it is likely to show up on the exam.
Charge Distribution on Different Objects
You already know that like charges repel each other, but on an insulator they can’t move. Therefore, a net charge will be stuck where it is. See the figure below. On conductors, any excess charge will force itself to the outside surface. For a uniformly shaped object, like a sphere, the excess charges are going to distribute themselves around the outside of the body evenly. But what if the body has an irregular shape? The excess charges will be forced to the farthest edges in an effort to get as far away from each other as possible. Charge will bunch up disproportionately on any pointy areas the body might have. The key idea to remember is, all the excess charge is on the outside surface of a conductor no matter what the shape is. There will be no excess charge inside a conductor.
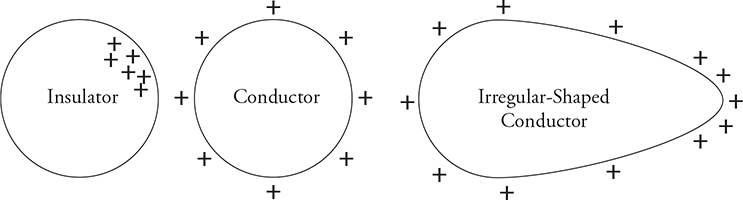
Electric Fields
Before talking about electric fields, I’ll first define what a field, in general, is.
Field: A property of a region of space that can apply a force to objects found in that region of space.
A gravitational field is a property of the space that surrounds any massive object. There is a gravitational field that you are creating and which surrounds you, and this field extends infinitely into space. It is a weak field, though, which means that it doesn’t affect other objects very much—you’d be surprised if everyday objects started flying toward each other because of gravitational attraction. The Earth, on the other hand, creates a strong gravitational field because of its tremendous mass. Objects are continually being pulled toward the Earth’s surface due to gravitational attraction. However, the farther you get from the center of the Earth, the weaker the gravitational field and, correspondingly, the weaker the gravitational attraction you would feel.
An electric field is a bit more specific than a gravitational field: it affects only charged particles.
Electric Field: A property of a region of space that applies a force to charged objects in that region of space. A charged particle in an electric field will experience an electric force.
Unlike a gravitational field, an electric field can either push or pull a charged particle, depending on the charge of the particle. Electric field is a vector; so, electric fields are always drawn as arrows.
Every point in an electric field has a certain value called, surprisingly enough, the “electric field strength,” or E, and this value tells you how strongly the electric field at that point would affect a charge. The units of E are newtons/coulomb, abbreviated N/C.
Force of an Electric Field
The force felt by a charged particle in an electric field is described by a simple equation:
In other words, the force felt by a charged particle in an electric field is equal to the charge of the particle, q, multiplied by the electric field strength, E.
The direction of the force on a positive charge is in the same direction as the electric field; the direction of the force on a negative charge is opposite the electric field.
Let’s try this equation on for size. Here’s a sample problem:
An electron, a proton, and a neutron are each placed in a uniform electric field of magnitude 60 N/C, directed to the right. What is the magnitude and direction of the force exerted on each particle?
The solution here is nothing more than plug-and-chug into 
. Notice that we’re dealing with a uniform electric field—the electric field vector lines are evenly spaced throughout the whole region AND all the electric field vectors are the same length. This means that, no matter where a particle is within the electric field, it always experiences an electric field of exactly 60 N/C.
Also note our problem-solving technique. To find the magnitude of the force, we plug in just the magnitude of the charge and the electric field—no negative signs allowed! To find the direction of the force, use the reasoning presented earlier (positive charges are forced in the direction of the E field, negative charges opposite the E field).
Let’s start with the electron, which has a charge of 1.6 × 10−19 C (no need to memorize; you can look this up on the constant sheet):
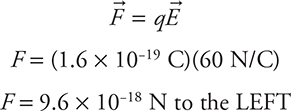
Now the proton:
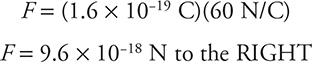
And finally the neutron:
Notice that the proton feels a force in the direction of the electric field, but the electron feels the same force in the opposite direction of the electric field.
Don’t state a force with a negative sign. Signs just indicate the direction of a force, anyway. So, just plug in the values for q and E, then state the direction of the force in words.
Electric Field Vector Diagrams
If we draw an electric field vector on a grid to represent both the direction and strength of the electric field at that point, we would get an electric field vector diagram. This is a visual picture that helps us see the force field as a whole. Place a proton at point A and it will receive a force to the right. Place the proton at point B and it will receive a smaller force to the right because, as we can see, the electric field is weaker. What would an electron experience if we place it at point C? A force down and to the left in the opposite direction of the E-Field because it is negative! Using the length of the electric field vectors as a guide, the magnitude of the electric field strength at these three points ranks in this order: (Greatest) EA > EC > EB (Weakest).
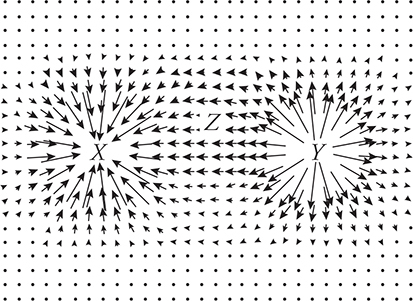
Look at the electric vector field in the next figure. What is going on at points X and Y? Electric field arrows are pointing inward toward X and are getting bigger as they get closer. X must be a negative charge location. Y must be a positive charge location. What direction is the electric field at Z? That’s easy—to the left. What’s the direction of the force on a charge placed at Z? Careful, it’s a trick question! Is it a positive or negative charge? If it is negative, it gets pushed to the right. If it’s positive, it gets forced to the left.
Electric Potential
When you hold an object up over your head, that object has gravitational potential energy. If you were to let it go, it would fall to the ground.
Similarly, a charged particle in an electric field can have electrical potential energy. For example, if you held a proton in your right hand and an electron in your left hand, those two particles would want to get to each other. Keeping them apart is like holding that object over your head; once you let the particles go, they’ll travel toward each other just like the object would fall to the ground.
In addition to talking about electrical potential energy, we also talk about a concept called electric potential.
Electric Potential: Potential energy provided by an electric field per unit charge; also called voltage.
Electric potential is a scalar quantity. The units of electric potential are volts. 1 volt = 1 J/C.
Just as we use the term “zero of potential” in talking about gravitational potential, we can also use that term to talk about voltage. We cannot solve a problem that involves voltage unless we know where the zero of potential is. Often, the zero of electric potential is called “ground.”
Unless it is otherwise specified, the zero of electric potential is assumed to be far, far away. This means that if you have two charged particles and you move them farther and farther from each another, ultimately, once they’re infinitely far away from each other, they won’t be able to feel each other’s presence.
The electrical potential energy of a charged particle is given by this equation:
Here, q is the charge on the particle, and ΔV is the difference in electric potential.
It is extremely important to note that electric potential and electric field are not the same thing. This example should clear things up:
Three points, labeled A, B, and C, are found in a uniform electric field. At which point will a proton have the greatest electrical potential energy?
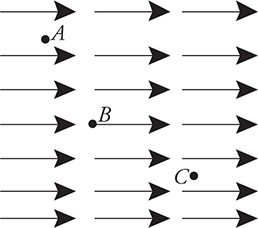
Electric field lines point in the direction that a positive charge will be forced, which means that our proton, when placed in this field, will be pushed from left to right. So, just as an object in Earth’s gravitational field has greater potential energy when it is higher off the ground (think “mgh”), our proton will have the greatest electrical potential energy when it is farthest from where it wants to get to. The answer is A.
I hope you noticed that, even though the electric field was the same at all three points, the electric potential was different at each point.
How about another example?
A positron (a positively charged version of an electron) is given an initial velocity of 6 × 106 m/s to the right. It travels into a uniform electric field, directed to the left. As the positron enters the field, its electric potential is zero. What will be the electric potential at the point where the positron has a speed of 1 × 106 m/s?
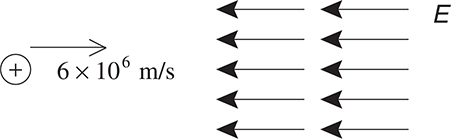
This is a rather simple conservation of energy problem, but it’s dressed up to look like a really complicated electricity problem.
As with all conservation of energy problems, we’ll start by writing our statement of conservation of energy.
Next, we’ll fill in each term with the appropriate equations. Here the potential energy is not due to gravity (mgh), nor due to a spring 
. The potential energy is electric; so it should be written as qV.
Finally, we’ll plug in the corresponding values. The mass of a positron is exactly the same as the mass of an electron, and the charge of a positron has the same magnitude as the charge of an electron, except a positron’s charge is positive. Both the mass and the charge of an electron are given to you on the constants sheet. Also, the problem told us that the positron’s initial potential Vi was zero.
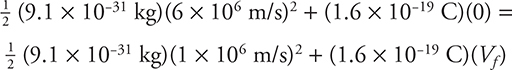
Solving for Vf, we find that Vf is about 100 V.
For forces, a negative sign simply indicates direction. For potentials, though, a negative sign is important. −300 V is less than −200 V, so a proton will seek out a −300 V position in preference to a −200 V position. Positive charges will naturally try to move to more negative electric potential locations. Negative charges will naturally try to move to more positive electric potential locations. So, be careful to use proper + and − signs when dealing with potential.
Equipotential Isolines
Just as you can draw electric field lines, you can also draw equipotential lines.
Equipotential Lines: Lines that illustrate every point at which a charged particle would experience the same potential.
The following figure shows a few examples of equipotential lines (shown with solid lines) and their relationship to electric field lines (shown with arrows):
In the lefthand figure, the electric field points away from the positive charge. At any particular distance away from the positive charge, you would find an equipotential line that circles the charge—we’ve drawn two, but there are an infinite number of equipotential lines around the charge. If the potential of the outermost equipotential line that we drew was, say, 10 V, then a charged particle placed anywhere on that equipotential line would experience a potential of 10 V.
In the righthand figure, we have a uniform electric field. Notice how the equipotential lines are drawn perpendicular to the electric field lines. In fact, equipotential lines are always drawn perpendicular to electric field lines, but when the field lines aren’t parallel (as in the drawing on the left), this fact is harder to see.
Moving a charge from one equipotential line to another takes energy. Just imagine that you had an electron and you placed it on the innermost equipotential line in the drawing on the left. If you then wanted to move it to the outer equipotential line, you’d have to push pretty hard, because your electron would be trying to move toward, and not away from, the positive charge in the middle.
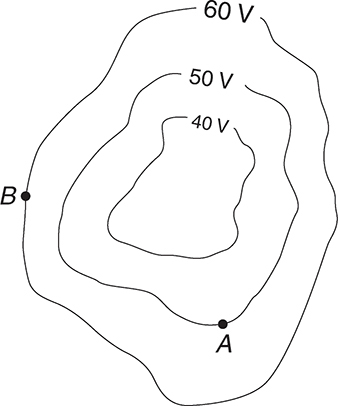
In the diagram above, point A and point B are separated by a distance of 30 cm. How much work must be done by an external force to move a proton from point A to point B?
The potential at point B is higher than at point A; so moving the positively charged proton from A to B requires work to increase the proton’s potential energy. The question here really is asking how much more potential energy the proton has at point B.
Well, potential energy is equal to qV; here, q is 1.6 × 10−19 C, the charge of a proton. The potential energy at point A is (1.6 × 10−19 C)(50 V) = 8.0 × 10−18 J; the potential energy at point B is (1.6 × 10−19 C)(60 V) = 9.6 × 10−18 J. Thus, the proton’s potential is 1.6 × 10−18 J higher at point B, so it takes 1.6 × 10−18 J of work to move the proton there.
Um, didn’t the problem say that points A and B were 30 cm apart? Yes, but that’s irrelevant. Since we can see the equipotential lines, we know the potential energy of the proton at each point; the distance separating the lines is irrelevant.
Look again at the figure. Notice how it looks like a topographical map that shows isolines of constant elevation. A plot of equipotential is just like that, except it shows isolines of equal potential. Positive charges will naturally be forced by the electric field to regions of more negative potential. Negative charges are forced by the electric field toward regions of higher or more positive potential. The flip side of this is that it takes work to “lift” a positive charge to a higher and more positive potential. It takes work to “lift” a negative charge to a more negative potential.
But, what happens if the charged object moves to a location of lower electric potential energy? Just like a falling ball picks up speed as it loses gravitational potential energy and gains kinetic energy, charged objects gain kinetic energy when they move to lower electric potential energy locations.
Example
A proton is accelerated from rest through an electric potential difference of 2000 V. Find the final speed of the proton.
A good idea is to list everything we know. We might not need all that data, but it is nice to have it all in one spot. Since it is a proton, we know its mass and charge:
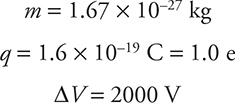
When dealing with voltage, you are going to be solving an energy conservation problem:
Since there is no initial kinetic energy, the equation becomes:
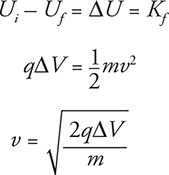
Since you know that kinetic energy is in joules, your potential energy needs to be in joules. Your charge must be in coulombs and electric potential difference is in volts:
Practice
The figure below shows isolines of constant electric potential.
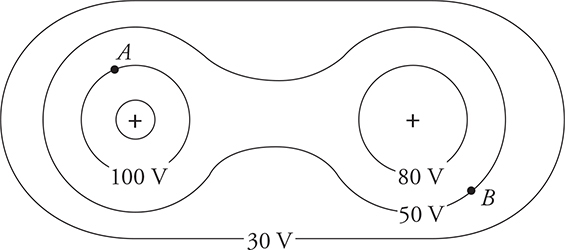
(a) Which way does the electric field vector point at A?
(b) If we place an electron at point A, in which direction will it receive a force?
(c) Does the electron gain or lose energy when it moves from point A to point B?
Answers to the Practice Problem:
(a) Remember that electric field vectors are always perpendicular to the isopotential lines, and directed away from positive charges. So, the electric field vector will be pointing mostly up and a little to the left.
(b) An electron is negative. It will experience a force in the opposite direction to the electric field, so mostly down and to the right—toward the positive charge.
(c) Keep in mind that positive charges want to move to lower electric potentials and negative charges want to move toward higher electric potentials. Since I am moving from 100 V to 50 V, I am moving a negative charge to a lower electric potential. That’s the opposite of what the electron is going to naturally want, so I would have to add energy to the system. Left on its own, the electron would naturally ”fall” toward one of the two positive charges. So we have to do work on the electron to move it from point A to point B. Notice how we cannot neglect the signs when considering the energy problem below.
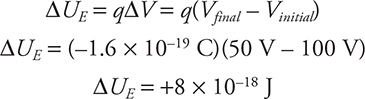
Since the potential energy increased, there had to be work done on the electron.
Special Geometries for Electrostatics
There are two situations involving electric fields that are particularly nice because they can be described with some relatively easy formulas. Let’s take a look.
Parallel Plates
If you take two metal plates, charge one positive and one negative, and then put them parallel to each other, you create a uniform electric field in the middle, as shown below.
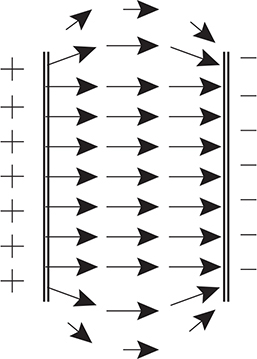
The electric field between the plates has a magnitude of
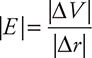
ΔV is the voltage difference between the plates, and r is the distance between the plates. Notice how the electric field is uniform in strength and direction near the center of the capacitor away from the edges. Near the edges of the capacitor, the electric field weakens and bends as shown in the figure.
Charged parallel plates can be used to make a capacitor, which is a charge-storage device. When a capacitor is made from charged parallel plates, it is called, logically enough, a “parallel-plate capacitor.”
The battery in the following figure provides a voltage across the plates; once you’ve charged the capacitor, you disconnect the battery. The space between the plates prevents any charges from jumping from one plate to the other while the capacitor is charged. When you want to discharge the capacitor, you just connect the two plates with a wire.
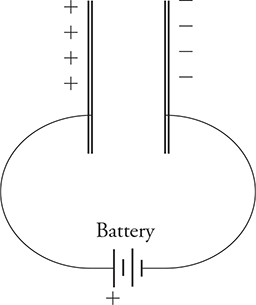
The amount of charge that each plate can hold is described by the following equation:
Q is the charge on each plate, C is called the “capacitance,” and ΔV is the voltage across the plates. The capacitance is a property of the capacitor you are working with, and it is determined primarily by the size of the plates and the distance between the plates. The units of capacitance are farads, abbreviated F; 1 coulomb/volt = 1 farad.
The only really interesting thing to know about parallel-plate capacitors is that their capacitance can be easily calculated. The equation is:
In this equation, A is the area of each plate (in m2), and d is the distance between the plates (in m). The term e0 (pronounced “epsilon-naught”) is called the “vacuum permittivity.” The value of e0 is 8.85 × 10−12 C/V·m, which is listed on the constants sheet.
κ is the dielectric constant. This is essentially how good of an insulator you have between the capacitor plates (κvacuum = κair = 1.0). Higher numbers mean a better insulator than a vacuum/air. When κ gets large the capacitance of the capacitor goes up, meaning it can store more charge for the same amount of potential difference.
Point Charges
As much as the writers of the AP exam like parallel plates, they love point charges. So you’ll probably be using these next equations on the test.
But, please don’t go nuts . . . the formulas for force on a charge in an electric field 
and a charge’s electrical potential energy (ΔUE = qΔV) are your first recourse, your fundamental tools of electrostatics. Only use the equations in this section when you have convinced yourself that a point charge is creating the electric field or the voltage in question.
First, the value of the electric field at some distance away from a point charge:
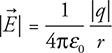
q is the charge of your point charge, 
is called the Coulomb’s law constant 
, and r is the distance away from the point charge. The field produced by a positive charge points away from the charge; the field produced by a negative charge points toward the charge. When finding an electric field with this equation, do NOT plug in the sign of the charge or use negative signs at all.
Second, the electric potential at some distance away from a point charge:
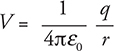
When using this equation, you must include a + or − sign on the charge creating the potential.
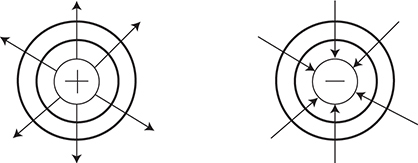
Electric field vectors point away from positive charges and toward negative charges. Equipotential “iso-lines” form circles around isolated point charges as seen in the figure below.
And third, the force that one point charge exerts on another point charge:
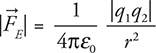
In this equation, q1 is the charge of one of the point charges, and q2 is the charge on the other one. This equation is known as Coulomb’s law.
Practice
To get comfortable with these three equations, here is a rather comprehensive problem.
Yikes! This is a monster problem. But if we take it one part at a time, you’ll see that it’s really not too bad.
Part 1—Electric Field
Electric field is a vector quantity. So we’ll first find the electric field at point P due to charge A, then we’ll find the electric field due to charge B, and then we’ll add these two vector quantities. One note before we get started: to find r, the distance between points P and A or between P and B, we’ll have to use the Pythagorean theorem. We won’t show you our work for that calculation, but you should if you were solving this on the AP exam.
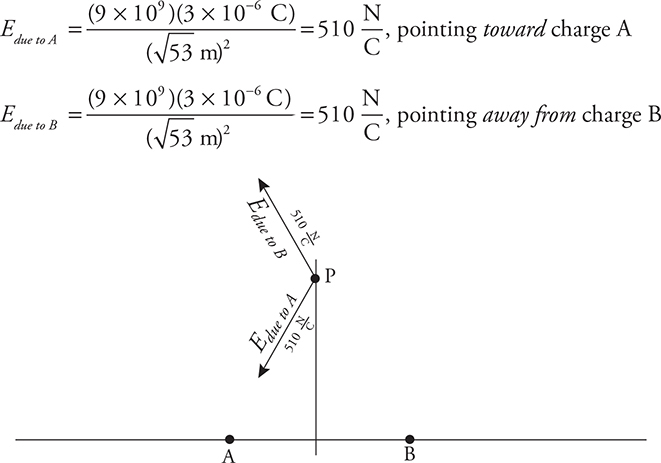
Note that we didn’t plug in any negative signs! Rather, we calculated the magnitude of the electric field produced by each charge, and showed the direction on the diagram.
Now, to find the net electric field at point P, we must add the electric field vectors. This is made considerably simpler by the recognition that the y-components of the electric fields cancel . . . both of these vectors are pointed at the same angle, and both have the same magnitude. So, let’s find just the x-component of one of the electric field vectors:
Ex = E cos θ, where θ is measured from the horizontal.
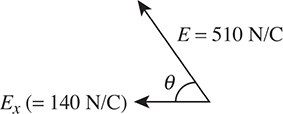
Some quick trigonometry will find cos θ . . . since cos θ is defined as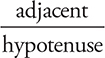 
, inspection of the diagram shows that 
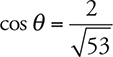. So, the horizontal electric field 
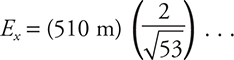this gives 140 N/C.
And now finally, there are TWO of these horizontal electric fields adding together to the left—one due to charge A and one due to charge B. The total electric field at point P, then, is
280 N/C, to the left
Part 2—Force
The work that we put into Part 1 makes this part easy. Once we have an electric field, it doesn’t matter what caused the E field—just use the basic equation 
to solve for the force on the electron, where q is the charge of the electron. So,
The direction of this force must be OPPOSITE the E field because the electron carries a negative charge; so, to the right.
Part 3—Potential
The nice thing about electric potential is that it is a scalar quantity, so we don’t have to concern ourselves with vector components and other such headaches.
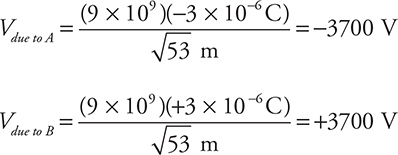
The potential at point P is just the sum of these two quantities. V = zero!
Notice that when finding the electric potential due to point charges, you must include negative signs . . . negative potentials can cancel out positive potentials, as in this example.
Electric Fields Around a Point Charge and a Charged Conducting Sphere
To find the magnitude of the electric field outside a conducting sphere or point charge:
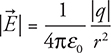
Since the variables are all absolute valued, like Coulomb’s law, and the electric field is a vector, the equation tells you only the magnitude of the electric field, you still need to do a vector diagram and solve for the resultant if there are multiple fields that overlap like in the practice problem above.
Inside a conducting sphere, things get interesting. First of all, any excess charge moves to the outside surface of the sphere. Inside the sphere, there is no electric field, because any charge placed inside the sphere is completely surrounded by the charge on the outside of the sphere. So the net force on any charge placed inside a conducting sphere is zero. If the electric field were graphed, it would look like this:
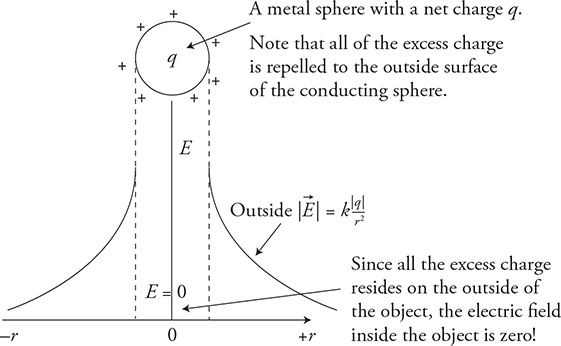
Remember: There will not be an electric field inside a charged conducting object! This is not true for insulating objects, because the excess charge cannot migrate to the outside surface.
Electric Potential Associated with a Point Charge and a Charged Conducting Sphere
To find electric potential outside a single point charge or charged sphere, the electric potential is:
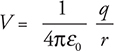
If you need to find the potential due to a group of charges, don’t panic—you are dealing with scalars. Simply solve for the potential from each charge individually and add them all up, like in the practice problem above. Once again, be careful and don’t forget your signs; they are important!
What about inside a charged conducting sphere? We know there is no electric field inside the sphere, so there is no electrical potential difference from one point to another inside the sphere. To find the electrical potential inside the sphere:
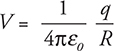
where R is the radius of the sphere. As a graph, electrical potential looks like this:
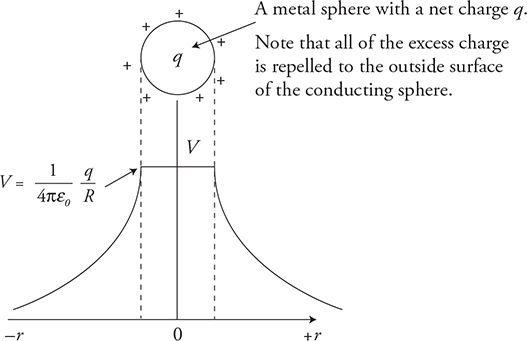
The Force Between Two Charges
Static electricity is nice to us because in many ways it mirrors things we have already learned in AP Physics 1, like gravity. Let’s take a look at the force between two charged particles. The equation for this is Coulomb’s law, and it is:
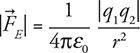
where:
• ε0 is a constant called vacuum permittivity, which is simply a measure of how easily an electric field passes through a vacuum. ε0 = 8.85 × 10—12 C2/N·m2.
• 
is the Coulomb’s law electrostatic constant. 
.
• q1 and q2 are the two charges in coulombs.
• r is the distance between the centers of the bodies.
The AP exam will ask you to compare the electric force to gravity so make sure you know the similarities and differences. Notice how similar Coulomb’s law is to Newton’s law of universal gravitation:
Both are inversely related to the radius squared. But, gravity only attracts while the electric force can attract or repel. Also, the electric force only affects charged objects and is much, much stronger than gravity.
Mechanics and Charges
Many of the behaviors you learned in mechanics will be useful with charged objects.
Newton’s Laws
• Newton’s first law: If the charged object is at rest, then all the forces acting on the change must be canceling out: ΣF = 0.
• If there is a net force on a charge and the charge is free to move, they will follow Newton’s second law: ΣF = ma.
• Newton’s third law: the electric forces between the two charges will be equal but opposite in direction.
• Remember that force is a vector, so you must solve any problem involving multiple electric forces using a free-body diagram and vector analysis.
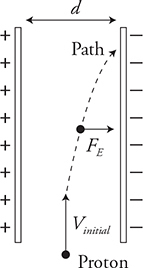
Charges in a Uniform Electric Field
A proton placed between two capacitor plates will accelerate toward the negative plate and away from the positive plate. But, if the proton is shot between the plates, it will experience parabolic trajectory motion just like a football in a gravitational field. In the following diagram, a proton accelerates to the right. The force on the charge is FE = qE = qΔV/d. And the acceleration of the charge will be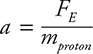 
. Remember that electrons will accelerate in the opposite direction of the electric field!
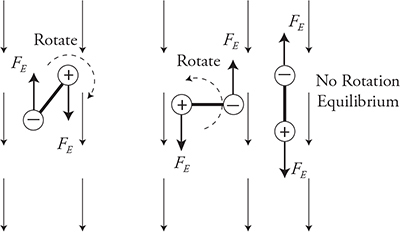
• An electric dipole, in a uniform electric field, will receive a torque that will cause it to rotate back and forth as it tries to align with the field. If the dipole has two opposite changes of equal size, it will not translate, because the two forces on each charge are equal and opposite in direction. See the following figure.
Conservation of Momentum Applied to Charges
• When charges attract, they can collide. Look at the next diagram. Charge A is negative and charge B is positive. Both charges start at rest.
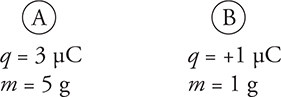
(a) Which receives the larger force? Newton’s third law—the force is the same.
(b) Which accelerates the greatest? B because of its smaller mass.
(c) What is the momentum of the system right before they collide? Conservation of momentum says it will be zero because they began with zero momentum.
(d) Where will they collide? They will collide closer to A. A has a larger mass and a smaller acceleration to the right. B has a smaller mass and a larger acceleration to the left. They will collide at the center of mass of the system.
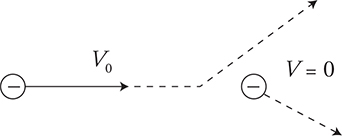
• Charged particles can interact in a momentum collision without even touching. An electron shot at a stationary electron can “bounce off” due to the electrostatic repulsion and not even touch the other. Conservation of momentum is still in play. Both the x and y momentums before the interaction and after the interaction must be conserved.
❯ Practice Problems
Multiple Choice
Questions 1 and 2
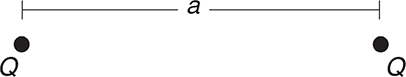
Two identical positive charges Q are separated by a distance a, as shown above.
1. What is the electric field at a point halfway between the two charges?
(A) 4 kQ/a2
(B) 2 kQ/a2
(C) zero
(D) 8 kQ/a2
2. What is the electric potential at a point halfway between the two charges?
(A) 2 kQ/a
(B) zero
(C) 4 kQ/a
(D) 8 kQ/a
Questions 3 and 4
The diagram above shows two parallel metal plates that are separated by distance d. The potential difference between the plates is V. Point A is twice as far from the negative plate as is point B.
3. Which of the following statements about the electric potential between the plates is correct?
(A) The electric potential is the same at points A and B.
(B) The electric potential is two times larger at A than at B.
(C) The electric potential is two times larger at B than at A.
(D) The electric potential is four times larger at B than at A.
4. Which of the following statements about the electric field between the plates is correct?
(A) The electric field is the same at points A and B.
(B) The electric field is two times larger at A than at B.
(C) The electric field is two times larger at B than at A.
(D) The electric field is four times larger at B than at A.
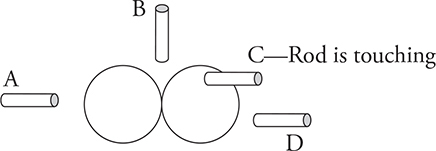
5. Two identical neutral metal spheres are touching as shown in the figure. Which of the following locations of a positively charged insulating rod will create the largest positive charge in the sphere on the right?
6. A student is comparing the gravitational field of a planet and the electric field of a positively charged metal sphere. Which of the following correctly describes the two fields?
(A) Both fields increase in magnitude as the size of the object creating the field increases.
(B) Both fields are proportional to 1/radius.
(C) Both fields are directed radially but in opposite directions.
(D) Both fields form concentric circles of decreasing strength at larger radii.
7. Three small droplets of oil with a density of r are situated between two parallel metal plates as shown. The bottom plate is charged positive and the top plate is charged negative. All the particles begin at rest. As time passes, particle 1 accelerates downward, particle 2 remains stationary, and particle 3 accelerates upward as shown. Which of the following statements is consistent with these observations?
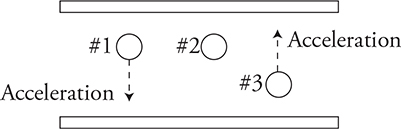
(A) Particle 1 must be negatively charged.
(B) Particle 2 must have no net charge.
(C) Particle 2 has a mass that is too small to affect its motion.
(D) Particle 3 must be positively charged.
8. A student brings a negatively charged rod near an aluminum sphere but does not touch the rod to the sphere. He grounds the sphere and then removes the ground. Which of the following correctly describes the force between the rod and sphere before and after the sphere is grounded?
Questions 9 and 10 refer to the following material.
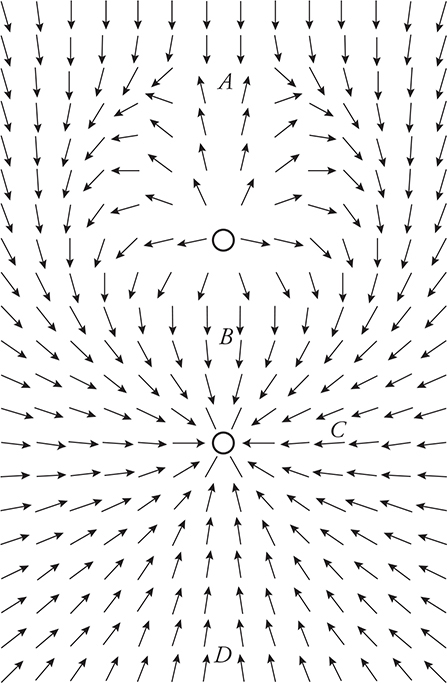
The figure above shows the electric field in a region surrounding two charges. The vectors in the diagram are not scaled to represent the strength of the electric field but show only the direction for the field at that point.
9. At which of the indicated points could you place a positive charge and have it receive the smallest force?
(A) A
(B) B
(C) C
(D) D
10. Which two points have the most similar electric potential?
(A) A and B
(B) B and C
(C) C and D
(D) D and A
11. A balloon rubbed with hair is suspended from the ceiling by a light thread. One at a time, a neutral wooden board and then a neutral steel plate of the same size are brought near to the balloon without touching. Which of the following correctly describes and explains the behavior of the balloon?
(A) The balloon is not attracted to the steel or the wood because both are neutral objects.
(B) The balloon is attracted to the steel because it is a conductor but not to the wood because it is an insulator.
(C) The balloon is attracted equally to both the steel and wood because both become polarized.
(D) The balloon is attracted to the steel more than it is attracted to the wood because steel is a conductor and the wood is an insulator.
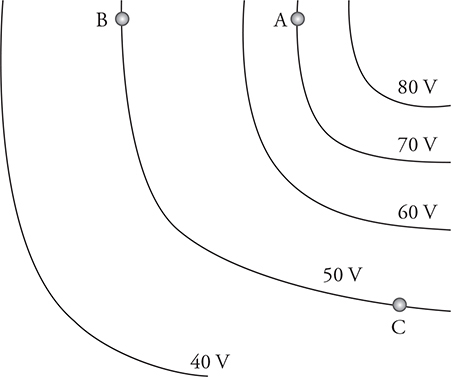
12. The figure shows isolines of electric potential in a region of space. Which of the following will produce the greatest increase in electric potential energy of the particle in the electric field?
(A) Moving an electron from point A to point C
(B) Moving an electron from point B to point A
(C) Moving a proton from point B to point C
(D) Moving a proton from point A to point C
Questions 13—16
The left figure shows a capacitor with a horizontal electric field. The distance between the plates is 4x. The right figure shows two electrons, e1 and e2, and two protons, p1 and p2, which are placed between the plates at the locations shown.
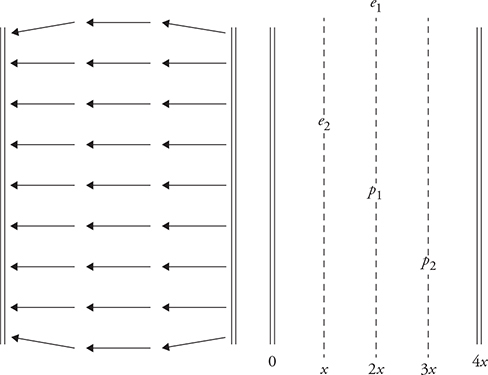
13. Which of the following correctly ranks the electric fields in between the capacitor plates at locations x, 2x, and 3x?
(A) Ex > E2x > E3x
(B) Ex = E2x = E3x
(C) Ex = E3x > E2x
(D) E3x > E2x > Ex
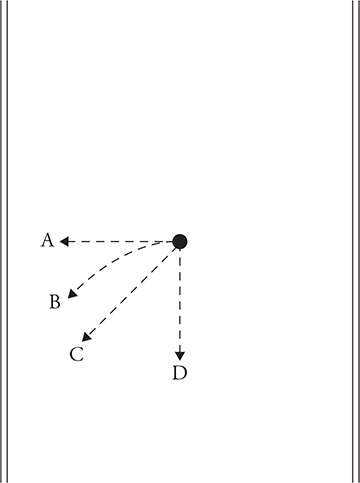
14. Charge p1 is released from rest. Which of the trajectories shown in the figure above is a possible path of the released charge?
(A) A
(B) B
(C) C
(D) D
15. All the particles are released from rest from the locations shown. Assume that all of the particles eventually collide with a capacitor plate. Which particle will achieve the greatest speed before impact with a capacitor plate?
(A) e1
(B) e2
(C) p1
(D) p2
16. After being released from rest, proton p2 attains a final velocity of v just before striking a capacitor plate. Let the mass and charge of the proton be mp and e. The electric potential at locations 0, x, 2x, 3x, and 4x are V0, Vx, V2x, V3x, and V4x, respectively. What is the magnitude of the electric field between the plates? (Select two answers.)
(A)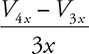 
(B)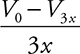 
(C)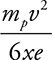 
(D)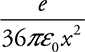 
Free Response
17. Two conducting metal spheres of different radii, as shown above, each have charge −Q.
(A) Consider one of the spheres. Is the charge on that sphere likely to clump together or to spread out? Explain briefly.
(B) Is the charge more likely to stay inside the metal spheres or on the surface of the metal spheres? Explain briefly.
(C) If the two spheres are connected by a metal wire, will charge flow from the big sphere to the little sphere, or from the little sphere to the big sphere? Explain briefly.
(D) Which of the following two statements are correct? Explain briefly.
i. If the two spheres are connected by a metal wire, charge will stop flowing when the electric field at the surface of each sphere is the same.
ii. If the two spheres are connected by a metal wire, charge will stop flowing when the electric potential at the surface of each sphere is the same.
(E) Explain how the correct statement you chose from part (D) is consistent with your answer to (C).
18. A negatively charged piece of clear sticky tape is brought near to, but not into contact with, an aluminum can.
(A) What, if anything, happens to the tape? Explain your reasoning.
(B) A negatively charged balloon that has a charge much larger than that of the clear sticky tape, is brought near the aluminum can without touching. What, if anything, happens to the tape? Explain your reasoning.
19. Your teacher gives you a charged metal sphere that rests on an insulating stand. The teacher asks you to determine if the charge on the object is positive or negative.
(A) List the items you would use to perform this investigation.
(B) Outline the experimental procedure you would use to make this determination. Indicate the measurements to be taken and how the measurements will be used to obtain the data needed. Make sure your outline contains sufficient detail so that another student could follow your procedure and duplicate your results.
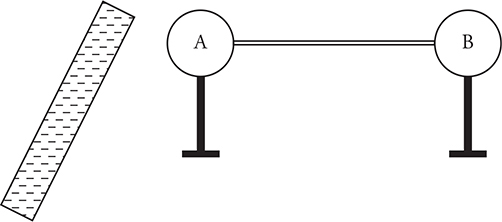
20. The figure above shows two conductive spheres (A and B) connected by a rod. Both spheres begin with no excess charge. A negatively charged rod is brought close to and held near sphere A as shown.
(A) If the connecting rod is made of wood, what is the net charge of the spheres while the rod is held in the position shown? Justify your answer.
(B) If the connecting rod is made of copper, what is the net charge of the spheres while the rod is held in the position shown? Justify your answer.
(C) The rod is now brought into contact with sphere A. How will this change the answers to the previous two questions? Explain.
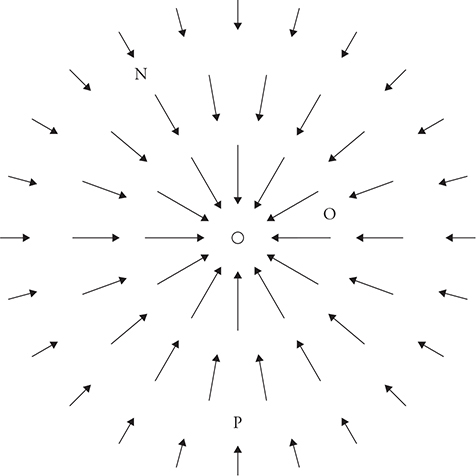
21. The electric field around a charged object is shown in the figure above.
(A) What aspects of the electric field indicate the sign on the charge?
(B) Rank the magnitudes of the electric field at points N, O, and P. Explain what aspects of the diagram indicate the strength of the electric field.
(C) A proton is placed at point P, and an electron is placed at point N. Both are released from rest at the same time. Compare and contrast the acceleration of the two particles at the instant they are released, and explain any differences.
(D) Describe the motions of the proton and the electron for a long time after they are released. Justify your claim.
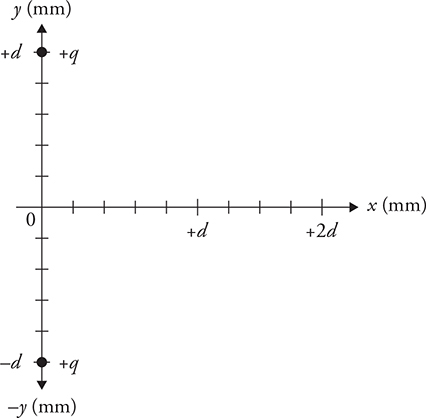
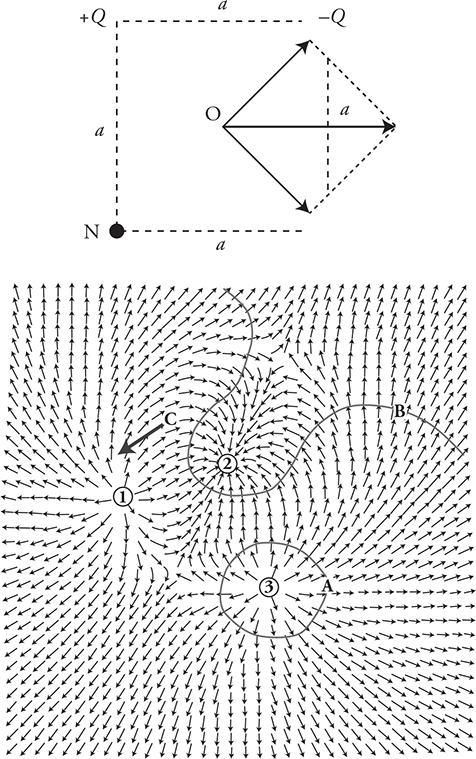
22. Two positive charges (+q) are fixed at +d and —d on the y-axis so they cannot move, as shown in the figure above.
(A) Calculate the force on a third charge, —q, placed at +d on the x-axis. What direction is the force? Show all your work.
(B) If the charge —q is moved to the origin, what will be the new force on the charge? Justify your response.
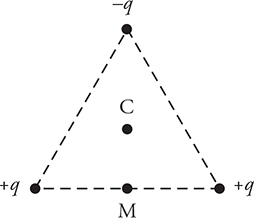
23. Three charges of magnitude q are placed at the corners of an equilateral triangle, as shown in the figure above.
(A) An electron is placed at C, the center of the triangle. Draw a force diagram of all the forces on the electron. All forces should be drawn proportionally. What is the direction of the net force on the electron?
(B) The electron is removed and a proton is placed at M, the midpoint of the bottom side of the triangle. Will the net force on the proton be greater than, less than, or the same as the net force on the electron from part (A) above? Justify your claim.
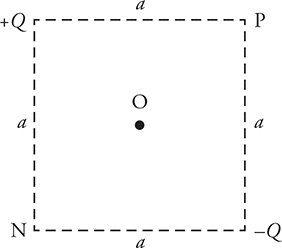
24. Two charges, +Q and —Q, are placed at the corners of a square whose sides have a length of a. Points P and N are located on the corners of the square. Point O is in the center of the square.
(A) Sketch an arrow to indicate the directions of the electric field at points N, O, and P. Make sure the vectors are drawn to the correct proportion.
(B) Calculate the electric potentials at points N, O, and P.
(C) A proton is moved from point P to point O. How much total work is done by the electric field during this move? Explain.
(D) By moving only one of the charges, explain how the electric field at point O can be made to point directly to the right.
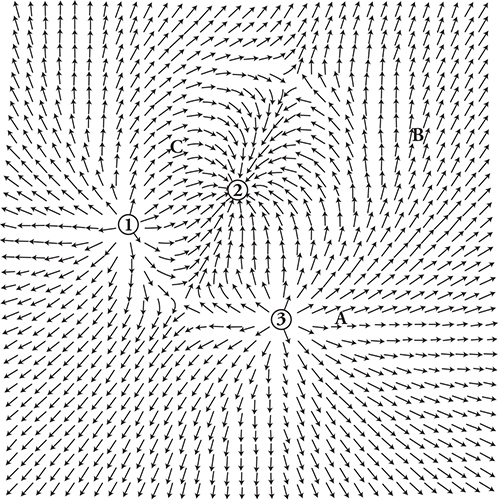
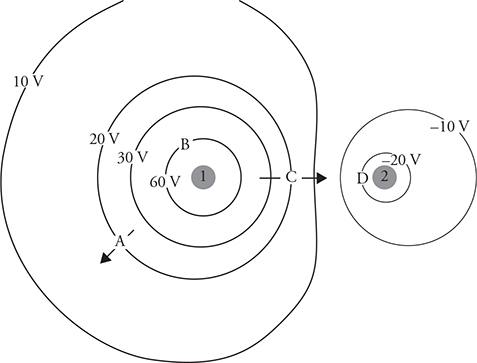
25. Electric field vectors around three charges 1, 2, and 3 are shown in the figure above.
(A) What are the signs of the three charges? Explain what aspects of the electric field indicate the sign of the charges.
(B) Draw the direction of the force on an electron placed at point C.
(C) Sketch two isoline lines of constant electric potential—one that passes through point A and another that passes through point B.
(D) Which isoline has a higher electric potential, the line that passes through point A or the one that passes through point B? Justify your answer.
26. The figure shows isolines of electric potential. Circles 1 and 2 represent two spherical charges. Points A, B, C, and D represent locations on isolines of electric potential.
(A) What are the signs of the two charges, and how do their relative magnitudes compare? Explain how the isolines help you determine this.
(B) A proton is released from point C and moves through an electric potential difference of magnitude 40 V.
i. On which isoline of electric potential will the proton end up?
ii. The proton will have kinetic energy when it arrives at this new isoline. Where does this kinetic energy come from?
a. For the system that includes the two charges and the proton, explain where this kinetic energy comes from.
b. For the system that includes only the proton, explain where this kinetic energy comes from.
(C) An electron at point A is moved to point B. Has the electric potential energy of the electron-charges system increased or decreased? Justify your answer with an equation.
(D) The distance between points C and D is d. Derive a symbolic expression for the magnitude of the average electric field between the two points. Also, indicate the direction of the electric field.
(E) A particle with positive charge of Q is released from point C and gains kinetic energy on its path to point D. Derive a symbolic equation for the amount of work done by the electric field and the final kinetic energy of the proton.
(F) Sketch electric field vectors at points A and C. The vectors should be drawn so their relative strengths are reflected in the drawing.
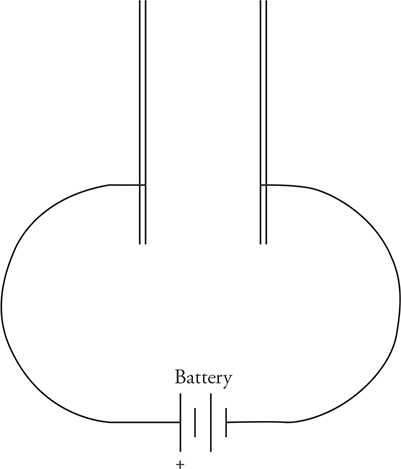
27. A battery of potential difference ΔV is connected to a parallel plate capacitor for a long time. The separation between the plates is d, and the area of one plate is A.
(A) Sketch the electric field between the plates of the capacitor.
(B) Sketch isolines of constant electric potential between the plates.
(C) Write an expression for the electric field strength between the plates.
(D) Write an expression for the charge on the left plate. Show your work.
(E) What is the net charge on both plates combined? Explain.
(F) A proton with a charge of +e is released from the positive plate. Write an expression for the net force on the proton using known quantities. Do you need to include the force of gravity in your calculation? Justify your answer.
(G) Write an expression for the velocity of the proton when it reaches the negative plate. Derive this value using the concept of forces and the concept of energy.
(H) Now a second proton is released from a point midway between the plates. Does this proton reach the negative plate with the same velocity as the first proton that was released from the positive plate? Justify your answer with an equation.
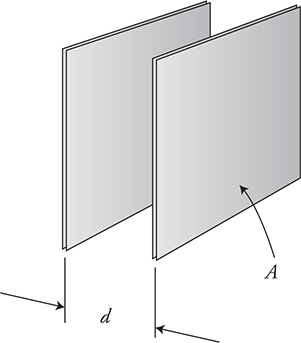
28. A parallel plate capacitor with a capacitance of C is shown in the figure above. The area of one plate is A, and the distance between the plates is d.
(A) If the area of both capacitor plates as well as the distance between them were doubled, what would be the effect on the capacitance of the capacitor? Explain.
(B) The capacitor is connected to a battery of potential difference ΔV. If the potential difference of the battery is doubled, what happens to the charge stored on the plates and the capacitance of the capacitor? Justify your answer.
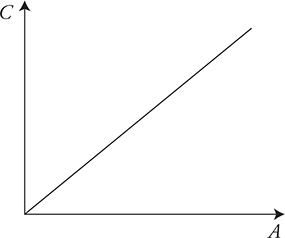
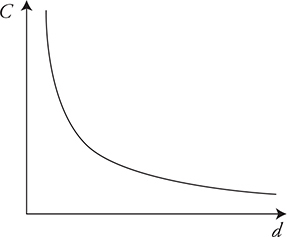
(C) In an experiment, the area (A) of the capacitor plates is changed to investigate the effect on the capacitance (C) of the capacitor. Sketch the graph of the lab data you expect to see from this experiment.
(D) In another experiment, the distance between the plates (d) is changed to investigate the effect on the capacitance (C) of the capacitor. Sketch the graph of the lab data you expect to see from this experiment.
(E) You are going to use a capacitor to power a lightbulb. You need the bulb to shine for a long time. Describe the geometry of the capacitor you would choose to power the bulb. Explain your answer.
❯ Solutions to Practice Problems
1. (C) Electric field is a vector. Look at the field at the center due to each charge. The field due to the left-hand charge points away from the positive charge (i.e., to the right); the field due to the right-hand charge points to the left. Because the charges are equal and are the same distance from the center point, the fields due to each charge have equal magnitudes. So the electric field vectors cancel! E = 0.
2. (C) Electric potential is a scalar. Look at the potential at the center due to each charge: Each charge is distance a/2 from the center point, so the potential due to each is kQ/(a/2), which works out to 2 kQ/a. The potentials due to both charges are positive, so add these potentials to get 4 kQ/a.
3. (B) If the potential difference between plates is, say, 100 V, then we could say that one plate is at +100 V and the other is at zero V. So, the potential must change at points in between the plates. The electric field is uniform and equal to V/d (d is the distance between plates). Thus, the potential increases linearly between the plates, and A must have twice the potential as B.
4. (A) The electric field by definition is uniform between parallel plates. This means the field must be the same everywhere inside the plates.
5. (A) Rods A, B, and D will each polarize the spheres, drawing negative charges toward themselves and leaving the opposite side positively charged. Thus A will cause the right sphere to be the most positive. Touching the spheres with the insulating rod will cause some of the polarized negative charge from the spheres to flow onto the rod. Since the rod is an insulator, this leaves the spheres with only a small excess positive charge that will be shared between both spheres.
6. (C) The magnitude of gravitational 
and electric fields 
depend on the mass and charge of the objects respectively. They are both proportional to 1/r2 and are directed along the radius from the center of mass or center of charge. Gravitational fields always point inward along the radius because it always attracts mass. Electric fields point inward for negative charges and outward for positive charges.
7. (D) All the droplets have mass (m = ρV) and will experience a downward gravitational force. Particle 1 could be uncharged and simply falling due to the force of gravity. Particle 2 must have an electric force to cancel the gravity force. Particle 3 must be positive to receive an electric force upward larger than the force of gravity downward.
8. (A) Before grounding, the negatively charged rod polarized the sphere causing an attraction. After grounding, the sphere has been charged the opposite sign by the process of induction and the two will attract.
9. (A) The electric field vectors indicate that the electric field at location A is zero or very small.
10. (B) Isolines of constant potential are perpendicular to the electric field vectors. B and C appear to be on the same isoline that circles the bottom negative charge.
11. (D) The charged balloon will polarize both the wooden board and the steel plate. Therefore, it will be attracted to both. However, the polarization of the wood occurs on an atomic scale because it is an insulator, and its electrons do not move easily. The steel is a conductor that allows its electrons to migrate. This permits the electrons in the steel to move farther and create a larger charge separation in the process of polarization. This means the balloon will be attracted to the steel more strongly than to the wood.
12. (A) ΔUE = qΔV. To get the greatest increase in electric potential energy, we need the greatest change in electric potential times the charge. The charge of protons and electrons are the same magnitude. To increase the electric potential energy of a proton, we need to move the proton to higher potentials. To increase the electric potential energy of the electron, we need to move the electron to lower electric potentials.
13. (B) The electric field between the plates of a parallel plate capacitor is uniform and constant in strength as long as you are not too close to the edges of the capacitor.
14. (A) The electric force on a positive charge is in the direction of the electric field. The gravity force is much smaller than the electric force. All the other trajectories show gravity stronger than the electric force.
15. (B) Both e2 and p2 will travel through the same distance of 3x, which is also the largest potential difference. Both also receive the same magnitude of electric force. The mass of an electron is much smaller than that of a proton. Therefore, the electron will achieve a greater final velocity.
16. (A) and (C)
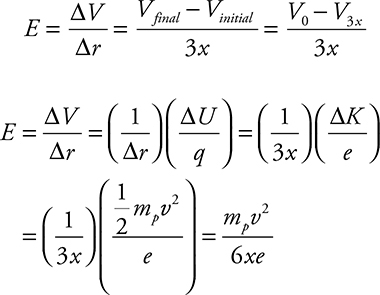
17. (A) Like charges repel, so the charges are more likely to spread out from each other as far as possible.
(B) “Conducting spheres” mean that the charges are free to move anywhere within or onto the surface of the spheres. But because the charges try to get as far away from each other as possible, the charge will end up on the surface of the spheres. This is actually a property of conductors—charge will always reside on the surface of the conductor, not inside.
(C) Charge will flow from the smaller sphere to the larger sphere. Following the reasoning from parts (A) and (B), the charges try to get as far away from each other as possible. Because both spheres initially carry the same charge, the charge is more concentrated on the smaller sphere; so the charge will flow to the bigger sphere to spread out. (The explanation that negative charge flows from low to high potential, and that potential is less negative at the surface of the bigger sphere, is also acceptable here.)
(D) The charge will flow until the potential is equal on each sphere. By definition, negative charges flow from low to high potential. So, if the potentials of the spheres are equal, no more charge will flow.
(E) The potential at the surface of each sphere is −kQ/r, where r is the radius of the sphere. Thus, the potential at the surface of the smaller sphere is initially more negative, and the negative charge will initially flow from low-to-high potential onto the larger sphere.
18. (A) The clear sticky tape is attracted to the can due to charge polarization of the can.
(B) The tape is now repelled by the can because the stronger negative charge of the balloon will drive electrons toward the right side of the can, which will repel the tape.
19. There are several ways to accomplish this lab. Here is one example:
(A) A red balloon and a blue balloon, thread, kitchen plastic wrap, human hair.
(B) Procedure:
1. Blow up the balloons and tie a long thread to each.
2. Charge the red balloon positively by rubbing the kitchen plastic wrap all over its surface. Charge the blue balloon negatively by rubbing its surface on your hair.
3. Hold each balloon by the thread, and one at a time, bring them close to the charged metal sphere. Observe the results. One balloon should be attracted and the other repelled. The balloon that is repelled will be the same sign charge as the metal sphere.
20. (A) Both spheres will remain neutral because there is not a conductive pathway for charge to move onto or off of either sphere.
(B) Due to induction, the system that includes both spheres and the copper rod will become polarized. Sphere A will be positively charged, and sphere B will be negatively charged. The net charge of the system that includes both spheres and the copper rod is still zero because no charge has been added to the system.
(C) The answer to (A) is now: Sphere A becomes negative by contact, but sphere B remains neutral because wood is an insulator. The answer to (B) is now: Both spheres become negative by contact because there is a conductive pathway connecting both spheres.
21. (A) All the electric field vectors in the figure point inward toward the charge. Electric field vectors point in the direction of the force on positive charges; therefore, the charge in the figure is negative.
(B) EO > EN = EP. The length of the electric field vector indicates the strength of the field.
(C) The electric field is the same magnitude at N and P. Both the electron and the proton have the same magnitude of charge. The electric force (FE = Eq) for each is the same. However, the mass of the proton is larger than that of the electron. Therefore, the acceleration of the electron is greater. The electron accelerates in the opposite direction of the field. The proton accelerates in the same direction as the field.
(D) The proton accelerates from rest inward in the direction of the electric field. The acceleration of the proton increases as it moves into a larger electric field closer to the charge. The electron accelerates outward away from the charge. The acceleration decreases as it gets farther away from the charge where the field is weaker. The electron eventually reaches a constant velocity when it is very far away from the charge.
22. (A) See figure. Due to the symmetry of the arrangement of charges the force on —q will be to the left along the x-axis. Only the x-component of the force
needs to be calculated. 
The radius between the charges is: r2 = d2 + d2 = 2d2.
Therefore, the magnitude of the force between +q and —q is.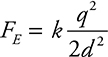 
The x-component of this force is: FEx = FE cos θ.
Where, cos θ is equal to: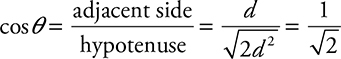
Therefore the x-component of this force becomes: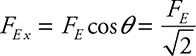 
There are two charges with this force on —q. So the net force on —q is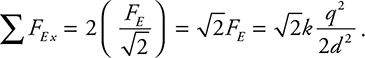 
This net force is in the negative x-direction. See figure.
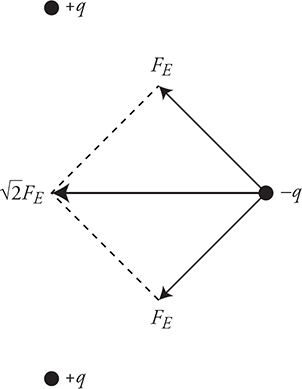
(B) The net force is zero because they are equal in size and opposite in direction. (Always look for any symmetries that will give you a simple answer!)
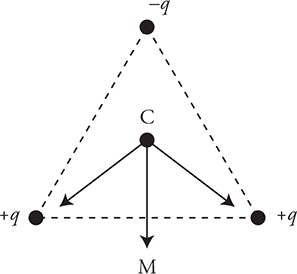
23. (A) See figure. Note: To get full credit, all the force vectors should be the same length. Two are diagonal toward the +q charges, and one is directly down and away from the —q charge.
(B) The force on the proton at M is less than the force on the electron at C. At point M, the forces from the two positive charges +q are equal and opposite and cancel out. In addition, the force from the negative charge —q is smaller in magnitude at point M than at point C.
24. (A) The electric fields at points N and P must be the same size. The electric field at O must be longer than the other two. See figure.
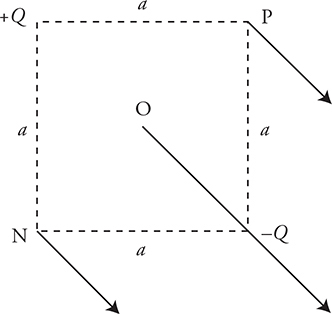
(B) Remember that electric potential is a scalar without direction. Simply sum up the individual potentials.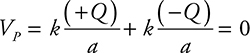 
. The electric potential will be zero at all three points because the charges are opposite in sign, and the radius is the same in each case.
(C) Work equals the negative change in electric potential energy. Since there is no change in electric potential moving from point P to point O, there is no change in the potential energy of the proton. Therefore, the work equals zero. In addition, the charge is moved perpendicular to the electric field; therefore, no work is done by the field.
(D) One way to accomplish this is to move —Q to point P. The electric fields from the two charges will combine to create a net E-field to the right. See figure.
25. (A) Charges 1 and 3 are positive. Charge 2 is negative. The electric field vectors point toward negative charges and away from positive charges.
(B) The force will be in the opposite direction of the electric field. See figure.
(C) The isolines should be perpendicular to the electric field vectors. See figure for an example of the sketch.
(D) The isoline through point A will be at a higher electric potential because it is closer to the positive charge. In addition, electric field lines point toward lower electric potential.
26. (A) The isolines closest to 1 are positive; therefore, 1 is positive. The isolines nearest 2 are more negative, so 2 is negative.
(B) i. Positive charges will naturally move toward more negative electric potential areas because the electric field will point in that direction. Therefore, the proton will end up 40 V lower in potential than it started; this will be the —20 V isoline.
ii. a. In the system that includes the two charges and the proton, the electric potential energy stored in the system decreases and converts to kinetic energy for the proton.
b. In the system that includes only the proton, the external electric field from the two charges does positive work on the proton, giving it kinetic energy.
(C) Decreased. ΔUE = qΔV the change in electric potential is positive but the charge is negative. This gives us a negative change in electric potential energy.
(D)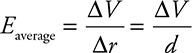 
. The electric field always points toward decreasing electric potential, which is to the right.
(E)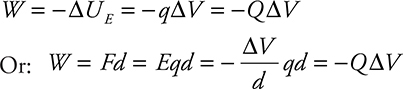 
(F) See the figure. The electric field vectors are always perpendicular to the isolines and point from more positive to less positive electric potential. The greater the change in electric potential in the area, the greater the electric field: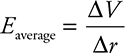 
. Therefore, the arrow at point C should be longer than the one at point A.
27. (A)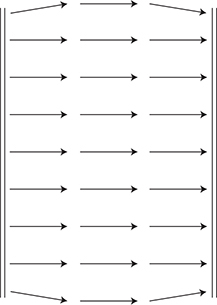 
(B) 
(C)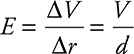 
(D) 
(E) The net charge is zero because the charge on the two plates are the same magnitude, but opposite in sign.
(F)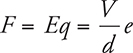 
. The gravitational force is usually much smaller than the electric force, and can be ignored in this case, because the magnitude of the proton mass is much smaller than the magnitude of the charge. The only time we need to worry about gravity is when the magnitude of the mass is much larger than the net charge of the object.
(G) Using Forces:
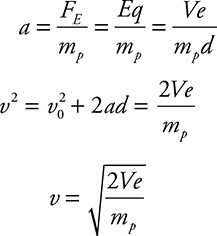
Using Energy:
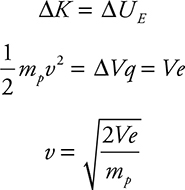
The answers you get by using forces and energy are the same. (As they should be!)
(H) The proton released from the center of the capacitor has a final velocity that is smaller than the proton released from the negative plate. Both have the same acceleration:
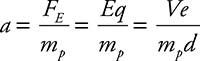
But, the one released from the middle of the capacitor has less distance to accelerate: 
.
Or, we can just say that the proton released from the middle of the capacitor moves through a smaller electric potential, thus reducing its final velocity: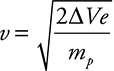 
.
28. (A) The two charges cancel each other out and the capacitance will remain the same:
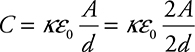
(B) The capacitance remains the same as it is determined by the geometry of the capacitor itself:
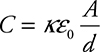
Since the capacitance stays the same, the charge on the plates will double: 
(C) Capacitance is directly proportional to the plate area. So the graph is a line with a positive slope. See figure.
(D) Capacitance is inversely proportional to the distance between the plates. Therefore, the graph will be a hyperbola. See figure.
(E) We need the most stored energy in order to light the bulb for the longest possible time: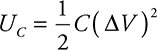 
. We need the largest capacitance possible: 
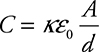. Therefore, we need the largest dielectric constant, largest plate area, and the smallest plate spacing we can get.
❯ Rapid Review
• Matter is made of protons, neutrons, and electrons. Protons are positively charged, neutrons have no charge, and electrons are negatively charged.
• Like charges repel; opposite charges attract.
• An induced charge can be created in an electrically neutral object by placing that object in an electric field.
• Objects can be permanently charged by contact, where the two objects touch and share the net charge.
• Objects can be charged by induction, where a charged object A is brought close to object B causing it to become polarized. An escape path is made such that the repelled charge is driven off of object B. Then the escape path is removed with the result that object B is permanently charged the opposite sign of A.
• When charge moves from object to object, the net charge of the system remains constant—conservation of charge.
• Charge is quantized, with the minimum size charge of an electron/proton: ±1.6 × 10—19 C.
• Protons are trapped on the nucleus. Electrons are easily moved from place to place.
• The electric force on an object depends on both the object’s charge and the electric field it is in.
• Unless stated otherwise, the zero of electric potential is at infinity.
• Equipotential lines show all the points where a charged object would have the same electric potential. Equipotential isolines are always perpendicular to electric field vectors.
• The electric field between two charged parallel plates is constant except near the edges. The electric field around a charged particle depends on the distance from the particle and points radially inward for negative charges and outward for positive charges.
• Electric forces and electric fields are vector quantities that must be added like any other vectors, using a free-body vector diagram.
• Charged objects obey Newton’s laws, conservation of energy, and conservation of momentum, and they can have accelerations, velocities, and displacements just as in mechanics.
• The electric field inside a charged conductor is zero and the electric potential inside is a constant. Any charge inside will not feel any electric force.