5 Steps to a 5: AP Physics 2: Algebra-Based 2024 - Jacobs Greg 2023
STEP 4 Review the Knowledge You Need to Score High
13 Magnetism and Electromagnetic Induction
IN THIS CHAPTER
Summary: Magnetic fields produce forces on moving charges; moving charges, such as current-carrying wires, can create magnetic fields. This chapter discusses the production and the effects of magnetic fields.

Key Ideas
![]() Magnetic poles always come in pairs (dipoles); you will never find a monopole (north or south by itself).
Magnetic poles always come in pairs (dipoles); you will never find a monopole (north or south by itself).
![]() Magnetic fields, just like electric fields, extend to infinity.
Magnetic fields, just like electric fields, extend to infinity.
![]() The study of magnetic behavior is inherently three-dimensional (3D) and we use “right-hand rules” to help us visualize its behavior.
The study of magnetic behavior is inherently three-dimensional (3D) and we use “right-hand rules” to help us visualize its behavior.
![]() The force on moving charges due to the magnetic field is qvB.
The force on moving charges due to the magnetic field is qvB.
![]() The direction of the magnetic force on a moving charge is given by a right-hand rule and is not in the direction of the magnetic field.
The direction of the magnetic force on a moving charge is given by a right-hand rule and is not in the direction of the magnetic field.
![]() The magnetic force is always perpendicular to the moving charges’ velocity. This causes a moving charge in magnetic field to arc into circular paths.
The magnetic force is always perpendicular to the moving charges’ velocity. This causes a moving charge in magnetic field to arc into circular paths.
![]() Current-carrying wires produce magnetic fields.
Current-carrying wires produce magnetic fields.
![]() When the magnetic flux through a wire loop changes, a voltage is induced.
When the magnetic flux through a wire loop changes, a voltage is induced.
![]() Materials placed in a magnetic field will exhibit one of three behaviors: ferromagnetism, paramagnetism, or diamagnetism.
Materials placed in a magnetic field will exhibit one of three behaviors: ferromagnetism, paramagnetism, or diamagnetism.
Relevant Equations
Magnetic Fields
Some people might think of a screwdriver that holds on to a screw or magnets on a refrigerator when they think of magnetism, or a horseshoe-shaped piece of metal doing amazing things in a cartoon. But physicists know that magnetism goes far beyond picking up a bunch of paper clips. Magnetism is different from any other subject you’ve learned before because much of magnetic behavior is three-dimensional. There are many right-hand rules that are indispensable to understanding magnetism, as well as concepts that are completely different from anything you’ve learned before. But hang in there; I’m going to help you get a pile of points on your magnetism questions on the AP exam.
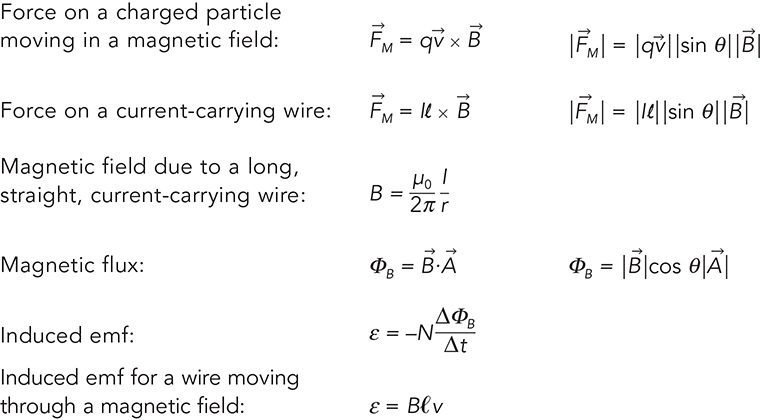
All magnets have north and south poles at their ends. There is no such thing as a monopole or single pole magnet.
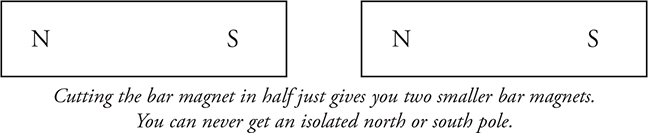
You can never create a monopole magnet with just a north pole or just a south pole. If you took the magnet in the next figure,

and cut it down the middle, you would not separate the poles. Instead, you would create two magnets like those shown in the following figure.
Be careful; do not confuse magnetism with static electricity. It’s an easy thing to do because there are some things that are very similar.
Similarities:
• Electric charges exert forces on each other. Opposite charges attract and like charges repel. Magnets exert forces on each other. Opposite poles attract and like poles repel.
• Charges produce electric fields that extend out into space to infinity and get weaker with distance. Magnets produce magnetic fields that extend out into space to infinity and get weaker with distance as well.
Huge Difference:
• Electric fields exert forces on positive charges in the direction of the field. Negative charges get pushed in the opposite direction of the electric field. Magnetic fields are not that simple. Magnetic fields affect only moving charges, and the force is perpendicular to both the velocity of the charge and the direction of the magnetic field!
But, we are getting ahead of ourselves. Let’s get back to magnetic fields. We will discuss all the unique behaviors of magnetism as we go along.
A magnet creates a magnetic field (see the next figure). Unlike electric field lines, which either emanate from a positive charge dead end on a negative charge, or extend infinitely into space, magnetic field lines always form loops. These loops extend infinitely into space. The loops point away from the north end of a magnet, and inward toward the south end. Near the magnet, the lines point nearly straight into or out of the poles.
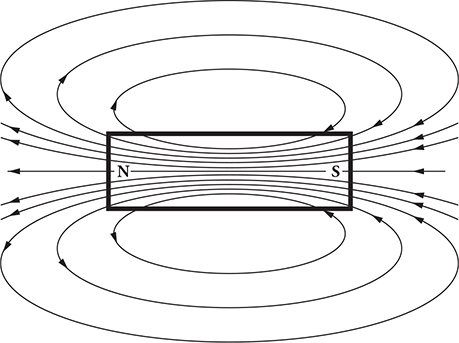
The figure below shows how iron filings sprinkled onto a bar magnet gather on the magnetic field lines, making them visible.

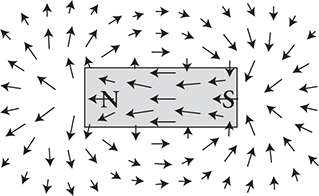
The next diagram shows the magnetic vector field representation. Each individual arrow represents the magnetic field vector at that point. Longer arrows mean a larger field strength.
The space around a magnet contains a magnetic field. All magnetic fields are created by moving charges. In a permanent magnet, like the ones you stick on your refrigerator, the moving charges are the electrons spinning around the nucleus of the atoms. Remember that currents are moving charges in a wire, so they also create magnetic fields. We will talk about that in a minute.
Remember that I said we would be dealing with three dimensions? A piece of paper is two-dimensional, so physicists came up with some nice ways to draw magnetic fields that are going in or out of the page. For a magnetic field going into the page, a bunch of X’s will be drawn. For a magnetic field coming out of the page, a bunch of dots will be drawn. In the next figure you will see two different variations of how each of these is drawn.
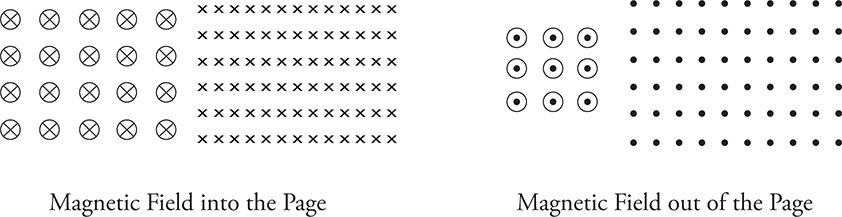
Magnetic Dipoles in a Magnetic Field
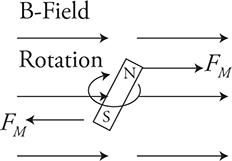
I hope you played with a compass as a kid. (If not, you probably have the app on your smartphone.) A compass is a tiny magnet mounted on a rotation point so that it can turn in the Earth’s magnetic field. It works like this: the north end of the magnet is forced in the direction of the magnetic field and the south end is forced in the opposite direction. This is just like the behavior of electric dipoles in an electric field. This is why a magnetic compass points north. Hey, wait a minute. Isn’t the north end of a magnet attracted to the south end of another magnet? Why yes, yes it is. That means that the geographic North Pole of the Earth is actually the magnetic south pole! (That’s why we can’t find Santa. His workshop is actually in Antarctica and the penguins are really elves. It all makes sense. . . .)
Magnetic Field Around a Straight Current-Carrying Wire
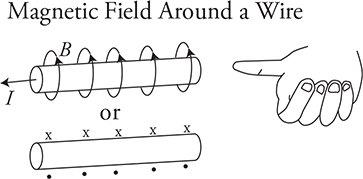
Maybe as a kid, you wrapped wire around a nail, connected it to a battery, and made an electromagnet. To start things out, we are going to keep things simple with a single straight piece of wire carrying a current. The magnetic field forms circles in the plane perpendicular to the wire. I know that sounds confusing, but picture a wire going through the center of a bunch of washers stacked one on top of the other. The washers are all circles in planes perpendicular to the wire. You are going to have to be able to find the direction of the magnetic field going around the wire, and we’re going to use something called the right-hand rule to help us out.
The right-hand rule will help us find the direction of the magnetic field by a long, straight, current-carrying wire. Call this the right-hand “curly fingers” rule. You’re going to use your pen or pencil to help out. Take your pencil and hold it in the direction the wire is oriented, with the tip pointing in the direction of the current. Next, grasp the pencil with your right hand and your thumb pointing in the direction of the current, the same direction the tip of your pencil is pointing. Your fingers will curl around the pencil in the same direction the magnetic field curls about the current.
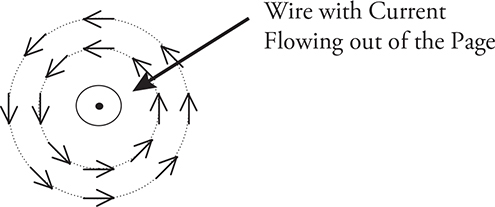
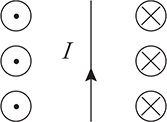
With the fingers of your right hand still holding the pencil, point the tip of the pencil directly at your face. See how your thumb points toward your eyes and your fingers circle around the pencil in a counterclockwise direction? When the current is directed upward, out of the page and toward your face, the magnetic field will form counterclockwise circles around the wire, as shown in the figure below.
Here’s another example. What does the magnetic field look like around a wire in the plane of the page with current directed upward toward the top of the page? We won’t walk you through this one; just use the right-hand rule, and you’ll be fine. The answer is shown in the next figure. (Notice how the magnetic field points into the page on the right-hand side of the current and out of the paper on the left-hand side of the current. Just like the fingers of your right-hand curl around the current when you point your right-hand thumb in the direction of the current.)
The formula to find the strength of a magnetic field outside a long straight wire is:
![]()
where:
• B is the magnetic field strength measured in teslas.
• μ0 is the vacuum permeability. (Don’t sweat it; μ0 is a constant. μ0 = 4π × 10—7 T · m/A.)
• I is the current going to the wire in amperes.
• r is the distance from the center of the wire to the point where you’re trying to find the magnetic field strength.
Question: What would the magnetic field look like in the space around a loop of wire with a counterclockwise current in it? Remember to use your right-hand rule!
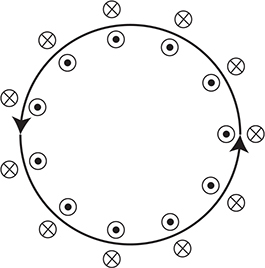
Answer: It would point out of the paper, in the middle of the loop, and into the paper on the outside of the loop.
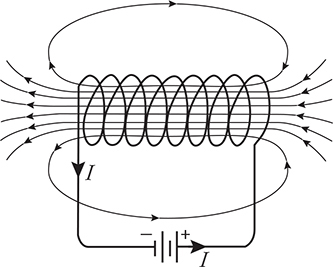
Now loop the wire around many times to create a coil called a solenoid. Hook it up to a battery and you get a dipole magnetic field that looks like a bar magnet, just like the one you got when you wrapped wire around that nail to produce an electromagnet as a kid. By the way, which end of the figure is the north end of the electromagnet? (Choose the left side!)
Force on a Moving Charged Particle
Whenever a charged particle passes through a magnetic field, if a component of its velocity is perpendicular to the magnetic field, it will experience a force. The magnitude of that force is:
![]()
Now you might be asking yourself, why is there a “×” between the velocity and the magnetic field strength? Well, you’re multiplying two vectors together, and that is called a “cross product.” Cross products act a little weirdly. First of all, the angle between the velocity vector and magnetic field vector has an effect on the magnitude of the force. If they’re at a right angle, you get a maximum force. If they’re parallel to each other, the force is zero. Another way of writing a cross product is:
![]()
where:
• ![]() is the force acting on the moving charge in Newtons.
is the force acting on the moving charge in Newtons.
• q is the charge of the particle moving to the field in coulombs.
• ![]() is the velocity of the particle in meters per second.
is the velocity of the particle in meters per second.
• ![]() is the magnetic field strength in teslas.
is the magnetic field strength in teslas.
• θ is the angle between the velocity and the magnetic field vectors.
Don’t worry too much about the cross-product equation. I know it’s on the reference table, but the equation with “sin θ” will serve you fine.
Here comes the really strange thing about a cross product: the force acting on the charge is at a right angle to both the magnetic field and the velocity. Of course, there is a hand rule to help you out. (If the right-hand rule that follows is not the one that your teacher taught you, don’t worry! There are several different variations of this right-hand rule. The point is for you to find one that works for you and stick with it.)
Here’s the right-hand rule for a moving positive charge in a magnetic field. (You might want to call this the right-hand “flat finger” rule.) Hold your hand flat with your thumb at a right angle to your fingers.
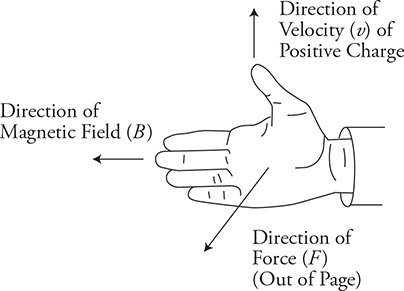
• Your fingers should point in the direction of the magnetic field. There are usually lots of magnetic field lines and you have lots of fingers.
• Your thumb will point in the direction of the velocity of the particle.
• Perpendicular to the palm of your hand is the direction of the force on the particle. A nice way to think of this is that the direction of the force on the particle is the same direction you would push on something with the palm of your hand.
Notice that everything is at right angles. If the velocity is not perpendicular to the magnetic field, you can bring your thumb a little closer or farther away (if you can) from your fingers. The force is always going to be perpendicular to the two of them and will be in the direction your palm is facing.
What if there is a negative particle moving through the field? Everything is reversed for the negative particle, so simply use your left hand and follow the same rules. So remember:
• Right hand for positive particles
• Left hand for negative particles
Now is a good time for “body art.” Take a pen and write a B on the tip of each of your fingers. Write v on your thumb and put a big F and a positive sign “+” on your right palm. Repeat this for your left hand except put a big F and a negative sign “−” on your left palm. Now you have a useful physics tattoo to help you with these problems. (Remember, you can’t walk into the AP exam with anything written on your hands. But once the exam starts, you can tattoo yourself if you need to!)
The key to this right-hand rule is to remember the sign of your particle. This next problem illustrates how important the sign can be.
An electron travels through a magnetic field, as shown below. The particle’s initial velocity is 5 × 106 m/s, and the magnitude of the magnetic field is 0.4 T. What are the magnitude and direction of the particle’s acceleration?
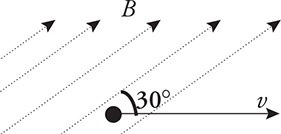
This is one of those problems where you’re told that the particle is not moving perpendicular to the magnetic field. So the formula we use to find the magnitude of the force acting on the particle is
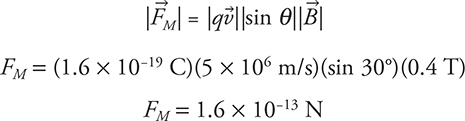
Note that we never plug in the negative signs when calculating force. The negative charge on an electron will influence the direction of the force, which we will determine in a moment. Now we solve for acceleration:
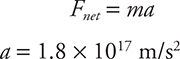
Wow, you say . . . a bigger acceleration than anything we’ve ever dealt with. Is this unreasonable? After all, in less than a second the particle would be moving faster than the speed of light, right? The answer is still reasonable. In this case, the acceleration is perpendicular to the velocity. This means the acceleration is centripetal, which means the force is toward the center and the particle must move in a circle at constant speed. But even if the particle were speeding up at this rate, either the acceleration wouldn’t act for very long, or relativistic effects would prevent the particle from traveling faster than light.
Now that you found the magnitude of the force, you want to find the direction. Be careful; it’s an electron, so you need to use your left hand. To do this you’re going to hold your left hand with your fingers pointing in the direction of the magnetic field and your thumb pointing in the direction of the velocity. Notice this leaves your palm pointing straight into the page, so the force acting on the particle is directly into the page. Some questions will tell you that toward the right of the page is the positive x-axis, the top of the page is the positive y-axis, and directly out a page, toward your face, is the positive z-axis. So this force would be in the negative z direction (—z).
Quick question: If the electron in the previous problem was traveling parallel to the magnetic field, what would happen? Nothing. The angle θ between the field and the velocity would be 0°, or maybe 180°. In either case the sin 0° = sin 180° = 0. Since the magnetic force is zero, the electron would just keep moving like the magnetic field wasn’t even there. Can you hear Newton’s ghost saying, “An object in motion stays in motion unless acted upon by a net outside force”?
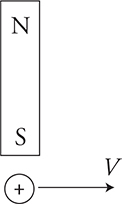
Another quick question: A positive charge, moving to the right, passes the south end of a magnet. What is the direction of the force on the magnet? That’s not a typo. What is the force on the magnet? Remember Newton’s third law—for every force there is another one that acts in the opposite direction on the other object. Just figure out the direction of the force on the charge and the force on the magnet will be in the opposite direction. We already know that magnetic fields enter the south end of the magnet, which means upward on the paper. Velocity is to the right. Charge is positive—use your right tattooed hand to find the force on the charge will be out of the paper. Therefore, the force on the south end of magnet will be into the paper.
Magnetic Force on a Wire
Before we get into this, let’s first think about two bar magnets side by side. See the diagram below. If the two magnets have opposite poles near each other, they’re going to attract each other, and if they have like poles near each other, they’re going to repel each other. But let’s think about how the magnetic fields interact.
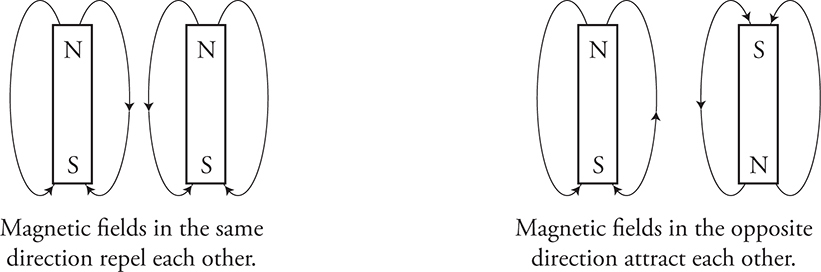
Keep this in mind as we think about a wire in a magnetic field. Looking at the next figure, there’s a wire with current coming out of the page sitting in a magnetic field going toward the right side of the page. The magnetic field around the wire is going counterclockwise as indicated by our right hand “curly fingers” rule. Above the wire the magnetic field from the wire is in the opposite direction of the magnetic field from the outside magnets, so those magnetic fields cause attraction pulling the wire up and pushing the magnets down. Below the wire, the magnetic fields are in the same direction, so they repel each other pushing the wire up and the magnets down. So both of these interactions are trying to push the wire up toward the top of the page.
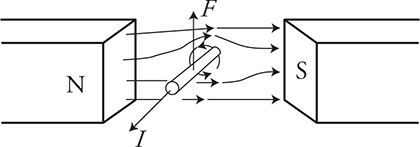
What’s nice about this is that we can use the same hand rule we just used. Remember, we consider current to be a positive charge flow, so for a current-carrying wire, we will always be using our right hand, never the left hand.
To use the right-hand rule for a current-carrying wire in a magnetic field, once again, you are going to hold your hand flat with your thumb perpendicular to your fingers:
• Your fingers point in the direction of the external magnetic field (to the right).
• Your thumb points in the direction of the current flowing in the wire (out of the page).
• Your palm aims in the direction of the force (upward toward the top of the page).
Practice this with the diagram above and prove that it works.
The equation for force on a current-carrying wire in a magnetic field is:
![]()
This is a cross product just like before, so we can write it like this:
![]()
where:
• ![]() is the force acting on the wire in newtons.
is the force acting on the wire in newtons.
• I is the current going to the wire in amperes.
• ℓ is the length of the wire.
• ![]() is the magnetic field strength in teslas.
is the magnetic field strength in teslas.
• θ is the angle between the current and the magnetic field.
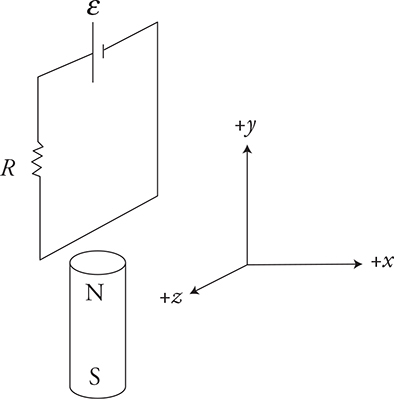
Question: The lower part of a circuit sits just above a magnet as shown in the diagram above. In what direction does the bottom wire of the circuit receive a force?
Answer: The north end of the magnet will produce a magnetic field upward in the +y direction. The battery produces a current that is counterclockwise or in the −z direction for the bottom wire. Using our right-hand “flat fingers” rule, we see that the force is in the +x direction.
Force Between Two Parallel Wires
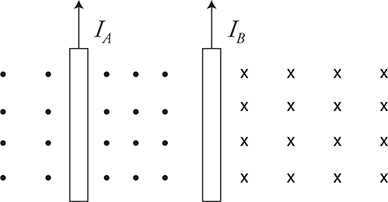
Finding the force between two parallel wires is easier than you would think. Just find the magnetic field around one wire and see how it affects the other wire. Let’s start with wire B in the figure above. What will the magnetic field look like surrounding the B wire? Using our right-hand “curly fingers” rule, we find that the magnetic field will point into the paper on the right of the wire and out of the paper on the left of the wire as seen in the figure. Notice that wire A is located in the magnetic field pointing out of the paper. So, just use the right-hand “flat fingers” rule to find that the force on the left wire will be to the right. What happens to wire B? What would Newton say? Newton’s third law says the force on wire B will be exactly the same size and to the left.
Finding the magnitude of the force is a little trickier but not bad. Remember that wire A is sitting in the magnetic field caused by wire B. If the wires are a distance r apart from each other, the strength of the magnetic field from wire B is:
![]()
The force on wire A caused by it sitting in the magnetic field from wire B is:
![]()
Since the current and the magnetic fields are at the right angle, θ = 1, we can drop it out. Combining the two equations, we get:
![]()
Of course, action/reaction still applies, so whatever force wire A experiences, wire B gets the same force, but in the opposite direction.
Charges in a Magnetic Field and the Mass Spectrometer
We have learned that magnetic forces are directed perpendicular to the velocity vector of the charge. Does that sound vaguely familiar to something you learned last year in AP Physics 1? Like the gravitational force from the Sun acting perpendicular to the velocity of Earth causing the Earth to move in a circular orbit?
Since the magnetic force is always perpendicular to the velocity of the charge, it does no work on the charge. It only changes its direction and gives the charge a centripetal acceleration. The force causes the direction of the charge’s velocity to change, but not its magnitude. So we get a nice circular path.
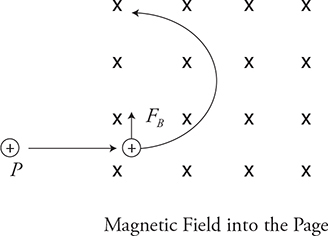
The image above shows a positive charge entering a magnetic field directed into the page. The magnetic force is always perpendicular to the velocity, causing the charge to move in a circular path.
You could be asked to find the radius of the path or the diameter of the circle. The magnetic force on the charge acts as a centripetal force:
Don’t worry about θ in this example because the velocity and magnetic fields are at a right angle to each other:
![]()
Notice how the radius depends on the momentum (mv) of the particle. Higher momentum = larger radius. The radius of the path is inversely related to the charge of the particle and the magnetic field strength. A larger charge and/or larger magnetic field give us a smaller radius. This equation for the radius of a charged particle’s path moving through a magnetic field is not on the official equation sheet you will receive. Make sure you know how to derive it!
If the particle enters the magnetic field at an angle with part of the velocity parallel to the field, the charge will take a helical path. (A helical path is like a stretched out Slinky. See the diagram above.) Remember that velocities parallel to the field do not create magnetic forces. Only velocities perpendicular to the field create a force. This is what causes Earth’s northern and southern lights. Charged particles from space hit the Earth’s magnetic field at an angle and helix along the field lines until they enter the atmosphere near the North and South Poles.
A device called a mass spectrometer uses arcing charges in a magnetic field to determine the charge-to-mass ratio q/m of an unknown particle by measuring the radius of the path the particle takes in the magnetic field.
Example
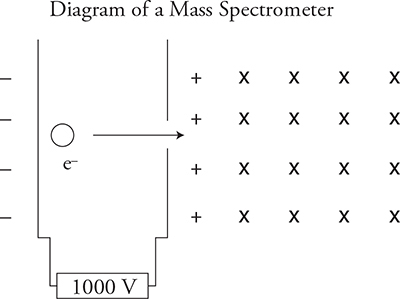
An electron is accelerated between two plates with the potential difference of 1000 V. It passes through a hole in one of the plates and enters a magnetic field of 0.1 T directed into the page. Find the radius of the path the electron makes in the magnetic field.
Looking at the figure above, we know that the electric field between the plates goes toward the left, but electrons experience a force in the opposite direction of the field. Therefore, the electron is accelerated toward the right. To find the speed of the electron as it enters the magnetic field, you can use conservation of energy:
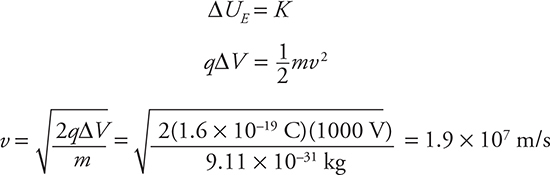
Now that the speed has been found, it’s easy to find the radius:
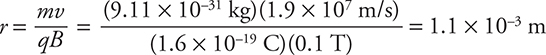
Which direction will the electron be curving? Remember to use the left-hand rule for negative charges. (The electron will curve downward toward the bottom of the page in a circular arc.)
What happens to the electron if it leaves the magnetic field? Remember Newton’s first law. (The electron will travel off in a straight line along the final direction it had when it leaves the magnetic field.)
Practice sketching several possible paths of the figure above because the AP exam likes to ask conceptual questions like this. If you find that your sketch looks “bad,” just write a note to the exam reader. Something simple and to the point like: “The path in the field is circular. Once it leaves the field it will travel in a straight line.” That is all you need to do! Remember that this is not an art exam. The exam readers are looking for your physics understanding, and a quick explanation will secure you points.
Particles Moving Through Both Magnetic and Electric Fields
Let’s review the differences between electric and magnetic fields. Look at the four fields in the next figure.
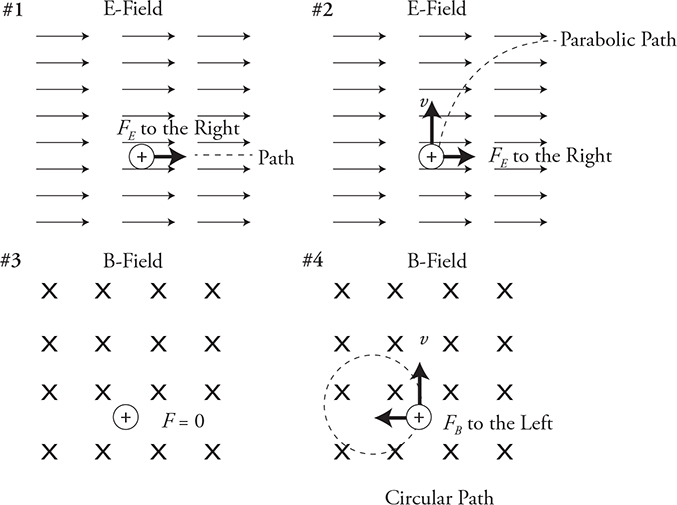
• Electric Fields: A positive charge in an electric field receives a force to the right. It does not matter if the particle is moving or not. Starting at rest (see #1), the particle will accelerate to the right. Starting with a velocity upward (see #2), the particle receives a force to the right and will travel along a parabolic path just like a baseball in Earth’s gravitational field.
• Magnetic Fields: A positive charge will not experience a force unless it is moving (see #3). Starting with a velocity upward (see #4), the particle will experience a centripetal force that causes it to arc into a circular path.
• Remember: If the charge is negative, the forces will be reversed in direction.
Make sure you keep these two different behaviors in mind because the AP exam likes to test you on them. For example: A proton is moving at 5 × 104 m/s toward the right between two charged parallel plates. The electric field between the plates is 2 × 105 N/C. Find the magnitude and direction of the magnetic field between the plates needed so the electron will continue in a straight line.
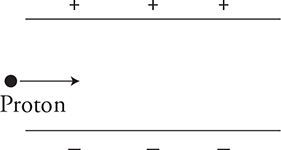
Let’s first work out the direction of the electric field. You know that the electric field between the plates points in the direction from high to low electric potential. Since the upper plate is positive and the lower plate is negative, the electric field is toward the bottom of the page. The proton is positive so it experiences an electric force toward the bottom of the page. But remember, we want the proton to move in a straight line, which means the force from the magnetic field has to balance out the force from the electric field and point toward the top of the page. Now it’s time to break out our right-hand “flat finger” rule. The magnetic force must be toward the top of the page so your palm needs to point toward the top of the page. The velocity is toward the right side of the page, so your thumb will point toward the right. If you set your hand up correctly, your fingers will point into the page, telling you that the magnetic field is aimed into the page.
We’ve already mentioned that the forces from the magnetic and electric fields must cancel each other out:
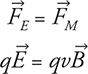
What’s nice is that the charge drops out, and since the velocity and magnetic field are at right angles to each other, we don’t need any trigonometry functions:
Magnetic Flux
Magnetic flux is a measure of the total magnetic field passing through an area. It is measured in webers. The connection between magnetic field strength (which is sometimes called magnetic flux density) and magnetic flux can be thought of like this: picture a square area 2 meters on each side with a total magnetic flux of 16 webers passing through that area. You can draw that with 16 X’s inside of that area, as shown in the next figure.

To find the field strength, all you have to do is divide the flux by the area:
![]()
The equation for magnetic flux is:
![]()
Notice the “dot” in the equation. This is called a dot product. When using a dot product, you are multiplying the magnitudes of the vectors and ending up with a scalar answer. Another way we can look at a dot product is:
![]()
Notice that we are using cosine. How can this relationship be applied? Picture a magnetic field going toward the right. You are holding a piece of paper in front of you with the magnetic field passing through the paper. As you turn the paper, at one point there is the most flux possible passing through the paper. (See the left side of the following figure.) If the paper is then turned 90°, none of the magnetic flux will pass through the piece of paper. (See the right side of the figure.)
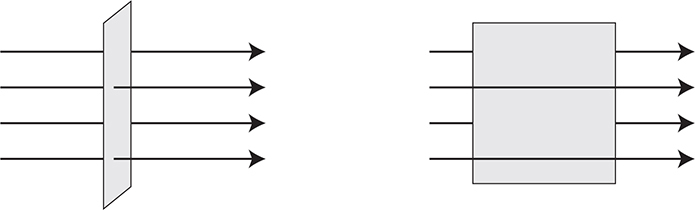
Just remember: There’s maximum flux when the field passes directly through the area and no flux when the field passes by, but not through, the area.
Electromagnetic Induction
Of all the technological innovations that have been implemented, generating electricity may be the most useful. Most people don’t really have any idea how the majority of our electricity is actually generated, but you, as an AP Physics ace, do. So let’s take this step by step.
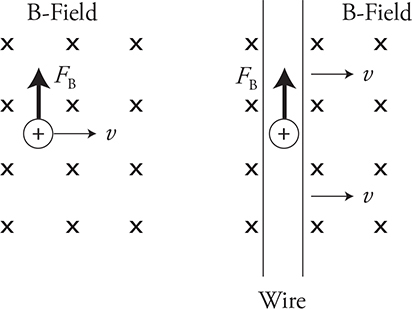
To understand how electromagnetic induction works, picture a proton moving toward the right in a magnetic field aiming into the page. Using the right-hand rule, the force acting on the proton will be toward the top of the page. Now let’s take a look at a wire being dragged toward the right as shown in the second image. Conventional current is considered to be the flow of positive charge, so if you picture a positive charge in that wire, it will get a force toward the top of the page as the wire is moved to the right. In fact, every positive charge in the wire will get that force, which will produce a current moving toward the top of the wire.
This is called an electromotive force, emf, or ε, measured in volts. To find the electromotive force, or emf, of a wire moving through a magnetic field:
![]()
where:
• ε is the electromotive force in volts.
• B is the magnetic field strength in teslas.
• ℓ is the length of the wire embedded within the magnetic field in meters.
• v is the velocity of the wire in meters per second.
Another way we can use electromagnetic induction to produce currents is to have a loop of wire that has a changing magnetic field through the inside of that loop. This can be done by:
• Changing the magnetic field strength
• Changing the flux area of the loop
• Changing the direction the loop is facing in the field (Turning the loop so it’s parallel to the field and then turning it so that it’s perpendicular to the field will change the amount of magnetic flux in the loop.)
To find the emf:
![]()
where:
• N is the number of wraps of wire in the loop.
Remember that an emf is like a battery. That means, if you have a loop of wire in a magnetic field, all you have to do is change one of these three things:
1. magnetic field strength
2. size of the flux area
3. orientation of the loop in relation to the magnetic field
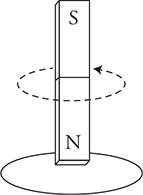
and you get an emf that will produce electric current! The electric company uses option #3. They rotate huge coils of wire and enormous magnets past each other to induce current and send it down power lines to your house along with a monthly electric bill.
Let’s take a closer look at the details of inducing an emf.
Up until now, we’ve just said that a changing magnetic flux creates a current. We haven’t yet told you, though, in which direction that current flows. To do this, we’ll turn to Lenz’s law.
Lenz’s law: States that the direction of the induced current opposes any change in flux.
When a current flows through a loop, that current creates its own magnetic field. So what Lenz said is that the current that is induced will flow in such a way that the magnetic field it creates points opposite to the direction in which the already existing magnetic flux is changing.
Sound confusing?1 It’ll help if we draw some good illustrations. So here is Lenz’s law in pictures.
We’ll start with a loop of wire that is next to a region containing a magnetic field. Initially, the magnetic flux through the loop is zero.
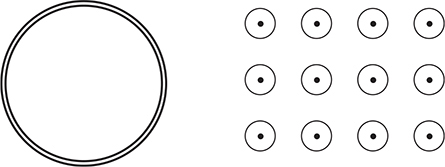
Now, we will move the wire into the magnetic field. When we move the loop toward the right, the magnetic flux will increase as more and more field lines begin to pass through the loop. The magnetic flux is increasing out of the page—at first, there was no flux out of the page, but now there is some flux out of the page. Lenz’s law says that the induced current will create a magnetic field that opposes this increase in flux. So the induced current will create a magnetic field into the page to oppose the increasing flux out of the page. By the right-hand rule, the current will flow clockwise. This situation is shown in the next illustration.

After a while, the loop will be entirely in the region containing the magnetic field. Once it enters this region, there will no longer be a changing flux, because no matter where it is within the region, the same number of field lines will always be passing through the loop. Without a changing flux, there will be no induced emf, so the current will stop. This is shown in the next illustration.
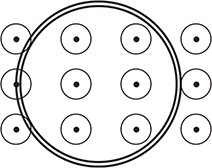
To solve a problem that involves Lenz’s law, use this method:
• Point your right thumb in the initial direction of the magnetic field.
• Ask yourself, “Is the flux increasing or decreasing?”
• If the flux is decreasing, Lenz says we need to cancel out this decrease in flux by adding magnetic field in the direction your thumb is pointing. Just curl your fingers (with your thumb still pointed in the direction of the magnetic field). Your fingers show the direction of the induced current.
• If flux is increasing in the direction you’re pointing, then Lenz says we need to cancel this increase. So, point your thumb in the opposite direction of the magnetic field, and curl your fingers. Your fingers show the direction of the induced current.
Induced emf in a Rectangular Wire
Consider the example in the earlier figures with the circular wire being pulled through the uniform magnetic field. It can be shown that if instead we pull a rectangular wire into or out of a uniform field B at constant speed v, then the induced emf in the wire is found by
![]()
Here, ℓ represents the length of the side of the rectangle that is cutting through the magnetic field lines, as shown below.
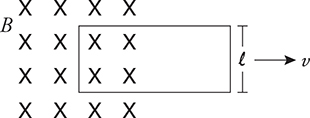
Notice how the rectangle is being pulled from the field. That means the magnetic flux is decreasing. Using Lenz’s law rules, we find that the induced current in the rectangle of wire will be clockwise.
We use electromagnetic induction:
• to generate electricity
• in microphones to turn our voices into electrical currents and then convert those currents back into sound with speakers
• to run motors
• in MRIs and other medical devices
• on those magnetic strips on the back of credit cards
• and the list goes on and on
It is truly a powerful tool.
Magnetic Behavior of Materials
You may have noticed not every material seems to react to a magnet. There are actually three types of magnetic behavior that materials exhibit.
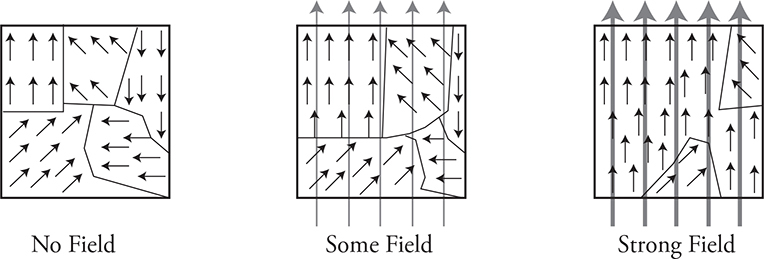
1. Ferromagnetism: Materials like iron, nickel, and cobalt have multiple unpaired electrons that tend to create localized regions of magnetic fields inside the material called domains. When these materials are placed in an external magnetic field, the domains align with the external magnetic field, amplifying it many times. In a strong enough external field, the domains can grow and merge, creating a permanent magnet. (See the figure above.) This is why a current-carrying wire wrapped around an iron nail will produce such a strong magnet. Ferromagnetic materials are strongly attracted by magnets.
2. Paramagnetism: The magnetic properties of the material tend to align with an external magnetic field, but the result is weak and does not enhance the magnetic field very much. These materials will not produce a permanent magnet. Paramagnetic materials are very weakly attracted to magnets.
3. Diamagnetism: When placed in a magnetic field, the internal magnetic properties of the material align opposite to the external field, cancelling out part of the field. Water and graphite behave this way. Diamagnetic materials are very weakly repelled by magnets.
❯ Practice Problems
Multiple Choice
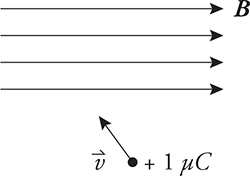
1. A point charge of +1 μC moves with velocity v into a uniform magnetic field B directed to the right, as shown above. What is the direction of the magnetic force on the charge?
(A) to the right and up the page
(B) directly out of the page
(C) directly into the page
(D) to the right and into the page
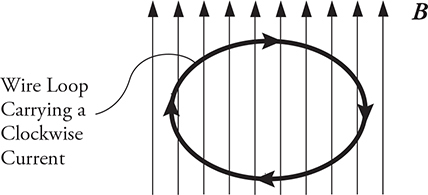
2. A uniform magnetic field B points up the page, as shown above. A loop of wire carrying a clockwise current is placed at rest in this field, as shown above, and then let go. Which of the following describes the motion of the wire immediately after it is let go?
(A) The wire will expand slightly in all directions.
(B) The wire will contract slightly in all directions.
(C) The wire will rotate, with the top part coming out of the page, and the bottom part going into the page.
(D) The wire will rotate, with the left part coming out of the page, and the right part going into the page.
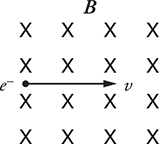
3. An electron moves to the right in a uniform magnetic field that points into the page. What is the direction of the electric field that could be used to cause the electron to travel in a straight line?
(A) down toward the bottom of the page
(B) up toward the top of the page
(C) into the page
(D) out of the page
4. The vector force field surrounding a bar magnet has a shape similar to the force field surrounding which of the following?
(A) two stars of the same mass in a binary star system
(B) a proton and electron in a hydrogen atom
(C) two equally charged Van de Graaff generators placed close to each other on a lab table
(D) an alpha particle
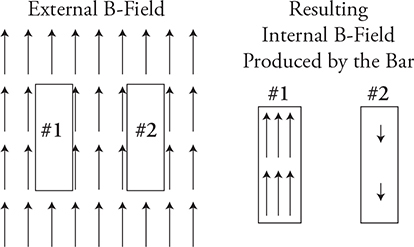
5. Two bars of differing materials are placed in an external magnetic field as shown above. The resulting internal magnetic field in each bar is depicted in the second figure. Which of the following correctly describes the two materials?
(A) Bar 1 is a ferromagnetic material; bar 2 is a paramagnetic material.
(B) Bar 1 is a ferromagnetic material; bar 2 is a diamagnetic material.
(C) Bar 1 is a non-magnetic material; bar 2 is a paramagnetic material.
(D) Bar 1 is a non-magnetic material; bar 2 is a diamagnetic material.

6. A scientist sends two identical negative charges —q moving to the right. One is in a magnetic field and one is in an electric field as shown in the figures above. The scientist observes the motion of both charges. Which of the following correctly indicates the direction each charge will turn?

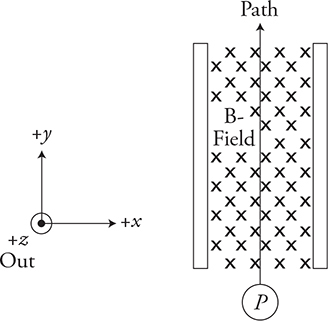
7. A magnetic field directed into the page in the −z direction is placed between the plates of a charged capacitor as shown in the figure. The magnetic and electric fields are adjusted so that a particle (P) of charge +1e moving at a velocity of v will pass straight through the fields in the +y direction. Which direction is the electric field in the region between the plates?
(A) +x direction
(B) −x direction
(C) +z direction
(D) −z direction

8. A small magnet is placed in a uniform magnetic field that is pointing up out of the paper in the +z direction. If the magnet is free to move in the field, which of the following is a correct statement about its motion?
(A) There is a torque that rotates the magnet about the y-axis.
(B) There is a torque that rotates the magnet about the z-axis.
(C) There is a force that moves the magnet along the z-axis.
(D) The forces on the magnet cancel and the magnet will not move.
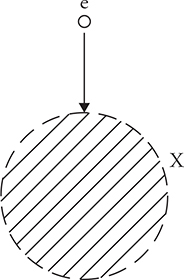
9. An electron is moving downward toward the bottom of the page when it passes through a region of magnetic field, as shown in the figure above by the shaded area. The electron travels along a path that takes it through the spot marked X. The gravitational force on the electron is very small. What is the direction of the magnetic field?
(A) Toward the bottom of the page
(B) Toward the top of the page
(C) Out of the page
(D) Into the page
Questions 10—11
A proton is moving at a velocity of 6.0 × 104 m/s to the right, in the plane of the page, when it encounters a region of magnetic field with a magnitude 0.12 T perpendicular to the page, as shown in the figure below.
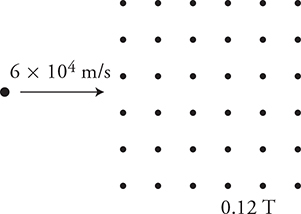
10. Which of the following is the radius of curvature of the path of the proton?
(A) 5 × 101 m
(B) 5 × 10-3 m
(C) 5 × 10-5 m
(D) 5 × 10-7 m
11. The proton is replaced with an electron moving in the same direction and at the same speed. Which of the following best describes the deflection direction and the radius of curvature of the electron in the magnetic field?

Questions 12—13
An electron is traveling at a constant speed of v parallel to a wire carrying a current of I, as shown in the figure below. The electron is a distance of d from the wire.

12. Which of the following is true concerning the force on the current-carrying wire due to the electron?
(A) The force is directed toward the right.
(B) The force is directed toward the left.
(C) The force is directed into the page.
(D) There is no force on the current-carrying wire due to the electron.
13. The force on the electron from the current is F. Which of the following will increase the force to 2F? (Select two answers.)
(A) Halve the distance of the electron to the wire.
(B) Halve the velocity of the electron.
(C) Double the current in the wire.
(D) Double the current in the wire and halve the distance of the electron to the wire.
Free Response
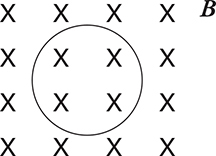
14. A loop of wire is located inside a uniform magnetic field, as shown above. Name at least four things you could do to induce a current in the loop.
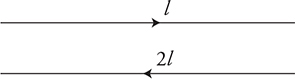
15. Two long wires, a distance (d) apart, carry different currents in opposite directions, as shown in the figure above. The bottom wire has a current twice that of the top wire.
(A) What is the direction of the magnetic force on the top wire?
(B) How does the magnetic force on the bottom wire compare in strength and direction to the force on the top wire? Justify your claim.
(C) Which way is the net magnetic field directed at the midpoint between the wires? Explain your reasoning.
(D) Derive an algebraic expression for the force per unit length on the top wire by the lower wire.

16. A particle is moving toward a magnetic field directed into the page, as shown in the figure above. Sketch and label the path taken by each of the following particles. Draw all of the pathways in proportion to the paths taken by all other particles. All particles enter the magnetic field with the same initial velocity and direction.
(A) Neutron
(B) Proton
(C) Electron
(D) Positron
(E) Alpha particle
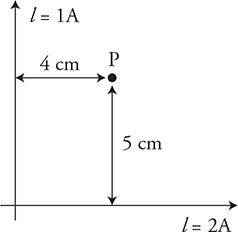
17. Two perpendicular wires carry currents of 1.0 A and 2.0 A, as shown in the figure above. Point P is 4 cm from the 1.0 A wire and 5 cm from the 2.0 A wire. Show all your work.
(A) Calculate the net magnitude and direction of the magnetic field at point P.
(B) Calculate the magnitude and direction of the force on a proton placed at point P.
(C) Calculate the magnitude and direction of a force on an electron at point P, moving at 3.5 × 106 m/s toward the right.

18. A proton traveling toward the top of the page at a velocity of v passes by a magnet, as shown in the figure above.
(A) What is the direction of the force on the proton?
(B) What is the direction of the force on the magnet? Explain your answer.
(C) What happens to the force on the proton if the velocity is doubled to 2v?
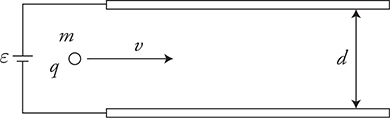
19. A positively charged particle (q) of mass m travels horizontally, with a velocity of v, through the center of two capacitor plates. The plates are separated by a distance of d and connected to a battery of potential difference (ε), as shown in the figure above.
(A) Sketch the electric field between the plates.
(B) Derive an algebraic expression for the electric field between the plates in terms of given quantities. Show all your work.
(C) Describe the motion of the particle as it passes through the capacitor plates. What shape is the path? Which direction is the acceleration? Explain your reasoning.
(D) What direction of magnetic field is needed to make the particle travel horizontally straight through the capacitor plates? Justify your answer.
(E) Derive an algebraic expression for the magnitude of the magnetic field needed to cause this straight, horizontal motion between the plates in terms of given quantities. Show all your work.
(F) The crossed electric and magnetic fields are adjusted to cause positively charged particles with a velocity of v to travel straight. What happens to a particle traveling at 2v? Will it travel straight, or will it curve? Justify your answer.
(G) The crossed electric and magnetic fields are tuned to cause positively charged particles with a velocity of v to travel straight. What happens to a negatively charged particle traveling at v? Will it travel straight, or will it curve? Justify your answer.
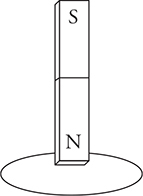
20. A loop of wire is positioned perpendicular to the end of a magnet, as shown in the figure above.
(A) Describe at least two ways to move the wire loop that will produce current in the wire. Explain why each method produces current.
(B) Describe at least two ways to move the magnet so current is produced in the wire. Explain why each method produces current.
(C) Describe at least two methods of how the magnet and/or wire loop can be moved that will not produce current. Explain why neither of these methods produce current.
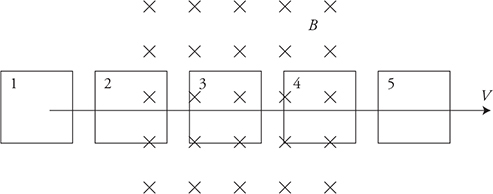
21. A rectangular loop of wire travels to the right and passes through a region of magnetic field into the page, as shown in the figure above.
(A) At which locations will current be induced in the wire? Explain your answer.
(B) At the locations where current is induced, what direction is the current in the wire loop—clockwise or counterclockwise? Explain your answer.
❯ Solutions to Practice Problems
1. (C) Use the right-hand rule for the force on charged particles. You point your thumb in the direction of the velocity, and point your fingers in the direction of the magnetic field. This should get your palm facing into the page. Because this is a positive charge, no need to switch the direction of the force.
2. (C) Use the right-hand rule for the force on a wire. Look at each part of this wire. At the leftmost and rightmost points, the current is along the magnetic field lines. Thus, these parts of the wire experience no force. The topmost part of the wire experiences a force out of the page (point your thumb to the right, fingers point up the page, the palm points out of the page). The bottommost part of the wire experiences a force into the page. So, the wire will rotate.
3. (A) Use the right-hand rule for the force on a charge. Point your thumb in the direction of velocity, point your fingers into the page, your palm points up the page . . . but this is a negative charge, so the force on the charge is down the page. (Or, you could have used the “left-hand rule” for negative charges!) Now, the electric force must cancel the magnetic force for the charge to move in a straight line, so the electric force should be up the page. (E and B fields cannot cancel, but forces sure can.) The direction of an electric force on a negative charge is opposite the field; so the field should point down, toward the bottom of the page.
4. (B) The two opposite poles of a magnet will have similar field characteristics to the two opposite sign charges in a hydrogen atom.
5. (B) When placed in an external magnetic field, magnetic domains inside a ferromagnetic material will strongly align with the external field, which intensifies the strength of the field. Diamagnetic materials, on the other hand, will generate an internal magnetic field in the opposite direction, weakening the strength of the field.
6. (C) Using the right-hand rule (or left-hand rule!) for moving charges in a magnetic field, the negative charge receives a force toward the bottom of the page. (Remember that this is a negative charge!) Electric forces are always parallel to the field, but opposite in direction for negative charges.
7. (A) Using the right-hand rule for magnetic forces on moving charges, we see that the magnetic force will be directed to the left. Therefore, we need an electric force to the right. Since the particle is positively charged, we need an electric field to the right to accomplish this.
8. (A) The north pole receives a force out of the page, and the south pole receives a force in the opposite direction into the page. This will create a torque on the magnet, rotating it about the y-axis.
9. (C) The original velocity of the electron is toward the bottom of the page. The force on the electron is to the right. Therefore, by the right-hand rule, the magnetic field is out of the page. Remember that the electron is negative and receives a force opposite to what positive receives!
10. (B) 
11. (D) 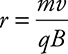 . The mass of the electron is smaller; therefore, the radius is smaller as well. The charge is opposite, so the electric force is in the opposite direction.
. The mass of the electron is smaller; therefore, the radius is smaller as well. The charge is opposite, so the electric force is in the opposite direction.
12. (A) The magnetic field, due to the current in the wire near the electron, is into the page. By the right-hand rule, the negative electron will receive a force to the left due to the current. By Newton’s third law, the force on the wire will be equal and opposite to the right.
13. (A) and (C) Combining the magnetic force on a moving charge equation with the magnetic field around a wire equation we get: 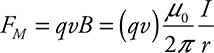 . From this we can see that cutting the distance in half or doubling the current will cause the force to increase by a factor of two.
. From this we can see that cutting the distance in half or doubling the current will cause the force to increase by a factor of two.
14. The question might as well be restated, “name four things you could do to change the flux through the loop,” because only a changing magnetic flux induces an emf.
(A) Rotate the wire about an axis in the plane of the page. This will change the θ term in the expression for magnetic flux, BA cos θ.
(B) Pull the wire out of the field. This will change the area term, because the magnetic field lines will intersect a smaller area of the loop.
(C) Shrink or expand the loop. This also changes the area term in the equation for magnetic flux.
(D) Increase or decrease the strength of the magnetic field. This changes the B term in the flux equation.
15. (A) The bottom wire produces a magnetic field into the page, in the region of the top wire, which causes a force directed upward toward the top of the page and away from the lower wire.
(B) According to Newton’s third law, the force is equal in strength but opposite in direction.
(C) Using the right-hand rule for wires we see that the magnetic field produces by the top wire points into the page between the wires. The magnetic field from the bottom wire also points into the page between the wires. Therefore, the net field is into the page.
(D) The magnetic force on the top current-carrying wire is due to the magnetic field of the lower wire:
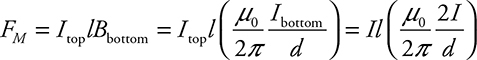
Therefore, the force per unit length of wire is 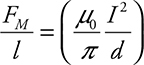 .
.
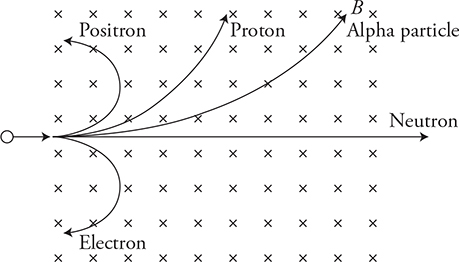
16. Note that the neutron travels along a straight path. All positive particles curve toward the top of the page. The proton, electron, and positron all have the same charge, velocity, and magnetic force acting on them. Therefore, the lightest particles will curve with a tighter radius. The positron and electron have the same radius of curvature. The alpha particle has twice the charge of the proton, which means it will receive twice the force. However, it is also four times the mass of the proton. Therefore, it will have a greater momentum per magnetic force and will curve less.
17. (A) Using the right-hand rule for magnetic fields produced around wires we see that the fields are in opposite directions at point P. Remember to convert your distance to meters.
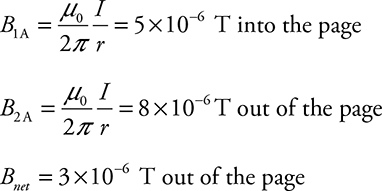
(B) The force is zero because the proton is not moving!
(C) ![]() toward the top of the page.
toward the top of the page.
18. (A) The magnetic field is to the left. By the right-hand rule, the force is out of the page.
(B) Into the page, by Newton’s third law.
(C) The force is proportional to the velocity; therefore, the force is doubled. The direction is the same.

19. (A) The field should be uniform and constant, filling all the space between the plates. Due to the polarity of the battery, the top plate is positive. Therefore, the electric field is directed downward.
(B) 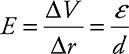
(C) The particle will accelerate downward toward the bottom plate in a parabolic path.
(D) We need a magnetic force upward to cancel the electric force downward on the positively charged particle. Using the right-hand rule, the magnetic field must point into the page.
(E) The electric and magnetic forces must cancel out: FE = FM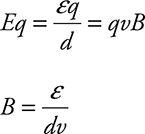
(F) The electric force remains the same, but the upward magnetic force increases because it is proportional to the velocity. Therefore, the particle will curve upward toward the top plate. Eq < q(2v)B.
(G) Because the charge cancels out of the equation, the negative particle will travel straight through without curving: Eq = qvB.
20. (A) There are many answers to this one. All we need to do is change one of the variables in the magnetic flux equation: ΦM = BAcosθ. Here are two examples: move the loop to the left, out of the magnetic field, or rotate the loop about a diameter.
(B) There are many answers. Here are two: move the magnet away from the loop, or drop the magnet through the loop.
(C) Here are two examples: rotate the magnet about its long axis as shown in the figure, or move both the magnet and the loop in the same direction at the same time, keeping the same distance between them, so there is no relative motion between them.
21. (A) To induce a current in the rectangular loop of wire, we need a change in magnetic flux. There is a change in magnetic flux only at locations 2 and 4.
(B) The flux is increasing into the page at location 2. Therefore, the current is counterclockwise to produce an out-of-the-page field to oppose the increase. At location 4, the flux is decreasing. Therefore, the current is clockwise to produce an into-the-page field to oppose the decrease in the flux.
❯ Rapid Review
• Don’t confuse magnetic and electric fields! Charged particles behave differently in each field.
• Magnetic fields can be drawn as loops going from the north pole of a magnet to the south pole.
• A long, straight, current-carrying wire creates a magnetic field that wraps around the wire in concentric circles. The direction of the magnetic field is found by a right-hand “curly fingers” rule.
• Similarly, loops of wire that carry current create magnetic fields. The direction of the magnetic field is, again, found by a right-hand rule.
• A magnetic field exerts a force on a charged particle if that particle is moving perpendicular to the magnetic field.
• When a charged particle moves perpendicular to a magnetic field, it ends up going in circles. This phenomenon is the basis behind mass spectrometry.
• A changing magnetic flux creates an induced emf, which causes current to flow in a wire.
• Lenz’s law says that when a changing magnetic flux induces a current, the direction of that current will be such that the magnetic field it induces is pointed in the opposite direction of the original change in magnetic flux.
• Domains inside ferromagnetic materials align with external magnetic fields, greatly enhancing the field. Paramagnetic materials weakly enhance external magnetic fields. Diamagnetic materials create magnetic fields that cancel the effect of external magnetic fields.
1“Yes!”