Homework Helpers: Physics

1 Kinematics

Just as displacement is the vector counterpart to the scalar quantity called distance, velocity is the vector counterpart to the scalar quantity called speed. Whereas the speed of an object can be described with only numbers and units, the velocity of an object includes direction. In other words, velocity is the speed of an object in a particular direction. For this reason, it is possible for the speed of an object to remain constant, but still have its velocity change if it changes direction.

When motion is limited to a single axis, it is more convenient to indicate the direction the object is traveling with a + or – sign. For example, instead of saying that a car has a velocity of 25.0 m/s to the south, we can say that the car has a velocity of –25.0 m/s. It is important for you to get used to the concept of using a negative sign to indicate the direction. You can”t have a negative speed, because nothing is going to move slower than stopped. A negative sign for velocity doesn”t mean “slow” (for example, –25.0 m/s indicates a faster speed than, say, +12.0 m/s); it simply means velocity in the direction opposite of what is considered positive.

What you will learn in this lesson is that the techniques that we went over for determining the resultant displacement in Lesson 1–1 work for velocity vectors as well. In fact, they work for all of the vector quantities that you will encounter while you study physics.

Before we go over some example problems, let”s make sure that you understand what velocity really is. What is the difference between displacement and velocity? Displacement is the change in an object”s position in a particular direction. Velocity is that rate at which the displacement occurs.

Velocity is usually represented by the symbol v and is typically measured in meters/second (m/s), although any unit of length or time could be substituted. The formula for determining velocity is

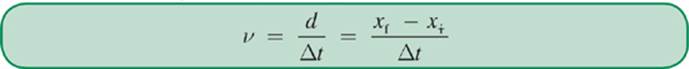
Instantaneous velocity is the velocity that an object has at a particular instant. Average velocity is the average velocity an object travels with over a period of time. These concepts should be easy to relate to their “speed” counterparts from everyday life. For example, the speedometer of a car shows the driver the instantaneous speed. If a driver covers 100 miles in two hours, his or her average speed was 50 miles per hour. When we say an object has constant velocity, we mean that its velocity is not changing. Remember: This means that the object is not speeding up, slowing down, or changing direction.

Let”s go over a few examples that will demonstrate the variety of velocity problems that you might encounter. For our first example, let”s try one that represents the simplest type of these problems.

Example 1

Find the average velocity of a ball if it rolls 30.0 m to the right in 5.0 seconds.

Given: d = 30.0 m  Δt = 5.0 s

Find: v_avg

Example 1 is simply a matter of identifying which variables you have been given and plugging them into the proper formula. Notice that our answer includes numbers, units, and a direction. Now we will try a problem that is marginally harder. For this problem you will need to be able to isolate the unknown.

Example 2

A car moves due north with a constant velocity of 30.0 m/s. How long will it take this car to travel 110 m to the north?

Given: v= 30.0 m/s d = 110 m

Find: Δt

Notice that the car is moving at constant velocity, and, in such cases, the instantaneous velocity is the same as the average velocity. We can use the same formula that we used in our last example, but we must isolate Δt.

Isolate:

For our next example, we will cover a classic example of a problem that is designed to test whether or not a student differentiates between scalar and vector quantities. Read the question carefully and make sure that you understand what is being asked.

Example 3

A race car travels completely around a circular track, covering a distance of 850 m in 25 s before stopping at the spot at which it started. Determine the average velocity of the car during this period of time.

Given: d = 0 m Δt = 25 s

Find: v_avg

Example 3 is what students call a “trick” question, and indeed, it isn”t entirely fair. Did the answer to Example 3 surprise you? Perhaps you thought that the answer was 34 m/s? The trick to this question has to do with the difference between speed and velocity. Velocity is based on displacement, and the final displacement of the race car is zero, because it ended up in the same spot in which it started. The average speed of the car, which is based on the distance traveled rather than the displacement, is equal to 34 m/s, but the average velocity is zero.

For our final example, let”s try a problem that is sometimes called a relative motion problem. Before I introduce the problem, let me explain what I mean by relative motion. Suppose I told you that it is so easy to throw a 90-mile-an-hour fastball that my 4-year-old daughter could do it. Would you believe it? What if she was sitting in the back of a van that was traveling 75 miles per hour north on a highway? If she threw a ball with a speed of 15 miles per hour north relative to the other people in the van in the same direction that the van was traveling, it would travel (75 miles/hour + 15 miles/hour) 90 miles per hour north relative to an observer standing on the road. Because the ball seems to travel at a different velocity, depending on whether or not you are inside the van, we say that its motion is relative to where the observer is.

Now, for our example.

Example 4

A child is riding in a car with a velocity of 25.0 m/s due east. The child throws a ball out the window with a velocity of 6.00 m/s south, relative to himself. What is the instantaneous velocity of the ball relative to the road?

Given: v_car = 25.0 m/s east v_toss = 6.00 m/s south

Find: v_r

Some people may be tempted to simply add the velocity of the car and the velocity at which the child threw the ball, but these vectors lie along different axes and are actually perpendicular to each other. What we need to do is add the component vectors in the same way that we added perpendicular component vectors in Lesson 1–1. When in doubt, sketch the problem out. You will see that we can solve the problem using the “tip-to-tail” method.

We can find the magnitude of the resultant velocity of the ball using the Pythagorean theorem.

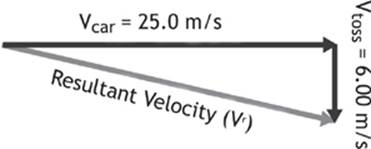
Figure 1.5

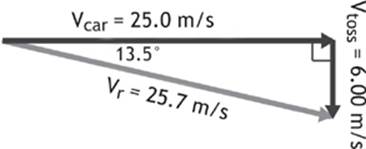
Figure 1.6

We can find the angle of this initial velocity of the ball as shown here:

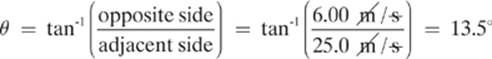
Putting this information together, we have an initial velocity of 25.7 m/s at 13.5° south of east.

Try the following practice problems and check your answers at the end of the chapter before moving on to the next lesson.

Lesson 1–2 Review

1. __________ is the speed of an object in a particular direction.

2. Is it possible for a car to move with a constant speed and still change its velocity?

3. An airplane with a velocity of 125 m/s south encounters a crosswind of 35 m/s to the west. What is the resultant velocity of the plane, relative to the ground?