Homework Helpers: Physics
1 Kinematics
Lesson 1–3: Acceleration
Just as the term velocity refers to the rate at which position changes, acceleration is the rate at which velocity changes. In other words,
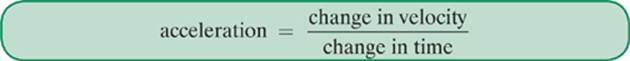
Acceleration, which we will represent with the symbol a, is measured in m/s2. The formula for velocity is
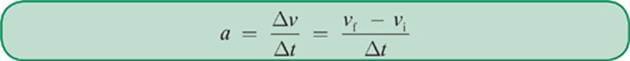
When an advertisement claims that a car can go from “zero to 60 in six seconds,” it is talking about acceleration. The term acceleration means approximately the same thing in physics as it does in everyday life with the exception that it is a vector quantity, so direction is important. If a car maintains a speed of 20.0 miles per hour as it goes around a turn, the speed is not changing, but the velocity is. Therefore, even a car moving at constant speed is said to be accelerating as it goes around a turn.
Like velocity, we can talk about the instantaneous acceleration, the acceleration at a particular instant, or the average acceleration that an object experiences over a period of time. If an object accelerates at a constant rate, we say that it moves with constant, or uniform, acceleration. When an object”s acceleration is constant, its instantaneous acceleration is the same as its average acceleration for that period of time.
One potential confusing aspect of working with acceleration is the fact that there is a difference between a deceleration (slowing down) and a negative acceleration (acceleration in the direction that has been designated as negative). Imagine a car that is heading north with a velocity of 25 m/s. We may consider north to be positive, so this would represent a positive velocity. If this car then turned around and headed south, we would consider the new velocity to be negative. If the car speeds up to the south, it would experience a negative acceleration, and the car would be going faster and faster!
When an object accelerates in the same direction as its velocity, it speeds up. When the acceleration is in the opposite direction as its velocity, the object will slow down.
Let”s take a look at the variety of acceleration questions that can be solved using the basic formula. In these examples, you won”t see references to directions such as “east” or “west.” This is because the motion will be taking place along a single axis, so we can indicate directions with + and – signs. Typically, we consider a displacement in the positive direction to be “forwards” and a displacement in the negative direction to be “backwards.”
Example 1
A car driving in a straight line accelerates from 12.0 m/s to 23.0 m/s in a period of 3.0 s. Find the average acceleration experienced by the car during this period of time.
Given: vi = 12.0 m/s vf = 23.0 m/s Δt = 3.0 s
Find: aavg
![]()
Notice that in Example 1 we had a car with a positive initial velocity and a positive acceleration, and the speed of the car increased. Let”s look at an example with a negative acceleration.
Example 2
A car with an initial velocity of 35.0 m/s experiences a constant acceleration of –7.0 m/s2. How long does it take the car to come to a complete stop?
Given: vi = 35.0 m/s vf = 0.0 m/s a = −7.0 m/s2
Find: Δt
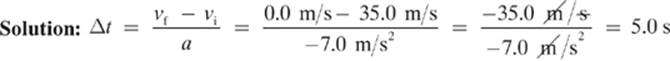
Example 2 shows how important it is to subtract the initial velocity from the final velocity (Δv = vfinal − vinitial) to find the change in velocity. Some students would reverse this calculation, subtracting the final velocity from the initial. In a problem such as Example 2, this would yield a positive value for Δv and a negative value for Δt! Unless your teacher gives you a problem on time travel, and I wouldn”t put that past some physics teachers, you shouldn”t end up with a negative change in time.
Now, let”s try an example with a negative velocity and a positive acceleration, just to reinforce the importance of the algebraic signs. Try this problem on paper by yourself before looking ahead to my answer.
Example 3
A motorcycle with an initial velocity of −21.0 m/s experiences a constant acceleration of 4.00 m/s2 for a period of 3.0 s. What will be the final velocity of the motorcycle?
Given: vi = −21.0m/s a = 400m/s2 Δt = 3.0s
Find: vf
The first key to Example 3 is to note that the initial velocity is negative, but the acceleration is positive. This will result in the motorcycle slowing down, not speeding up. If you end up with a greater final velocity, then you probably mixed up the algebraic signs. The other thing that some people might find challenging is the isolation of the unknown, vf, as shown here:
Isolate:
![]()
Multiply both sides by Δt and it cancels on the right side:
![]()
This gives us: Δt × a = vf – vi
Now, add vi to both sides of the equation, and cancel:
![]()
Rearranging the formula, we get: vf = vi + aΔt
This working formula, vf = vi + aΔt, is one that you should become familiar with. It will be useful for solving a large number of problems. Now that we have this working formula, we are ready to solve example 3. Compare your answer to the one shown here:
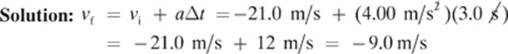
Notice that the motorcycle experiences a positive acceleration, and slows down. This occurs because the velocity and acceleration were in opposite directions. Let”s try one more example together, before moving on to the practice problems.
Example 4
A horse starts from rest and accelerates at an average rate of –2.5 m/s2 over a period of 7.0 s. What is the final velocity of the horse after this time?
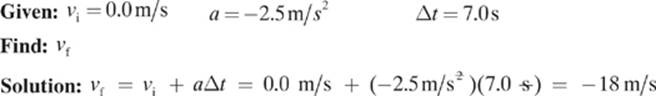
Does the negative value for the horse”s velocity in Example 4 imply that the horse is running backwards? No, it is simply heading in the direction opposite to what is considered positive in this particular problem.
Now let”s move on to the practice problems. Remember to check your answers with the Answer Key.
Lesson 1–3 Review
1. _______________ is the rate at which an object”s velocity changes.
2. An airplane with an initial velocity of 0.0 m/s experiences a uniform acceleration of 9.5 m/s2. How much time will it take to reach a velocity of 125 m/s?
3. Is it possible for an object to speed up while experiencing a negative acceleration?
4. If a car goes around a turn while traveling at a constant speed of 15.0 miles per hour, is it accelerating?
5. A car with an initial velocity of 18.0 m/s experiences an acceleration of –2.50 m/s2 for a period of 3.50 s. What is the final velocity of the car?