SAT Test Prep
CHAPTER 11
ESSENTIAL ALGEBRA 2 SKILLS
Lesson 4: Variation
Direct Variation
The statement “y varies directly as x” means that the variables are related by the equation ![]() , where k is a non-zero constant. This equation implies that x and y go up and down proportionally. For instance, whenever x is multiplied by 3, y is also multiplied by 3.
, where k is a non-zero constant. This equation implies that x and y go up and down proportionally. For instance, whenever x is multiplied by 3, y is also multiplied by 3.
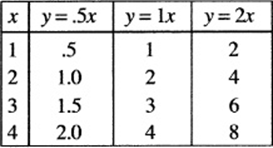
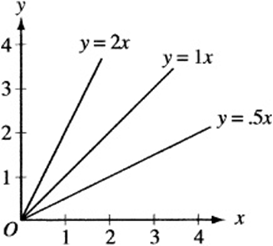
The table and graph above show three examples of direct variation functions. Notice that (1) every graph passes through the origin, (2) as k increases, so does the slope of the graph, and (3) for any given k, whenever x is doubled (or tripled or halved), so is the corresponding value of y.
Example:
If x varies directly as y and ![]() when
when ![]() , then what is the value of x when
, then what is the value of x when ![]()
First find the value of the constant k by substituting the values of x and y into the equation ![]() .
.

Now we know that the equation is ![]() .
.
Inverse Variation
The statement “y varies inversely as x” means that the variables are related by the equations ![]() or
or ![]() , where k is a non-zero constant.
, where k is a non-zero constant.
These equations imply that x and y go up and down inversely. For instance, whenever x is multiplied by 3, y is divided by 3.
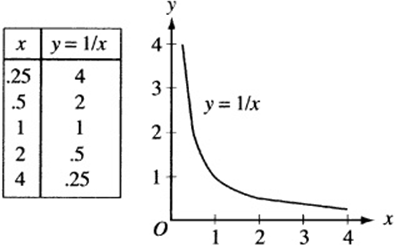
The table and graph above show an example of an inverse variation function. Notice that (1) the graph never touches the x-or y-axis, (2) as x increases, y decreases, and (3) for every point on the graph, the product of x and y is always the constant k, in this case ![]() .
.
Example:
If x varies inversely as y and ![]() when
when ![]() , then what is the value of x when
, then what is the value of x when ![]() ?
?
First find the value of the constant k by substituting the values of x and y into the equation ![]() .
.

Now we know that the equation is ![]() .
.

Joint and Power Variation
A variable can vary with more than one other variable or with powers of a variable. For instance, the statement “y varies directly as x and inversely as w” means that ![]() , and “y varies inversely as the square of x” means that
, and “y varies inversely as the square of x” means that 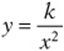
Concept Review 4: Variation
1. What equation is equivalent to the statement y varies directly as the square of x?
2. If y varies inversely as x, then the ________________ of x and y is a constant.
3. If y varies directly as x, then the ________________ of x and y is a constant.
4. Describe the features of the graph of a direct variation function.
5. If w varies directly as v3 and ![]() when
when ![]() , what is the value of w when
, what is the value of w when ![]() ?
?
6. If y varies inversely as the square of x, then what will be the effect on y if the value of x is doubled?
7. The variable a varies inversely as b. If ![]() when
when ![]() , then for how many ordered pairs (a, b) are both a and b positive integers?
, then for how many ordered pairs (a, b) are both a and b positive integers?
8. If x varies directly as the square root of y and directly as z, and if ![]() when
when ![]() and
and ![]() , what is the value of z when
, what is the value of z when ![]() and
and ![]() ?
?
SAT Practice 4: Variation
1. If p varies inversely as q and ![]() when
when ![]() , then which of the following represents another possible solution for p and q?
, then which of the following represents another possible solution for p and q?
![]() and
and ![]()
![]() and
and ![]()
![]() and
and ![]()
![]() and
and ![]()
![]() and
and ![]()
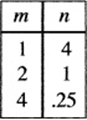
2. Which of the following describes one possible relationship between the values of m and n shown in the table above?
(A) n varies directly as m
(B) n varies inversely as m
(C) n varies directly as the square of m
(D) n varies inversely as the square of m
(E) n varies directly as the square root of m
3. If the function f is defined by the equation ![]() and
and ![]() , what is the value of f (2a, 2b)?
, what is the value of f (2a, 2b)?
(A) 50
(B) 100
(C) 160
(D) 320
(E) 640
4. At a fixed temperature, the volume of a sample of gas varies inversely as the pressure of the gas. If the pressure of a sample of gas at a fixed temperature is increased by 50%, by what percent is the volume decreased?
(A) 25%
![]()
(C) 50%
(D) 75%
(E) 100%
5. The force of gravity between two stars varies inversely as the square of the distance between the stars. If the force of gravity between two stars that are four light-years apart is 64 exanewtons (1 exanewton = 1018 newtons), what would the force between these stars be if they were eight light-years apart?
(A) 256 exanewtons
(B) 128 exanewtons
(C) 32 exanewtons
(D) 16 exanewtons
(E) 8 exanewtons
6. If the variable a varies directly as b and inversely as c, and if ![]() when
when ![]() and
and ![]() , then what is the value of a when
, then what is the value of a when ![]() and
and ![]()

7. If the variable y varies inversely as the square of x, and if ![]() , then which of the following operations will double the value of y?
, then which of the following operations will double the value of y?
(A) multiplying x by 2
(B) dividing x by 2
(C) multiplying x by ![]()
(D) dividing x by ![]()
(E) dividing x by 4
8. If ![]() when
when ![]() and
and ![]() when
when ![]() , which of the following could express the relationship between x and y?
, which of the following could express the relationship between x and y?
I. y varies inversely as x
II. y varies directly as the square of x
III. y varies directly as x
(A) none
(B) I only
(C) I and II only
(D) I and III only
(E) I, II, and III
Answer Key 4: Variation
Concept Review 4
1. y = kx2
2. product
3. quotient or ratio
4. It is a straight line passing through the origin with a slope equal to k, the constant of proportionality. For every point on the line, the ratio of the y coordinate to the x coordinate is equal to k.
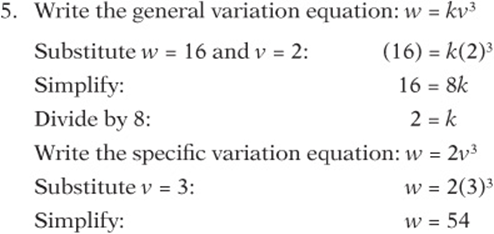

So what was the effect on y when you doubled the value of x? It went from 3 to 3/4, therefore, it was divided by 4 or multiplied by 1/4.
7. If a varies inversely as b, then ![]() , where k is a constant. If
, where k is a constant. If ![]() when
when ![]() , then
, then ![]() . Therefore, in any ordered pair solution (a, b), the product of a and b must be 16. The only solutions in which a and b are both positive integers are (1, 16), (2, 8), (4, 4), (8, 2), and (16, 1), for a total of five ordered pairs.
. Therefore, in any ordered pair solution (a, b), the product of a and b must be 16. The only solutions in which a and b are both positive integers are (1, 16), (2, 8), (4, 4), (8, 2), and (16, 1), for a total of five ordered pairs.
8. If x varies directly as the square root of y and directly as z, then ![]() . First, substitute the values
. First, substitute the values ![]() ,
, ![]() , and
, and ![]() to find k:
to find k:
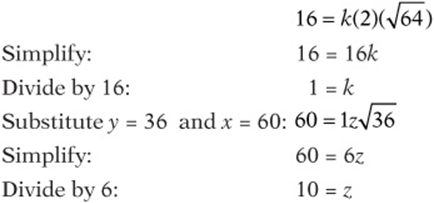
SAT Practice 4
1. E Recall from the lesson that whenever two variables vary inversely, they have a constant product. The product of 4 and 6 is 24, so every other correct solution for p and q must have a product of 24 also. Choice (E) is the only one that gives values that have a product of 24.
2. D It helps first to notice from the table that as m increases, n decreases, so any variation relationship must be an inverse variation. Therefore, only choices (B) and (D) are possibilities. If n varied inversely as m, then the two variables would always have the same product, but this is not the case: ![]() ,
,![]() , and
, and ![]() . However, if n varied inversely as the square of m, then n and m2would always have the same product. This is true:
. However, if n varied inversely as the square of m, then n and m2would always have the same product. This is true: ![]() ,
, ![]() and
and ![]() . Therefore, the correct answer is (D).
. Therefore, the correct answer is (D).
3. D You are given that ![]() . Using the definition,
. Using the definition, ![]() . Substituting
. Substituting ![]() , you get
, you get ![]() .
.
4. B It”s probably easiest to set up the equation, then choose simple values for the volume and pressure, and then “experiment.” Since the volume varies inversely as the pressure, the product of the volume and the pressure is a constant:![]() . Now choose simple values for v and p, such as 2 and
. Now choose simple values for v and p, such as 2 and ![]() . Therefore, in this case, the product of the volume and the pressure is always 8. If the pressure is increased 50%, then it grows to
. Therefore, in this case, the product of the volume and the pressure is always 8. If the pressure is increased 50%, then it grows to ![]() . Now solve for the corresponding value of v:
. Now solve for the corresponding value of v:
![]()
Divide by 6:
![]()
Therefore, the volume has decreased from 2 to ![]() . To calculate the percent decrease, use the “percent change” formula from Chapter 7, Lesson 5:
. To calculate the percent decrease, use the “percent change” formula from Chapter 7, Lesson 5:
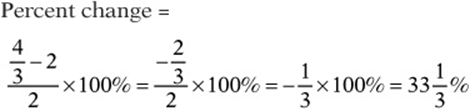
5. D If the force varies inversely as the square of the distance, then the product of the force and the square of the distance is a constant. For these particular stars, the force times the square of the distance is ![]() . If they were eight light-years apart, then the force would satisfy the equation
. If they were eight light-years apart, then the force would satisfy the equation ![]() , so
, so ![]() .
.
6. 4 Set up the variation equation:
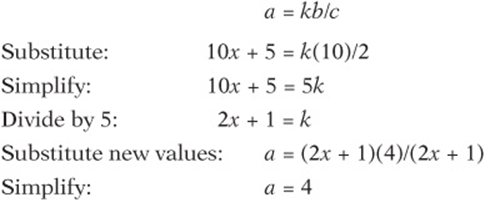
7. D If y varies inversely as the square of x, then their product x2y is a constant. To keep it simple, pick x and y to be 1, so the product ![]() . To find the value of x that would double y, simply double y and solve for x.
. To find the value of x that would double y, simply double y and solve for x.
If ![]() , then
, then ![]() This is the original value of x divided by
This is the original value of x divided by ![]() .
.
8. B Since y increases as x decreases, any variation must be an inverse variation. Since the product of x and y is a constant ![]() , y varies inversely as x.
, y varies inversely as x.