Part III. QUANTITATIVE REASONING

Chapter 11. Quantitative Comparison

Introduction to Quantitative Comparison

In each Quantitative Comparison question, you’ll see two mathematical expressions. One is Quantity A, and the other is Quantity B. You will be asked to compare them. Some questions include additional centered information. This centered information applies to both quantities and is essential to making the comparison. Since this type of question is about the relationship between the two quantities, you usually won’t need to calculate a specific value for either quantity. Therefore, you do not want to rely on the onscreen calculator to answer these questions.

The directions for a Quantitative Comparison question will look like this:

·        Directions: Select the correct answer.

The Kaplan Method for Quantitative Comparison

1.    STEP 1Analyze the centered information and quantities.

2.    STEP 2Approach strategically.

HOW THE KAPLAN METHOD FOR QUANTITATIVE COMPARISON WORKS

Now let’s discuss how the Kaplan Method for Quantitative Comparison works.

1.     STEP 1
Analyze the centered information and the quantities.

Notice whether the quantities contain numbers, variables, or both. If there is centered information, decide how it affects the information given in the quantities. Note that a variable has the same value each time it appears within a question.

2.     STEP 2
Approach strategically.

Think about a strategy you could use to compare the quantities now that you’ve determined the information you have and the information you need. There are a variety of approaches to solving a Quantitative Comparison question, and the practice examples will take you through several of these.

HOW TO APPLY THE KAPLAN METHOD FOR QUANTITATIVE COMPARISON

Now let’s apply the Kaplan Method to a Quantitative Comparison question:

·         

Quantity A	Quantity B

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

1.     STEP 1
Analyze the centered information and the columns.

This problem would be a nightmare to calculate under timed conditions. But the only thing you need to figure out is whether one quantity is greater than the other. One thing you might notice is that choice (D) is not an option here. Because both quantities contain only numbers, there is a definite value for each quantity, and a relationship can be determined. Answer choice (D) is never correct when the quantities contain only numbers.

Note that the quantity on the left is the same as the quantity in the denominator of the fraction on the right. You can think about this problem as a comparison of x and  (or the reciprocal of x), where x has a definite value. Your job now is to figure out just how to compare them.

2.     STEP 2
Approach strategically.

Before you start to do a long calculation, think about what you already know. While you may not know the sum of the four fractions, you do know two things: and  and  are each less than  Because the reciprocal of any number between 0 and 1 is greater than 1, and Quantity A is a positive number less than 1, its reciprocal in Quantity B is greater than 1. So choice (B) is correct. Quantitative Comparisons rarely, if ever, ask for exact values, so don’t waste time calculating them.

Now let’s apply the Kaplan Method to a second Quantitative Comparison question:

·        w > x > 0 > y > z

Quantity A	Quantity B
w + y	x + z

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

1.     STEP 1
Analyze the centered information and the quantities.

In this problem, there are four variables: w, x, y, and z. You are asked to compare the values of the sums of pairs of variables. You know the relative values of the different variables, but you don’t know the actual amounts. You do know that two of the variables (w and x) must be positive and two of the variables (y and z) must be negative numbers.

2.     STEP 2
Approach strategically.

In this case, think about the different sums as pieces of the whole. If every “piece” in one quantity is greater than a corresponding “piece” in the other quantity, and if the only operation involved is addition, then the quantity with the greater individual values will have the greater total value. From the given information, we know the following:

·        w > x

·        y > z

The first term, w, in Quantity A is greater than the first term, x, in Quantity B. Similarly, the second term, y, in Quantity A is greater than the second term, z, in Quantity B. Because each piece in Quantity A is greater than the corresponding piece in Quantity B, Quantity A must be greater; the answer is (A).

Now let’s apply the Kaplan Method to a third Quantitative Comparison question:

·        The diameter of circle O is d, and the area is a.

Quantity A	Quantity B
	a

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

1.     STEP 1
Analyze the centered information and the quantities.

In this problem, you are given additional information: the sentence that tells you the diameter of circle O is d and the area is a. This is important information because it gives you a key to unlocking this question. Given that information, you can tell that you are comparing the area, a, of circle O and a quantity that includes the diameter of the same circle. If you’re thinking about the formula for calculating area given the diameter, you’re thinking right!

2.     STEP 2
Approach strategically.

Make Quantity B look more like Quantity A by rewriting a, the area of the circle, in terms of the diameter, d. The area of any circle equals πr², where r is the radius. Because the radius is half the diameter, you can substitute  for r in the area formula to get  in Quantity B. Simplifying, you get 

Because both quantities contain π, we could compare  to  But let’s take it one step further. You know that d is a distance and must be a positive number. That makes it possible to divide both quantities,  and  by d² and then just compare  to  . This makes it easy to see that Quantity A is always greater because  Choice (A) is correct.

Kaplan’s Additional Tips for Quantitative Comparison Questions

Memorize the Answer Choices

It is a good idea to memorize what the Quantitative Comparison answer choices mean. This is not as difficult as it sounds. The choices are always the same. The wording and the order never vary. As you work through the practice problems, the choices will become second nature to you, and you will get used to reacting to the questions without reading the four answer choices, thus saving you lots of time on Test Day.

When there is at least one variable in a problem, try to demonstrate two different relationships between quantities

Here’s why demonstrating two different relationships between the quantities is an important strategy: if you can demonstrate two different relationships, then choice (D) is correct. There is no need to examine the question further.

But how can this demonstration be done efficiently? A good suggestion is to look at the expression(s) containing a variable and notice the possible values of the variable given the mathematical operation involved. For example, if x can be any real number and you need to compare (x + 1)² to (x + 1), pick a value for x that will make (x + 1) a fraction between 0 and 1 and then pick a value for x that will make (x + 1) greater than 1. By choosing values for x in this way, you are basing your number choices on mathematical properties you already know: a positive fraction less than 1 becomes smaller when squared, but a number greater than 1 grows larger when squared.

Compare quantities piece by piece

Compare the value of each “piece” in each quantity. If every “piece” in one quantity is greater than a corresponding “piece” in the other quantity, and the operation involved is either addition or multiplication, then the quantity with the greater individual values will have the greater total value.

Make one quantity look like the other

When the Quantities A and B are expressed differently, you can often make the comparison easier by changing the format of one quantity so that it looks like the other. This is a great approach when the quantities look so different that you can’t compare them directly.

Do the same thing to both quantities

If the quantities you are given seem too complex to compare immediately, look closely to see if there is an addition, subtraction, multiplication, or division operation you can perform on both quantities to make them simpler—provided you do not multiply or divide by zero or a negative number. For example, suppose you have the task of comparing  to , where w is greater than 0. To get to the heart of the comparison, subtract 1 from both quantities and you have  compared to  To simplify even further, multiply both quantities by (1 + w), and then you can compare w to 1.

Don’t be tricked by misleading information

To avoid Quantitative Comparison traps, stay alert and don’t assume anything. If you are using a diagram to answer a question, use only information that is given or information that you know must be true based on properties or theorems. For instance, don’t assume angles are equal or lines are parallel unless it is stated or can be deduced from other information given.

A common mistake is to assume that variables represent only positive integers. As you saw when using the Picking Numbers strategy, fractions or negative numbers often show a different relationship between the quantities.

Don’t forget to consider other possibilities

If an answer looks obvious, it may very well be a trap. Consider this situation: a question requires you to think of two integers whose product is 6. If you jump to the conclusion that 2 and 3 are the integers, you will miss several other possibilities. Not only are 1 and 6 possibilities, but there are also pairs of negative integers to consider: −2 and −3, −1 and −6.

Don’t fall for look-alikes

Even if two expressions look similar, they may be mathematically different. Be especially careful with expressions involving parentheses or radicals. If you were asked to compare to  you would not want to fall into the trap of saying the two expressions were equal. Although time is an important factor in taking the GRE, don’t rush to the extent that you do not apply your skills correctly. In this case,  which is not the same as  unless x = 0.

Quantitative Comparison Practice Set

Try the following Quantitative Comparison questions using the Kaplan Method for Quantitative Comparison. If you’re up to the challenge, time yourself: on Test Day, you’ll want to spend only 1.5 minutes on each question.

1.     

1.     

Quantity A	Quantity B
x2 + 2x − 2	x2 + 2x − 1

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

2.    x = 2y; y is a positive integer.

Quantity A	Quantity B
42y	2x

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

3.    q, r, and s are positive numbers; qrs > 12.

Quantity A	Quantity B

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

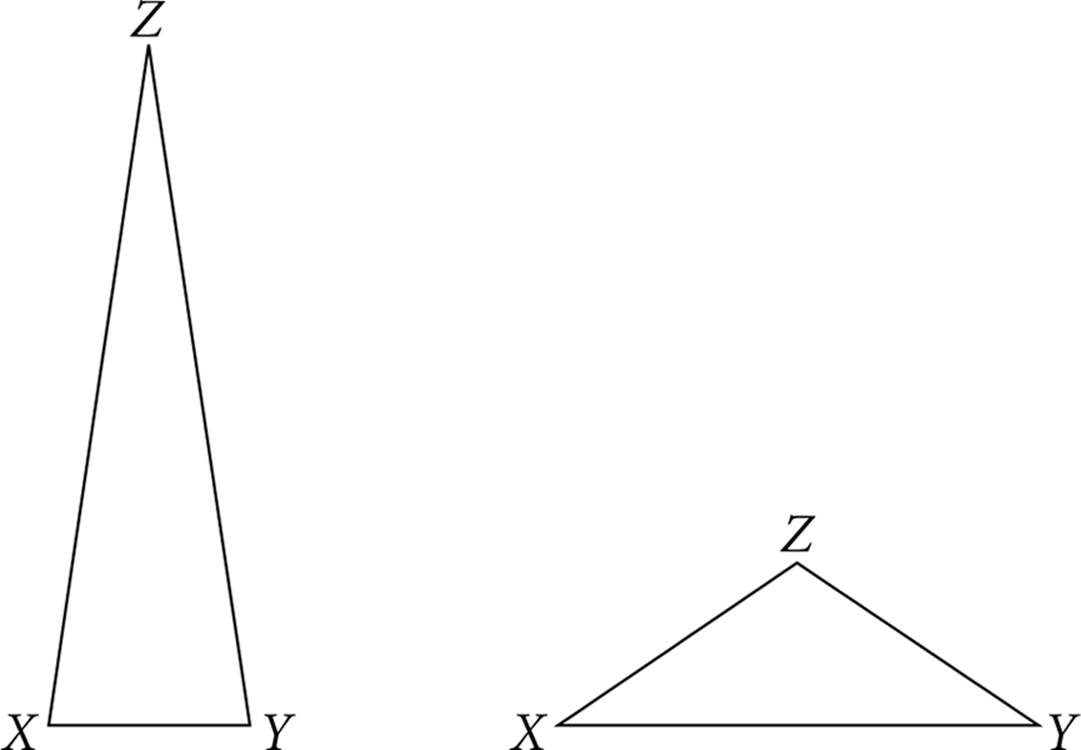
4.    In triangle XYZ not given, the measure of angle X equals the measure of angle Y.

Quantity A	Quantity B
The degree measure of angle Z	The degree measure of angle X plus the degree measure of angle Y

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

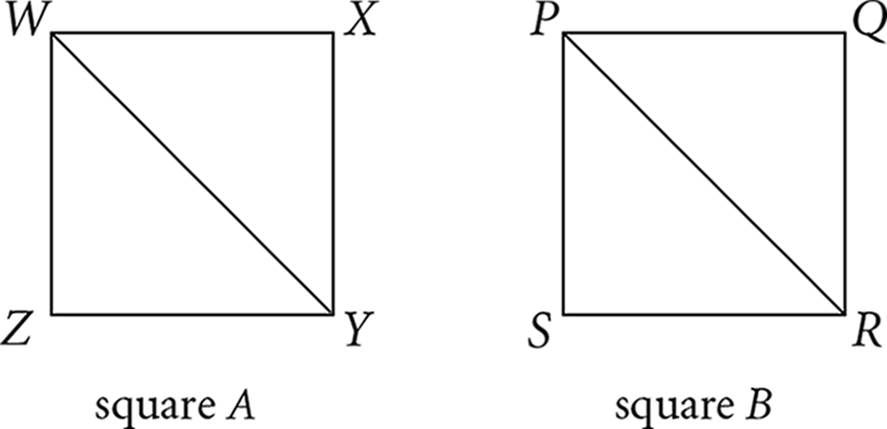
5.   

5.     

Quantity A	Quantity B

1.    Quantity A is greater.

2.    Quantity B is greater.

3.    The two quantities are equal.

4.    The relationship cannot be determined from the information given.

Answers and Explanations

QUANTITATIVE COMPARISON PRACTICE SET

1.    BComparing the two quantities piece by piece, you find that the only difference is the third piece: −2 in Quantity A and −1 in Quantity B. You don’t know the value of x, but whatever it is, x² in Quantity A must have the same value as x² in Quantity B, and 2x in Quantity A must have the same value as 2x in Quantity B. Because any quantity minus 2 must be less than that quantity minus 1, Quantity B is greater than Quantity A. The correct choice is (B).

2.    AReplacing the exponent x in Quantity B with the equivalent value given in the centered information, you’re comparing 4²y with 2²y. Because y is a positive integer, raising 4 to the exponent 2y will result in a greater value than raising 2 to the exponent 2y. The correct choice is (A).

3.    D

Do the same thing to both quantities to make them look like the centered information. When you multiply both quantities by 5s, you get qrs in Quantity A and 15 in Quantity B. Because qrs could be any integer greater than 12, qrs could be greater than, equal to, or less than 15. Choice (D) is correct.

4.    DBecause angle X = angle Y, at least two sides of the triangle are equal. You can draw two diagrams with X and Y as the base angles of a triangle. In one diagram, make the triangle tall and narrow so that angle X and angle Y are very large and angle Z is very small. In this case, Quantity B is greater. In the second diagram, make the triangle short and wide so that angle Z is much larger than angle X and angle Y. In this case, Quantity A is greater. Because more than one relationship between the quantities is possible, the correct answer is (D).

5.    C

You don’t know the exact relationship between square A and square B, but it doesn’t matter. The problem is actually just comparing the ratios of corresponding parts of two squares. The relationship between the specific side lengths of both squares will also exist between them for any other corresponding length. If a side of one square is twice the length of a side of the second square, the diagonal will also be twice as long. The ratio of the perimeters of the two squares is the same as the ratio of the diagonals.

You can make this abstract relationship concrete by Picking Numbers for the sides of the two squares. Say, for example, that each side of square A is 2 and each side of square B is 3. Then the ratio of the perimeters is 8:12 or 2:3, and the ratio of the diagonals is . Therefore, the quantities are equal. Choice (C) is correct.