GRE Premier 2017 with 6 Practice Tests
Part III. QUANTITATIVE REASONING
Chapter 12. Problem Solving
Introduction to Problem Solving
Problem Solving can be broken up into several general mathematics categories: algebra, arithmetic, number properties, and geometry.
In a Problem Solving question, you may be asked to solve a pure math problem or a word problem involving a real-world situation. You will be asked to enter your answer into an onscreen box, select one answer, or select one or more options that correctly answer the problem.
The directions for a Problem Solving question requiring a single answer will look like this:
· Directions: Click to select your choice.
A Problem Solving question requiring you to select a single answer will look like this, with ovals next to each answer choice:

The directions for a Problem Solving question requiring you to select one or more answers will look like this:
· Directions: Click to select your choice(s).
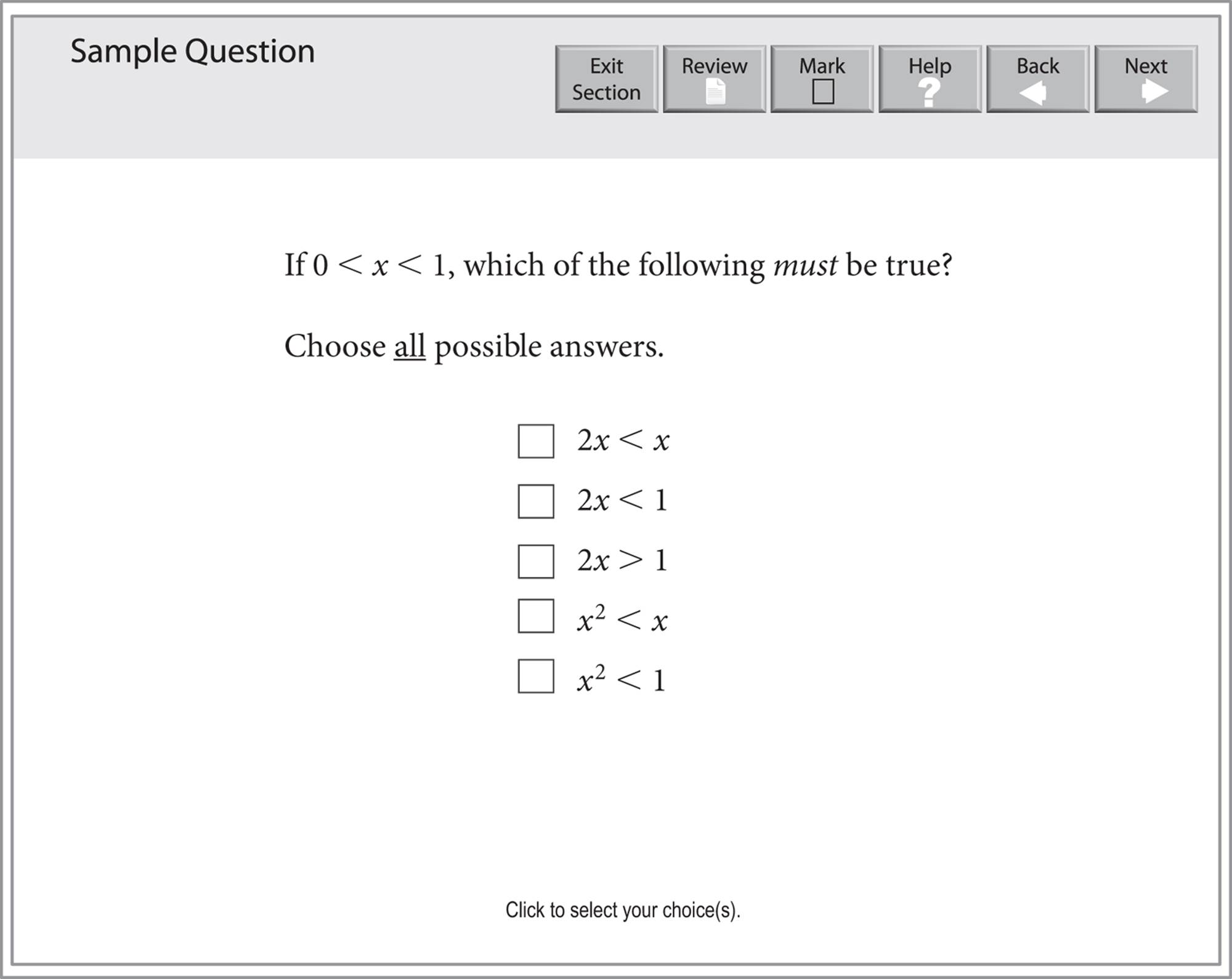
If a Problem Solving question asks you to select your choice(s), at least one answer is correct, but as many as all the choices may be correct. You must select all of the correct choices (and none of the incorrect ones) for the question to be counted as correct.
A Problem Solving question requiring you to select one or more answers will look like this, with rectangles next to each answer choice:
The directions for a Problem Solving question requiring you to make a Numeric Entry will look like this:
· Directions: Click in the box and type your numeric answer. Backspace to erase.
Enter your answer as an integer or decimal if there is one box or as a fraction if there are two boxes.
To enter an integer or decimal, type directly in the box or use the Transfer Display button on the calculator.
· Use the backspace key to erase.
· Use a hyphen to enter a negative sign; type a hyphen a second time to remove it. The digits will remain.
· Use a period for a decimal point.
· The Transfer Display button will enter your answer directly from the calculator.
· Equivalent forms of decimals are all correct. (Example: 0.14 = 0.140)
· Enter the exact answer unless the question asks you to round your answer.
To enter a fraction, type the numerator and denominator in the appropriate boxes.
· Use a hyphen to enter a negative sign.
· The Transfer Display button does not work for fractions.
· Equivalent forms of fractions are all correct. (Example: ![]() If numbers are large, reduce fractions to fit in boxes.
If numbers are large, reduce fractions to fit in boxes.
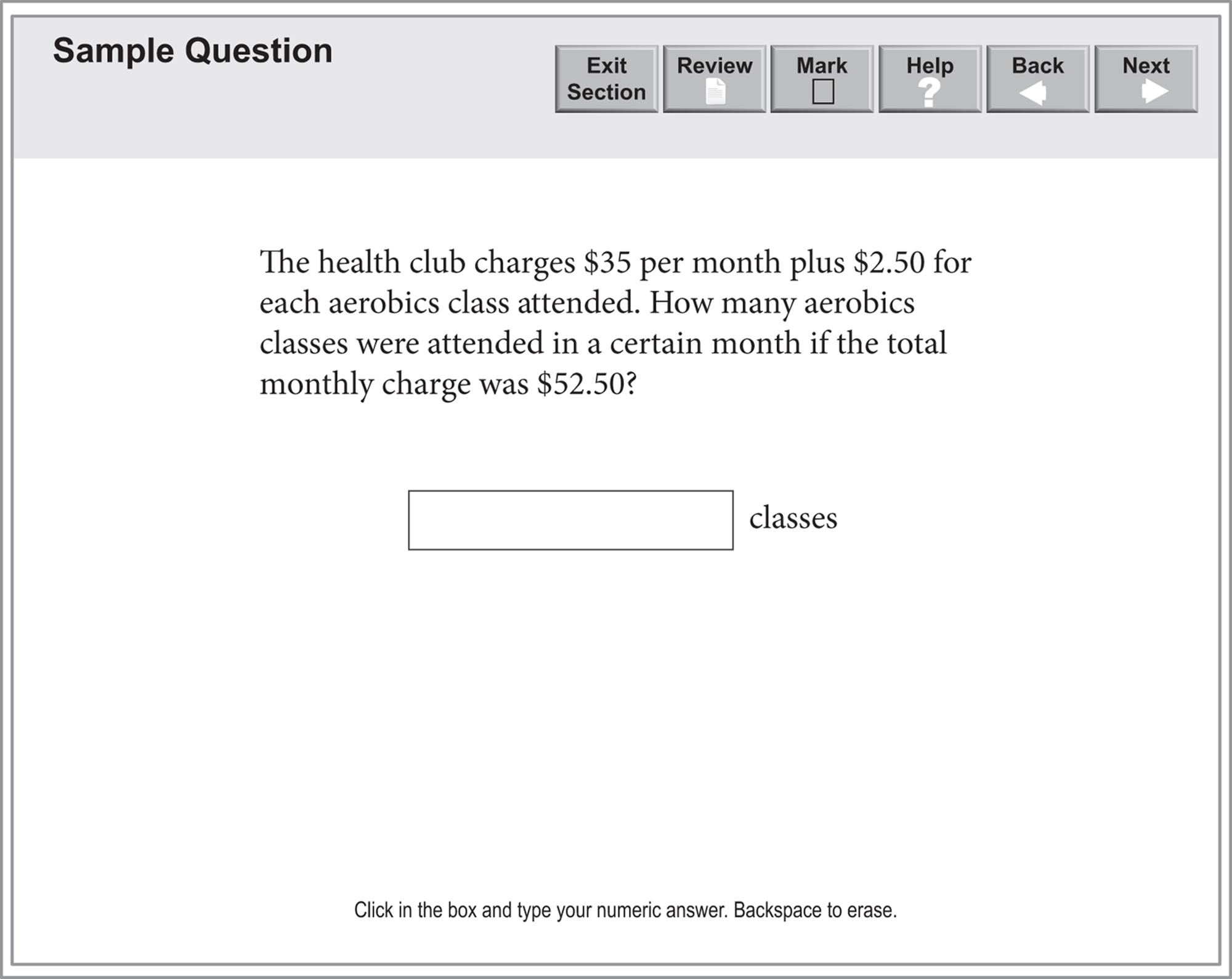
A Problem Solving question with Numeric Entry will look like this:
The Kaplan Method for Problem Solving
1. STEP 1Analyze the question.
2. STEP 2Identify the task.
3. STEP 3Approach strategically.
4. STEP 4Confirm your answer.
HOW THE KAPLAN METHOD FOR PROBLEM SOLVING WORKS
Now let’s discuss how the Kaplan Method for Problem Solving works:
1. ![]() STEP 1
STEP 1
Analyze the question.
Look at what the question is asking and what area of math is being tested. Also note any particular trends in the answer choices (e.g., numbers/variables, integers/non-integers) and what information is being given. Unpack as much information as possible.
2. ![]() STEP 2
STEP 2
Identify the task.
Determine what question is being asked before solving the problem. Ask yourself, “What does the correct answer represent?” The GRE intentionally provides wrong answers for test takers who get the right answer to the wrong question.
3. ![]() STEP 3
STEP 3
Approach strategically.
Depending on the type of problem, you may use straightforward math—the textbook approach—to calculate your answer, or you may choose one of the following strategies: Picking Numbers, Backsolving, or Strategic Guessing.
When Picking Numbers to substitute for variables, choose numbers that are manageable and fit the description given in the problem. Backsolving is another form of Picking Numbers; you’ll start with one of the answer choices and plug that choice back into the question. Lastly, Strategic Guessing can be a great time-saver on the GRE—being able to make a smart guess on a question is preferable to taking too much time and thus compromising your ability to answer other questions correctly.
4. ![]() STEP 4
STEP 4
Confirm your answer.
Check that your answer makes sense. Also check that you answered the question that was asked.
HOW TO APPLY THE KAPLAN METHOD FOR PROBLEM SOLVING
Now let’s apply the Kaplan Method to a Problem Solving question:
· In a bag of candy, 7 of the candies are cherry flavored, 8 are lemon, and 5 are grape. If a candy is chosen randomly from the bag, what is the probability that the candy is not lemon?
1. ![]() STEP 1
STEP 1
Analyze the question.
You are given the number of candies in a bag and asked to identify the probability that a randomly selected candy is not lemon flavored. You will have to type your answer into the box.
2. ![]() STEP 2
STEP 2
Identify the task.
The probability of an event is defined as ![]() You will need to find the number of desired outcomes (those in which you don’t choose a lemon candy) and the total number of possible outcomes.
You will need to find the number of desired outcomes (those in which you don’t choose a lemon candy) and the total number of possible outcomes.
3. ![]() STEP 3
STEP 3
Approach strategically.
There are 20 candies in the bag, so there are 20 possible outcomes. Of all the candies, 12 are not lemon, so there are 12 desired outcomes. So, the probability of not lemon is ![]() You should avoid reducing fractions for Numeric Entry questions, since all equivalent forms will be counted as correct. Save your time for other questions and limit your risk of committing an error in calculation.
You should avoid reducing fractions for Numeric Entry questions, since all equivalent forms will be counted as correct. Save your time for other questions and limit your risk of committing an error in calculation.
4. ![]() STEP 4
STEP 4
Confirm your answer.
Although it might be fun to get a bag of candies and check your answer in a real-world way, it’s not practical, especially on Test Day. A more practical check would be to find the probability of choosing a lemon candy at random to be certain that P(lemon) = 1 − P(not lemon). There are 8 lemon candies out of 20, so this check can be done easily.
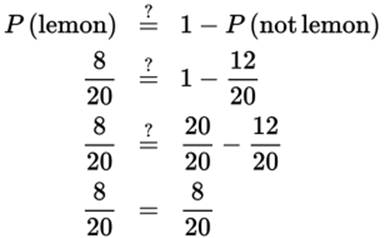
This check is a way to confirm that the correct numbers have been used in the problem and the correct answer has been found.
Now let’s apply the Kaplan Method to a second Problem Solving question:
· When n is divided by 14, the remainder is 10. What is the remainder when n is divided by 7?
1. 2
2. 3
3. 4
4. 5
5. 6
1. ![]() STEP 1
STEP 1
Analyze the question.
In this question, you are asked to compare the relationship between the numbers 14 and 7 used as divisors.
2. ![]() STEP 2
STEP 2
Identify the task.
The task is to use the fact that division of a number, n, by 14 yields a remainder of 10 to identify the remainder when the same number is divided by 7.
3. ![]() STEP 3
STEP 3
Approach strategically.
A good strategy for this question is to pick a number for n that satisfies the condition for division by 14 and then see what happens when it is divided by 7.
Any number divided by itself will give a remainder of zero. So if we need a remainder of 10, we want a number that is 10 more than the number we are dividing by. Be careful; you may be thinking of choosing 14 ÷ 7 = 2 or 10 ÷ 2 = 5. But these are both trap answer choices because the question also involves using a remainder. Therefore, 24 is a great number to pick here, because when we try 24:
24 ÷ 14 = 1 Remainder 10
Now that we’ve confirmed that 24 works, we answer the question that’s being asked. Divide 24 by 7:
24 ÷ 7 = 3 Remainder 3
Answer choice (B) is the correct answer.
4. ![]() STEP 4
STEP 4
Confirm your answer.
You can quickly double-check your work, or you can try another number for n that results in a remainder of 10 when divided by 14:
38 ÷ 14 = 2 Remainder 10, and 38 ÷ 7 = 5 Remainder 3
So the remainder is 3 in each case. The correct answer is (B).
Now let’s apply the Kaplan Method to a third Problem Solving question:
· The line 4x + 6y = 24 passes through which of the following points?
Indicate all possible answers.
1. (0, 4)
2. (2, 3)
3. (3, 2)
4. (5, 4)
5. (9, −1)
1. ![]() STEP 1
STEP 1
Analyze the question.
This question is about a line on the coordinate plane. The equation is a function that represents a line. The numbers in the parentheses in the answer choices represent points (x, y) that are mentioned in the equation.
2. ![]() STEP 2
STEP 2
Identify the task.
Your job is to identify which of the given points lie on the line. A line passes through a point if the coordinates of the point make the equation of the line true, so this is the same as saying that you need to find out which point(s), when plugged into the equation, make the equation true.
3. ![]() STEP 3
STEP 3
Approach strategically.
You need to find all correct answers, so test all of them. Substitute the first coordinate for x and the second coordinate for y.
·
1. Test (0, 4): 4x + 6y = 24 → 4(0) + 6(4) = 0 + 24 = 24. This works.
2. Test (2, 3): 4x + 6y = 24 → 4(2) + 6(3) = 8 + 18 ≠ 24. Eliminate.
3. Test (3, 2): 4x + 6y = 24 → 4(3) + 6(2) = 12 + 12 = 24. This works.
4. Test (5, 4): 4x + 6y = 24 → 4(5) + 6(4) = 20 + 24 ≠ 24. Eliminate.
5. Test (9, –1): 4x + 6y = 24 → 4(9) + 6(−1) = 36 – 6 ≠ 24. Eliminate.
So choices (A) and (C) are correct.
1. ![]() STEP 4
STEP 4
Confirm your answer.
Double-check your work to make sure you haven’t made any careless errors, such as mistakenly plugging in a value for x when dealing with the variable y.
Kaplan’s Additional Tips for Problem Solving
Choose an efficient strategy
The GRE is not a traditional math test that requires that you show your work in order to get credit, testing the process as well as the answer. The GRE tests only the answer—not how you found it. Because time is often your biggest concern on the GRE, the best way to each solution is often the quickest way, and the quickest way is often not straightforward math. Through practice, you’ll become familiar with approaching each question in a more strategic way.
Rely on Kaplan math strategies
Using Kaplan strategies is a way to use reasoning in conjunction with mathematics to answer a question quickly. There may also be cases in which you can combine approaches: for example, using straightforward math to simplify an equation, then picking manageable numbers for the variables to solve that equation.
Picking numbers
Problems that seem difficult can be good candidates for the Picking Numbers strategy. They include problems where either the question or the answer choices have variables, the problem tests a number property you don’t recall, or the problem and the answer choices deal with percents or fractions without using actual values.
Backsolving
Backsolving is a similar strategy to Picking Numbers, except that you’ll use one of the five answer choices as the number to pick. After all, the testmaker gives you the correct answer; it's just mixed in with the wrong answers. Remember, numerical answer choices are always in ascending or descending order. Use that information to your advantage when using Backsolving. Start with either (B) or (D) first, because you’ll have a 40 percent chance of finding the correct answer based on your first round of calculations. If you don’t happen to pick the correct answer the first time, reason whether the number you started with was too large or too small. If you test choice (B) when the answer choices are in ascending order and (B) turns out to be too large, then (A) is the correct answer. If (B) is too small, then test choice (D). If (D) is too large, then (C) is the correct answer. If (D) is too small, then (E) is correct. The opposite would be true if the choices were in descending order. Backsolving allows you to find the correct answer without ever needing to test more than two of the answer choices.
Use Strategic Guessing
This is a good strategy if you can eliminate choices by applying number property rules or by estimating because gaps between answer choices are wide.
If some of the choices are out of the realm of possibility, eliminate them and move on.
Problem Solving Practice Set
Try the following Problem Solving questions using the Kaplan Method for Problem Solving. If you’re up to the challenge, time yourself; on Test Day, you’ll want to spend only about 2 minutes on each question.
1.
1. If r = 3s, s = 5t, t = 2u, and u ≠ 0, what is the value of ![]()
1. 30
2. 60
3. 150
4. 300
5. 600
2. In the diagram, l1 is parallel to l2. The measure of angle q is 40 degrees. What is the sum of the measures of the acute angles shown in the diagram?
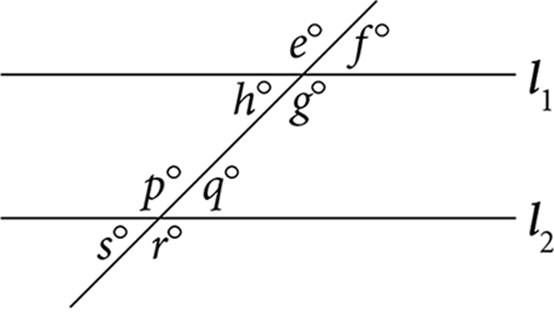
Note: Figure not drawn to scale.
Two rectangles with dimensions 2 meters by 4 meters overlap to form the figure above. All the angles shown measure 90°.
3. At Central Park Zoo, the ratio of sea lions to penguins is 4:11. If there are 84 more penguins than sea lions, how many sea lions are there?
1. 24
2. 36
3. 48
4. 72
5. 121
4. Which of the following are prime numbers between ![]() and
and ![]() Indicate all possible answers.
Indicate all possible answers.
1. 3
2. 4
3. 5
4. 7
5. 9
5. 
5. The figure above is made up of 3 squares. If the perimeter of the figure is 40 units, what is the area of the figure in square units?
1. 50
2. 75
3. 120
4. 150
5. 200
Answers and Explanations
PROBLEM SOLVING PRACTICE SET
1. E
The other variables all build upon u, so use the Picking Numbers strategy: pick a small number for u and find the values for r, s, and t. For instance, if u = 1, then t = 2u, so t = 2; s= 5t, so s = 10; and r = 3s, so r = 30.
So, ![]() The correct answer is (E).
The correct answer is (E).
2. 160In the diagram, there are four acute angles and four obtuse angles created when the parallel lines are cut by the transversal. If angle q has a measure of 40°, then angles s, h, and f each also has a measure of 40°. Therefore, the sum of their degree measures is 160.
3. CYou need to find the number of sea lions, and there are fewer sea lions than penguins, so starting small is a good idea. You can use the Backsolving strategy; start with choice (B), 36. If there are 36 sea lions, then there are 36 + 84 = 120 penguins, and the ratio of sea lions to penguins is ![]() This ratio is less than
This ratio is less than ![]() so your answer must be larger. If you try (D), there are 72 sea lions and there are 72 + 84 = 156 penguins, and the ratio of sea lions to penguins is
so your answer must be larger. If you try (D), there are 72 sea lions and there are 72 + 84 = 156 penguins, and the ratio of sea lions to penguins is ![]() Since this ratio is too large, the correct answer must be (C).
Since this ratio is too large, the correct answer must be (C).
4. A, C, D
You need to find a range of values between two improper fractions. First, change the improper fractions to mixed numbers: ![]() and
and ![]() Now, a prime number is a positive integer with only two distinct factors, 1 and itself. The prime numbers in the answer choices are 3, 5, and 7, and they are all between
Now, a prime number is a positive integer with only two distinct factors, 1 and itself. The prime numbers in the answer choices are 3, 5, and 7, and they are all between ![]() and
and ![]() So the correct answers are (A), (C), and (D).
So the correct answers are (A), (C), and (D).
5. BThere are 8 side lengths of the squares that make up the perimeter, which you are told is 40. So, each side of each square must be 5 units. The area of each square can be found by squaring one side, so each square has an area of 25 square units. Since there are three squares, the total area of the figure is 75 square units. The correct answer is (B).