CHEMISTRY THE CENTRAL SCIENCE
15 CHEMICAL EQUILIBRIUM
TRAFFIC ENTERING AND LEAVING a city.
WHAT'S AHEAD
15.1 THE CONCEPT OF EQUILIBRIUM
We begin by examining reversible reactions and the concept of equilibrium.
15.2 THE EQUILIBRIUM CONSTANT
We define the equilibrium constant based on rates of forward and reverse reactions, and learn how to write equilibrium-constant expressions for homogeneous reactions.
15.3 UNDERSTANDING AND WORKING WITH EQUILIBRIUM CONSTANTS
We learn to interpret the magnitude of an equilibrium constant and how its value depends on the way the corresponding chemical equation is expressed.
15.4 HETEROGENEOUS EQUILIBRIA
We then learn how to write equilibrium-constant expressions for heterogeneous reactions.
15.5 CALCULATING EQUILIBRIUM CONSTANTS
We see that the value of an equilibrium constant can be calculated from equilibrium concentrations of reactants and products.
15.6 APPLICATIONS OF EQUILIBRIUM CONSTANTS
We also see that equilibrium constants can be used to predict equilibrium concentrations of reactants and products and to determine the direction in which a reaction mixture must proceed to achieve equilibrium.
15.7 LE CHÂTELIER'S PRINCIPLE
We discuss Le Châtelier's principle, which predicts how a system at equilibrium responds to changes in concentration, volume, pressure, and temperature.
TO BE IN EQUILIBRIUM IS to be in a state of balance. A tug of war in which the two sides pull with equal force so that the rope does not move is an example of a static equilibrium, one in which an object is at rest. Equilibria can also be dynamic, as illustrated in the chapter-opening photograph, which shows cars traveling in both directions over a bridge that serves as the entry to a city. If the rate at which cars leave the city equals the rate at which they enter, the two opposing processes are in balance, and the net number of cars in the city is constant.
We have already encountered several instances of dynamic equilibrium. For example, the vapor above a liquid in a closed container is in equilibrium with the liquid phase 
(Section 11.5), which means that the rate at which molecules escape from the liquid into the gas phase equals the rate at which molecules in the gas phase become part of the liquid. Similarly, in a saturated sodium chloride solution in contact with undissolved sodium chloride, the solid is in equilibrium with the ions dispersed in water. (Section 13.2) The rate at which ions leave the solid surface equals the rate at which other ions leave the liquid and become part of the solid.
In this chapter we consider dynamic equilibria in chemical reactions. Chemical equilibrium occurs when opposing reactions proceed at equal rates: The rate at which the products form from the reactants equals the rate at which the reactants form from the products. As a result, concentrations cease to change, making the reaction appear to be stopped. Chemical equilibria are involved in many natural phenomena and play important roles in many industrial processes. In this and the next two chapters, we will explore chemical equilibrium in some detail. Later, inChapter 19, we will learn how to relate chemical equilibria to thermodynamics. Here we learn how to express the equilibrium state of a reaction in quantitative terms and study the factors that determine the relative concentrations of reactants and products in equilibrium mixtures.
15.1 THE CONCEPT OF EQUILIBRIUM
Let's examine a simple chemical reaction to see how it reaches an equilibrium state—a mixture of reactants and products whose concentrations no longer change with time. We begin with N2O4, a colorless substance that dissociates to form brown NO2. 
FIGURE 15.1 shows a sample of frozen N2O4 inside a sealed tube. The solid N2O4 vaporizes as it is warmed above its boiling point (21.2 °C), and the gas turns darker as the colorless N2O4 gas dissociates into brown NO2 gas. Eventually, even though there is still N2O4 in the tube, the color stops getting darker because the system reaches equilibrium. We are left with an equilibrium mixture of N2O4 and NO2 in which the concentrations of the gases no longer change as time passes. Because the reaction is in a closed system, where no gases can escape, equilibrium will eventually be reached.
GO FIGURE
How can you tell if you are at equilibrium?
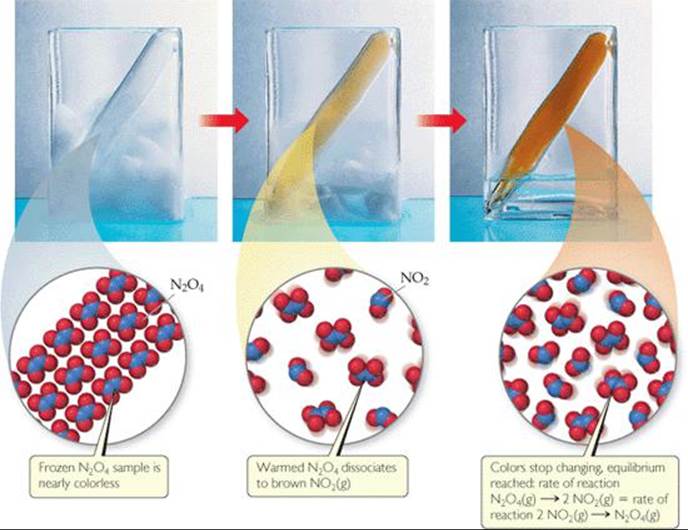
FIGURE 15.1 The equilibrium between NO2 and N2O4.
The equilibrium mixture results because the reaction is reversible: N2O4 can form NO2, and NO2 can form N2O4. This situation is represented by writing the equation for the reaction with two half arrows pointing in opposite directions: (Section 4.1)
We can analyze this equilibrium using our knowledge of kinetics. Let's call the decomposition of N2O4 the forward reaction and the formation of N2O4 the reverse reaction. In this case, both the forward reaction and the reverse reaction are elementary reactions. As we learned in Section 14.6, the rate laws for elementary reactions can be written from their chemical equations:
At equilibrium, the rate at which NO2 forms in the forward reaction equals the rate at which N2O4 forms in the reverse reaction:
Rearranging this equation gives
From Equation 15.5 we see that the quotient of two rate constants is another constant. We also see that, at equilibrium, the ratio of the concentration terms equals this same constant. (We consider this constant, called the equilibrium constant, in Section 15.2.) It makes no difference whether we start with N2O4 or with NO2, or even with some mixture of the two. At equilibrium, at a given temperature, the ratio equals a specific value. Thus, there is an important constraint on the proportions of N2O4 and NO2 at equilibrium.
Once equilibrium is established, the concentrations of N2O4 and NO2 no longer change, as shown in FIGURE 15.2 (a). However, the fact that the composition of the equilibrium mixture remains constant with time does not mean that N2O4 and NO2 stop reacting. On the contrary, the equilibrium is dynamic—which means some N2O4 is always converting to NO2 and some NO2 is always converting to N2O4. At equilibrium, however, the two processes occur at the same rate, as shown in Figure 15.2(b).
We learn several important lessons about equilibrium from this example:
• At equilibrium, the concentrations of reactants and products no longer change with time.
• For equilibrium to occur, neither reactants nor products can escape from the system.
• At equilibrium, a particular ratio of concentration terms equals a constant.
GO FIGURE
At equilibrium, are the concentrations of NO2 and N2O4 equal?
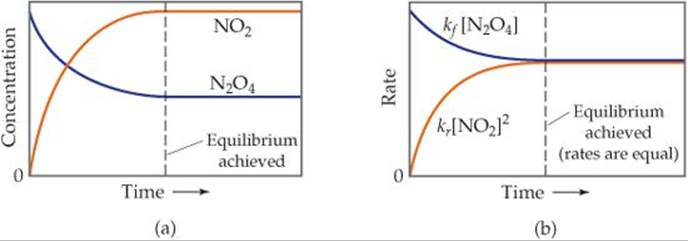
FIGURE 15.2 Achieving chemical equilibrium in the 
reaction. Equilibrium occurs when the rate of the forward reaction equals the rate of the reverse reaction.
GIVE IT SOME THOUGHT
a. Which quantities are equal in a dynamic equilibrium?
b. If the rate constant for the forward reaction in Equation 15.1 is larger than the rate constant for the reverse reaction, will the constant in Equation 15.5 be greater than 1 or smaller than 1?