CHEMISTRY THE CENTRAL SCIENCE
17 ADDITIONAL ASPECTS OF AQUEOUS EQUILIBRIA
17.4 SOLUBILITY EQUILIBRIA
The equilibria we have considered thus far in this chapter have involved acids and bases. Furthermore, they have been homogeneous; that is, all the species have been in the same phase. Through the rest of the chapter, we will consider the equilibria involved in the dissolution or precipitation of ionic compounds. These reactions are heterogeneous.
Dissolution and precipitation occur both within us and around us. Tooth enamel dissolves in acidic solutions, for example, causing tooth decay, and the precipitation of certain salts in our kidneys produces kidney stones. The waters of Earth contain salts dissolved as water passes over and through the ground. Precipitation of CaCO3 from groundwater is responsible for the formation of stalactites and stalagmites within limestone caves.
In our earlier discussion of precipitation reactions, we considered general rules for predicting the solubility of common salts in water. 
(Section 4.2) These rules give us a qualitative sense of whether a compound has a low or high solubility in water. By considering solubility equilibria, however, we can make quantitative predictions about solubility.
The Solubility-Product Constant, Ksp
Recall that a saturated solution is one in which the solution is in contact with undis-solved solute. (Section 13.2) Consider, for example, a saturated aqueous solution of BaSO4 in contact with solid BaSO4. Because the solid is an ionic compound, it is a strong electrolyte and yields Ba2+(aq) and SO42–(aq) ions when dissolved in water, readily establishing the equilibrium
As with any other equilibrium, the extent to which this dissolution reaction occurs is expressed by the magnitude of the equilibrium constant. Because this equilibrium equation describes the dissolution of a solid, the equilibrium constant indicates how soluble the solid is in water and is referred to as the solubility-product constant (or simply the solubility product). It is denoted Ksp, where sp stands for solubility product.
The equilibrium-constant expression for the equilibrium between a solid and an aqueous solution of its component ions is written according to the rules that apply to any other equilibrium-constant expression. Remember, however, that solids do not appear in the equilibrium-constant expressions for heterogeneous equilibrium. (Section 15.4) Thus, the solubility-product expression for BaSO4, which is based on Equation 17.15, is
In general, the solubility product Ksp of a compound equals the product of the concentration of the ions involved in the equilibrium, each raised to the power of its coefficient in the equilibrium equation. The coefficient for each ion in the equilibrium equation also equals its subscript in the compound's chemical formula.
The values of Ksp at 25 °C for many ionic solids are tabulated in Appendix D. The value of Ksp for BaSO4 is 1.1 × 10–10, a very small number indicating that only a very small amount of the solid dissolves in 25°C water.
SAMPLE EXERCISE 17.9 Writing Solubility-Product (Ksp) Expressions
Write the expression for the solubility-product constant for CaF2, and look up the corresponding Ksp value in Appendix D.
SOLUTION
Analyze We are asked to write an equilibrium-constant expression for the process by which CaF2 dissolves in water.
Plan We apply the general rules for writing an equilibrium-constant expression, excluding the solid reactant from the expression. We assume that the compound dissociates completely into its component ions:
Solve The expression for Ksp is
Appendix D gives 3.9 × 10–11 for this Ksp.
PRACTICE EXERCISE
Give the solubility-product-constant expressions and Ksp values (from Appendix D) for (a) barium carbonate, (b) silver sulfate.
Answers: (a) Ksp = [Ba2+][CO32–] = 5.0 × 10–9, (b) Ksp = [Ag+]2[SO42–] = 1.5 × 10–5
Solubility and Ksp
It is important to distinguish carefully between solubility and the solubility-product constant. The solubility of a substance is the quantity that dissolves to form a saturated solution. (Section 13.2) Solubility is often expressed as grams of solute per liter of solution (g/L). Molar solubilityis the number of moles of solute that dissolve in forming 1 L of saturated solution of the solute (mol/L). The solubility-product constant (Ksp) is the equilibrium constant for the equilibrium between an ionic solid and its saturated solution and is a unitless number. Thus, the magnitude of Kspis a measure of how much of the solid dissolves to form a saturated solution.
GIVE IT SOME THOUGHT
Without doing a calculation, predict which of these compounds has the greatest molar solubility in water: AgCl (Ksp = 1.8 × 10–10), AgBr (Ksp = 5.0 × 10–13), or AgI (Ksp = 8.3 × 10–17).
The solubility of a substance can change considerably in response to a number of factors. For example, the solubilities of hydroxide salts, like Mg(OH)2, are dependent upon the pH of the solution. The solubility is also affected by concentrations of other ions in solution, especially common ions. In other words, the numeric value of the solubility of a given solute can and does change as the other species in solution change. In contrast, the solubility-product constant, Ksp, has only one value for a given solute at any specific temperature.* 
FIGURE 17.16 summarizes the relationships among various expressions of solubility and Ksp.
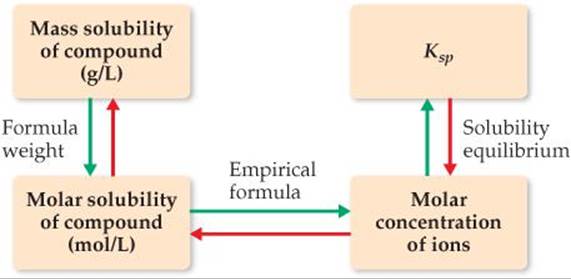
FIGURE 17.16 Procedure for converting between solubility and Ksp. Starting from the mass solubility, follow the green arrows to determine Ksp. Starting from Ksp, follow the red arrows to determine either molar solubility or mass solubility.
SAMPLE EXERCISE 17.10 Calculating Ksp from Solubility
Solid silver chromate is added to pure water at 25 °C, and some of the solid remains undis-solved. The mixture is stirred for several days to ensure that equilibrium is achieved between the undissolved Ag2CrO4(s) and the solution. Analysis of the equilibrated solution shows that its silver ion concentration is 1.3 ×10–4M. Assuming that Ag2CrO4 dissociates completely in water and that there are no other important equilibria involving Ag+ or CrO42– ions in the solution, calculate Ksp for this compound.
SOLUTION
Analyze We are given the equilibrium concentration of Ag+ in a saturated solution of Ag2CrO4 and asked to determine the value of Ksp for Ag2CrO4.
Plan The equilibrium equation and the expression for Ksp are
To calculate Ksp, we need the equilibrium concentrations of Ag+ and CrO42–. We know that at equilibrium [Ag+] = 1.3 × 10–4M. All the Ag+ and CrO42– ions in the solution come from the Ag2CrO4 that dissolves. Thus, we can use [Ag+] to calculate [CrO42–].
Solve From the chemical formula of silver chromate, we know that there must be 2 Ag+ ions in solution for each CrO42– ion in solution. Consequently, the concentration of CrO42– is half the concentration of Ag+:
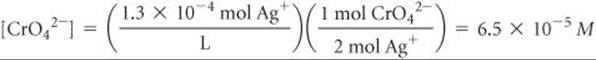
and Ksp is
Check We obtain a small value, as expected for a slightly soluble salt. Furthermore, the calculated value agrees well with the one given in Appendix D, 1.2 × 10–12.
PRACTICE EXERCISE
A saturated solution of Mg(OH)2 in contact with undissolved Mg(OH)2(s) is prepared at 25 °C. The pH of the solution is found to be 10.17. Assuming that Mg(OH)2 dissociates completely in water and that there are no other simultaneous equilibria involving the Mg2+ or OH– ions, calculateKsp for this compound.
Answer: 1.6 × 10–12
In principle, it is possible to use the Ksp value of a salt to calculate solubility under a variety of conditions. In practice, great care must be taken in doing so for the reasons indicated in “A Closer Look: Limitations of Solubility Products” at the end of this section. Agreement between the measured solubility and that calculated from Ksp is usually best for salts whose ions have low charges (1+ and 1–) and do not hydrolyze.
SAMPLE EXERCISE 17.11 Calculating Solubility from Ksp
The Ksp for CaF2 is 3.9 × 10–11 at 25 °C. Assuming that CaF2 dissociates completely upon dissolving and that there are no other important equilibria affecting its solubility, calculate the solubility of CaF2 in grams per liter.
SOLUTION
Analyze We are given Ksp for CaF2 and asked to determine solubility. Recall that the solubility of a substance is the quantity that can dissolve in solvent, whereas the solubility-product constant, Ksp, is an equilibrium constant.
Plan To go from Ksp to solubility, we follow the steps indicated by the red arrows in Figure 17.16. We first write the chemical equation for the dissolution and set up a table of initial and equilibrium concentrations. We then use the equilibrium-constant expression. In this case we know Ksp, and so we solve for the concentrations of the ions in solution. Once we know these concentrations, we use the formula weight to determine solubility in g/L.
Solve Assume that initially no salt has dissolved, and then allow x mol/L of CaF2 to dissociate completely when equilibrium is achieved:
The stoichiometry of the equilibrium dictates that 2x mol/L of F– are produced for each x mol/L of CaF2 that dissolve. We now use the expression for Ksp and substitute the equilibrium concentrations to solve for the value of x:
(Remember that 
. To calculate the cube root of a number, use the yx function on your calculator, with 
.) Thus, the molar solubility of CaF2 is 2.1 × 10–4 mol/L.
The mass of CaF2 that dissolves in water to form 1 L of solution is
Check We expect a small number for the solubility of a slightly soluble salt. If we reverse the calculation, we should be able to recalculate the solubility product: Ksp = (2.1 × 10–4)(4.2 × 10–4)2 = 3.7 × 10–11, close to the value given in the problem statement, 3.9 × 10–11.
Comment Because F– is the anion of a weak acid, you might expect hydrolysis of the ion to affect the solubility of CaF2. The basicity of F– is so small (Kb = 1.5 × 10–11), however, that the hydrolysis occurs to only a slight extent and does not significantly influence the solubility. The reported solubility is 0.017 g/L at 25 °C, in good agreement with our calculation.
PRACTICE EXERCISE
The Ksp for LaF3 is 2 × 10–19. What is the solubility of LaF3 in water in moles per liter?
Answer: 9 × 10–6 mol/L
A CLOSER LOOK
LIMITATIONS OF SOLUBILITY PRODUCTS
Ion concentrations calculated from Ksp values sometimes deviate appreciably from those found experimentally. In part, these deviations are due to electrostatic interactions between ions in solution, which can lead to ion pairs. (See Section 13.5, “A Closer Look: Colligative Properties of Electrolyte Solutions.”) These interactions increase in magnitude both as the concentrations of the ions increase and as their charges increase. The solubility calculated from Ksp tends to be low unless corrected to account for these interactions.
As an example of the effect of these interactions, consider CaCO3 (calcite), whose solubility product, Ksp = 4.5 × 10–9, gives a calculated solubility of 6.7 × 10–5 mol/L, and correcting for ionic interactions in the solution yields 7.3 × 10–5 mol/L. The reported solubility, however, is 1.4 × 10–4 mol/L, indicating that there must be additional factors involved.
Another common source of error in calculating ion concentrations from Ksp is ignoring other equilibria that occur simultaneously in the solution. It is possible, for example, that acid–base equilibria take place simultaneously with solubility equilibria. In particular, both basic anions and cations with high charge-to-size ratios undergo hydrolysis reactions that can measurably increase the solubilities of their salts. For example, CaCO3 contains the basic carbonate ion (Kb = 1.8 × 10–4), which hydrolyzes in water:
If we consider the effect of ion-ion interactions as well as simultaneous solubility and hydrolysis equilibria, we calculate a solubility of 1.4 × 10–4 mol/L, in agreement with the measured value.
Finally, we generally assume that ionic compounds dissociate completely when they dissolve, but this assumption is not always valid. When MgF2 dissolves, for example, it yields not only Mg2+ and F– ions but also MgF+ ions.