CHEMISTRY THE CENTRAL SCIENCE
17 ADDITIONAL ASPECTS OF AQUEOUS EQUILIBRIA
17.5 FACTORS THAT AFFECT SOLUBILITY
Solubility is affected by temperature and by the presence of other solutes. The presence of an acid, for example, can have a major influence on the solubility of a substance. In Section 17.4 we considered the dissolving of ionic compounds in pure water. In this section we examine three factors that affect the solubility of ionic compounds: (1) presence of common ions, (2) solution pH, and (3) presence of complexing agents. We will also examine the phenomenon of amphoterism, which is related to the effects of both pH and complexing agents.
Common-Ion Effect
The presence of either Ca2+(aq) or F–(aq) in a solution reduces the solubility of CaF2, shifting the solubility equilibrium to the left:

This reduction in solubility is another manifestation of the common-ion effect we looked at in Section 17.1. In general, the solubility of a slightly soluble salt is decreased by the presence of a second solute that furnishes a common ion, as ![]() FIGURE 17.17 shows for CaF2.
FIGURE 17.17 shows for CaF2.
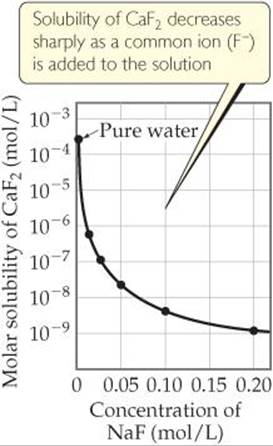
![]() FIGURE 17.17 Common-ion effect. Notice that the CaF2 solubility is on a logarithmic scale.
FIGURE 17.17 Common-ion effect. Notice that the CaF2 solubility is on a logarithmic scale.
SAMPLE EXERCISE 17.12 Calculating the Effect of a Common Ion on Solubility
Calculate the molar solubility of CaF2 at 25 °C in a solution that is (a) 0.010 M in Ca(NO3)2, (b) 0.010 M in NaF.
SOLUTION
Analyze We are asked to determine the solubility of CaF2 in the presence of two strong electrolytes, each containing an ion common to CaF2. In (a) the common ion is Ca2+, and NO3– is a spectator ion. In (b) the common ion is F–, and Na+ is a spectator ion.
Plan Because the slightly soluble compound is CaF2, we need to use Ksp for this compound, which Appendix D gives as 3.9 × 10–11. The value of Ksp is unchanged by the presence of additional solutes. Because of the common-ion effect, however, the solubility of the salt decreases in the presence of common ions. We use our standard equilibrium techniques of starting with the equation for CaF2 dissolution, setting up a table of initial and equilibrium concentrations, and using the Ksp expression to determine the concentration of the ion that comes only from CaF2.
Solve
(a) The initial concentration of Ca2+ is 0.010 M because of the dissolved Ca(NO3)2:

Substituting into the solubility-product expression gives
![]()
This would be a messy problem to solve exactly, but fortunately it is possible to simplify matters. Even without the common-ion effect, the solubility of CaF2 is very small (2.1 × 10–4M). Thus, we assume that the 0.010 M concentration of Ca2+ from Ca(NO3)2 is very much greater than the small additional concentration resulting from the solubility of CaF2; that is, x is much smaller than 0.010 M, and 0.010 + x ![]() 0.010. We then have
0.010. We then have
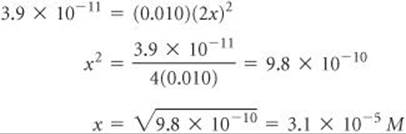
This very small value for x validates the simplifying assumption we made. Our calculation indicates that 3.1 × 10–5 mol of solid CaF2 dissolves per liter of 0.010 M Ca(NO3)2 solution.
(b) The common ion is F–, and at equilibrium we have
![]()
Assuming that 2x is much smaller than 0.010 M (that is, 0.010 + 2x ![]() 0.010), we have
0.010), we have
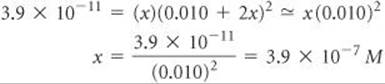
Thus, 3.9 × 10–7 mol of solid CaF2 should dissolve per liter of 0.010 M NaF solution.
Comment The molar solubility of CaF2 in water is 2.1 × 10–4M (Sample Exercise 17.11). By comparison, our calculations here give a CaF2 solubility of 3.1 × 10–5M in the presence of 0.010 M Ca2+ and 3.9 × 10–7M in the presence of 0.010 M F– ion. Thus, the addition of either Ca2+ or F– to a solution of CaF2 decreases the solubility. However, the effect of F– on the solubility is more pronounced than that of Ca2+ because [F–] appears to the second power in the Ksp expression for CaF2, whereas [Ca2+] appears to the first power.
PRACTICE EXERCISE
For manganese(II) hydroxide, Mn(OH)2, Ksp = 1.6 × 10–13. Calculate the molar solubility of Mn(OH)2 in a solution that contains 0.020 M NaOH.
Answer: 4.0 × 10–10M
Solubility and pH
The pH of a solution affects the solubility of any substance whose anion is basic. Consider Mg(OH)2, for which the solubility equilibrium is
![]()
A saturated solution of Mg(OH)2 has a calculated pH of 10.52 and its Mg2+ concentration is 1.7 × 10–4M. Now suppose that solid Mg(OH)2 is equilibrated with a solution buffered at pH 9.0. The pOH, therefore, is 5.0, so [OH–] = 1.0 × 10–5. Inserting this value for [OH–] into the solubility-product expression, we have
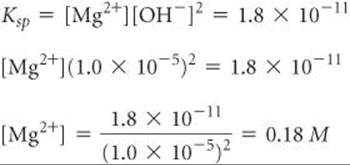
Thus, the Mg(OH)2 dissolves until [Mg2+] = 0.18 M. It is apparent that Mg(OH)2 is much more soluble in this solution.
 CHEMISTRY AND LIFE
CHEMISTRY AND LIFE
OCEAN ACIDIFICATION
Seawater is a weakly basic solution, with pH values typically between 8.0 and 8.3. This pH range is maintained through a carbonic acid buffer system similar to the one in blood (see Equation 17.10). Because the pH of seawater is higher than in blood (7.35–7.45), however, the second dissociation of carbonic acid cannot be neglected and CO32– becomes an important aqueous species.
The availability of carbonate ions plays an important role in shell formation for a number of marine organisms, including stony corals (![]() FIGURE 17.18). These organisms, which are referred to as marine calcifiers and play an important role in the food chains of nearly all oceanic ecosystems, depend on dissolved Ca2+ and CO32– ions to form their shells and exoskeletons. The relatively low solubilityproduct constant of CaCO3,
FIGURE 17.18). These organisms, which are referred to as marine calcifiers and play an important role in the food chains of nearly all oceanic ecosystems, depend on dissolved Ca2+ and CO32– ions to form their shells and exoskeletons. The relatively low solubilityproduct constant of CaCO3,
![]()
and the fact that the ocean contains saturated concentrations of Ca2+ and CO32– mean that CaCO3 is usually quite stable once formed. In fact, calcium carbonate skeletons of creatures that died millions of years ago are not uncommon in the fossil record.
Just as in our bodies, the carbonic acid buffer system can be perturbed by removing or adding CO2(g). The concentration of dissolved CO2 in the ocean is sensitive to changes in atmospheric CO2 levels. As discussed in Chapter 18, the atmospheric CO2 concentration has risen by approximately 30% over the past three centuries to the present level of 386 ppm. Human activity has played a prominent role in this increase. Scientists estimate that one-third to one-half of the CO2 emissions resulting from human activity have been absorbed by Earth's oceans. While this absorption helps mitigate the greenhouse gas effects of CO2, the extra CO2 in the ocean produces carbonic acid, which lowers the pH. Because CO32– is the conjugate base of the weak acid HCO3–, the carbonate ion readily combines with the hydrogen ion:
![]()
This consumption of carbonate ion shifts the dissolution equilibrium to the right, increasing the solubility of CaCO3. This can lead to partial dissolution of calcium carbonate shells and exoskeletons. If the amount of atmospheric CO2 continues to increase at the present rate, scientists estimate that seawater pH will fall to 7.9 sometime over the next 50 years. While this change might sound small, it has dramatic ramifications for oceanic ecosystems.
RELATED EXERCISES: 17.97

![]() FIGURE 17.18 Marine calcifiers. Many sea-dwelling organisms use CaCO3 for their shells and exoskeletons. Examples include stony coral, crustaceans, some phytoplankton, and echinoderms, such as sea urchins and starfish.
FIGURE 17.18 Marine calcifiers. Many sea-dwelling organisms use CaCO3 for their shells and exoskeletons. Examples include stony coral, crustaceans, some phytoplankton, and echinoderms, such as sea urchins and starfish.
If [OH–] were reduced further by making the solution even more acidic, the Mg2+ concentration would have to increase to maintain the equilibrium condition. Thus, a sample of Mg(OH)2(s) dissolves completely if sufficient acid is added, as we saw in Figure 4.9 (page 128).
The solubility of almost any ionic compound is affected if the solution is made sufficiently acidic or basic. The effects are noticeable, however, only when one (or both) ions in the compound are at least moderately acidic or basic. The metal hydroxides, such as Mg(OH)2, are examples of compounds containing a strongly basic ion, the hydroxide ion.
In general, the solubility of a compound containing a basic anion (that is, the anion of a weak acid) increases as the solution becomes more acidic. As we have seen, the solubility of Mg(OH)2 greatly increases as the acidity of the solution increases. The solubility of PbF2 increases as the solution becomes more acidic, too, because F– is a weak base (it is the conjugate base of the weak acid HF). As a result, the solubility equilibrium of PbF2 is shifted to the right as the concentration of F– is reduced by protonation to form HF. Thus, the solution process can be understood in terms of two consecutive reactions:
![]()
![]()
The equation for the overall process is
![]()
The processes responsible for the increase in solubility of PbF2 in acidic solution are illustrated in ![]() FIGURE 17.19 (a).
FIGURE 17.19 (a).
Other salts that contain basic anions, such as CO32–, PO43–, CN–, or S2–, behave similarly. These examples illustrate a general rule: The solubility of slightly soluble salts containing basic anions increases as [H+] increases (as pH is lowered). The more basic the anion, the more the solubility is influenced by pH. The solubility of salts with anions of negligible basicity (the anions of strong acids), such as Cl–, Br–, I– and NO3–, is unaffected by pH changes, as shown in Figure 17.19(b).
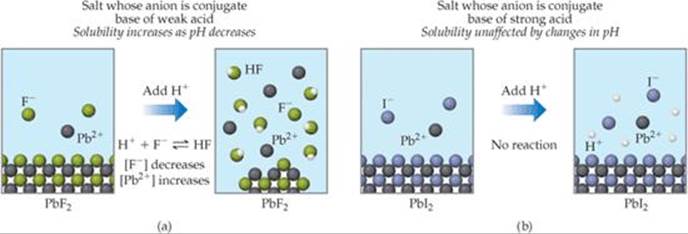
![]() FIGURE 17.19 Response of two ionic compounds to addition of a strong acid. (a) The solubility of PbF2 increases on addition of acid. (b) The solubility of PbI2 is not affected by addition of acid. The water molecules and the anion of the strong acid have been omitted for clarity.
FIGURE 17.19 Response of two ionic compounds to addition of a strong acid. (a) The solubility of PbF2 increases on addition of acid. (b) The solubility of PbI2 is not affected by addition of acid. The water molecules and the anion of the strong acid have been omitted for clarity.
SAMPLE EXERCISE 17.13 Predicting the Effect of Acid on Solubility
Which of these substances are more soluble in acidic solution than in basic solution: (a) Ni(OH)2(s), (b) CaCO3(s), (c) BaF2(s), (d) AgCl(s)?
SOLUTION
Analyze The problem lists four sparingly soluble salts, and we are asked to determine which are more soluble at low pH than at high pH.
Plan Ionic compounds that dissociate to produce a basic anion are more soluble in acid solution.
Solve
(a) Ni(OH)2(s) is more soluble in acidic solution because of the basicity of OH–; the H+reacts with the OH– ion, forming water:
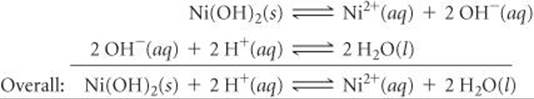
(b) Similarly, CaCO3(s) dissolves in acid solutions because CO32– is a basic anion:
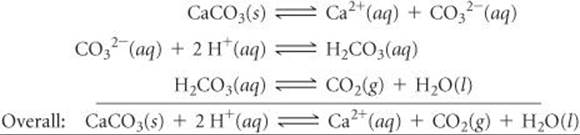
The reaction between CO32– and H+ occurs in steps, with HCO3– forming first and H2CO3 forming in appreciable amounts only when [H+] is sufficiently high.
(c) The solubility of BaF2 is enhanced by lowering the pH because F– is a basic anion:
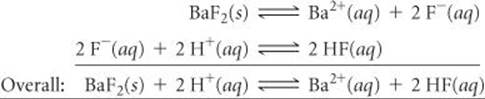
(d) The solubility of AgCl is unaffected by changes in pH because Cl– is the anion of a strong acid and therefore has negligible basicity.
PRACTICE EXERCISE
Write the net ionic equation for the reaction between an acid and (a) CuS, (b) Cu(N3)2.
Answers: ![]()
![]()
 CHEMISTRY AND LIFE
CHEMISTRY AND LIFE
TOOTH DECAY AND FLUORIDATION
Tooth enamel consists mainly of the mineral hydroxyapatite, Ca10(PO4)6(OH)2, the hardest substance in the body. Tooth cavities form when acids dissolve tooth enamel:
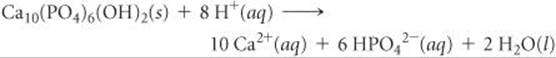
The Ca2+ and HPO42– ions diffuse out of the enamel and are washed away by saliva. The acids that attack the hydroxyapatite are formed by the action of bacteria on sugars and other carbohydrates present in the plaque adhering to the teeth.
Fluoride ion, which is added to municipal water systems and toothpastes, can react with hydroxy apatite to form fluoroapatite, Ca10(PO4)6F2. This mineral, in which F– has replaced OH–, is much more resistant to attack by acids because the fluoride ion is a mucl weaker Brønsted–Lowry base than the hydroxide ion.
The usual concentration of F– in municipal water systems is 1 mg/L (1 ppm). The compound added may be NaF or Na2SiF6. The silicon-fluorine anion reacts with water to release fluoride ions:
![]()
About 80% of all toothpastes now sold in the United States contain fluoride compounds, usually at the level of 0.1% fluoride by mass. The most common compounds in toothpastes are sodium fluoride (NaF), sodium monofluorophosphate (Na2PO3F), and stannous fluoride (SnF2).
RELATED EXERCISES: 17.98 and 17.116
Formation of Complex Ions
A characteristic property of metal ions is their ability to act as Lewis acids toward water molecules, which act as Lewis bases. ![]() (Section 16.11) Lewis bases other than water can also interact with metal ions, particularly transition-metal ions. Such interactions can dramatically affect the solubility of a metal salt. For example, AgCl (Ksp = 1.8 ×10–10) dissolves in the presence of aqueous ammonia because Ag+ interacts with the Lewis base NH3, as shown in
(Section 16.11) Lewis bases other than water can also interact with metal ions, particularly transition-metal ions. Such interactions can dramatically affect the solubility of a metal salt. For example, AgCl (Ksp = 1.8 ×10–10) dissolves in the presence of aqueous ammonia because Ag+ interacts with the Lewis base NH3, as shown in ![]() FIGURE 17.20. This process can be viewed as the sum of two reactions:
FIGURE 17.20. This process can be viewed as the sum of two reactions:
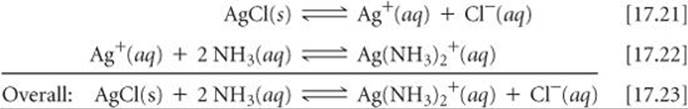
The presence of NH3 drives the reaction, the dissolution of AgCl, to the right as Ag+(aq) is consumed to form Ag(NH3)2+.
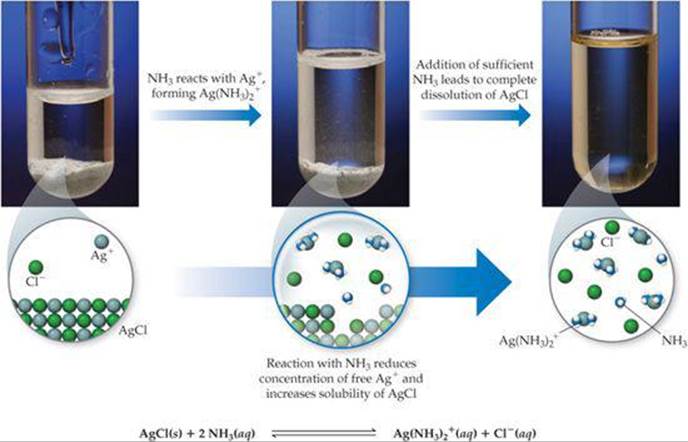
![]() FIGURE 17.20 Using concentrated NH3(aq) to dissolve AgCl(s), which has very low solubility in water.
FIGURE 17.20 Using concentrated NH3(aq) to dissolve AgCl(s), which has very low solubility in water.
For a Lewis base such as NH3 to increase the solubility of a metal salt, the base must be able to interact more strongly with the metal ion than water does. In other words, the NH3 must displace solvating H2O molecules ![]() (Sections 13.1 and 16.11) in order to form Ag(NH3)2+:
(Sections 13.1 and 16.11) in order to form Ag(NH3)2+:
![]()
TABLE 17.1 • Formation Constants for Some Metal Complex Ions in Water at 25 °C
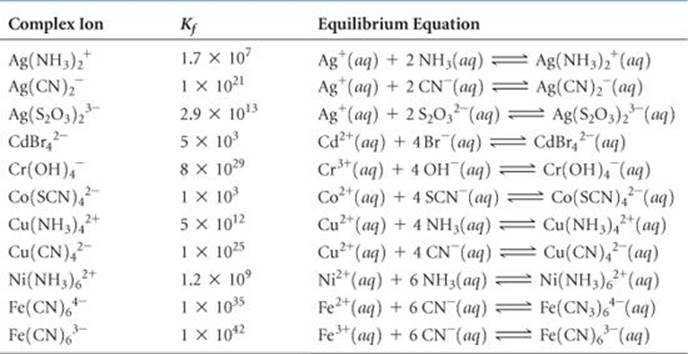
An assembly of a metal ion and the Lewis bases bonded to it, such as Ag(NH3)2+, is called a complex ion. The stability of a complex ion in aqueous solution can be judged by the size of the equilibrium constant for its formation from the hydrated metal ion. For example, the equilibrium constant for Equation 17.24 is
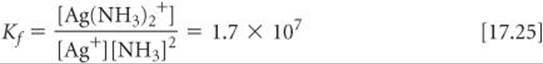
Note that the equilibrium constant for this kind of reaction is called a formation constant, Kf. The formation constants for several complex ions are listed in ![]() TABLE 17.1.
TABLE 17.1.
SAMPLE EXERCISE 17.14 Evaluating an Equilibrium Involving a Complex Ion
Calculate the concentration of Ag+ present in solution at equilibrium when concentrated ammonia is added to a 0.010 M solution of AgNO3 to give an equilibrium concentration of [NH3] = 0.20 M. Neglect the small volume change that occurs when NH3 is added.
SOLUTION
Analyze Addition of NH3(aq) to Ag+(aq) forms Ag(NH3)2+, as shown in Equation 17.22. We are asked to determine what concentration of Ag+(aq) remains uncombined when the NH3 concentration is brought to 0.20 M in a solution originally 0.010 M in AgNO3.
Plan We assume that the AgNO3 is completely dissociated, giving 0.010 M Ag+. Because Kf for the formation of Ag(NH3)2+ is quite large, we assume that essentially all the Ag+ is converted to Ag(NH3)2+ and approach the problem as though we are concerned with the dissociation of Ag(NH3)2+ rather than its formation. To facilitate this approach, we need to reverse Equation 17.22 and make the corresponding change to the equilibrium constant:
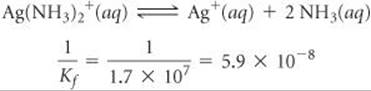
Solve If [Ag+] is 0.010 M initially, [Ag(NH3)2+] will be 0.010 M following addition of the NH3. We construct a table to solve this equilibrium problem. Note that the NH3 concentration given in the problem is an equilibrium concentration rather than an initial concentration.

Because [Ag+] is very small, we can ignore x, so that 0.010 – x ![]() 0.010 M. Substituting these values into the equilibrium-constant expression for the dissociation of Ag(NH3)2+, we obtain
0.010 M. Substituting these values into the equilibrium-constant expression for the dissociation of Ag(NH3)2+, we obtain
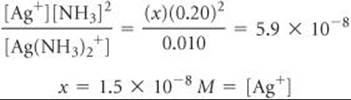
Formation of the Ag(NH3)2+ complex drastically reduces the concentration of free Ag+ ion in solution.
PRACTICE EXERCISE
Calculate [Cr3+] in equilibrium with Cr(OH)4– when 0.010 mol of Cr(NO3)3 is dissolved in 1 L of solution buffered at pH 10.0.
Answer: 1 × 10–16M
The general rule is that the solubility of metal salts increases in the presence of suitable Lewis bases, such as NH3, CN–, or OH–, provided the metal forms a complex with the base. The ability of metal ions to form complexes is an extremely important aspect of their chemistry.
Amphoterism
Some metal oxides and hydroxides that are relatively insoluble in water dissolve in strongly acidic and strongly basic solutions. These substances, called amphoteric oxides and amphoteric hydroxides,* are soluble in strong acids and bases because they themselves are capable of behaving as either an acid or base. Examples of amphoteric substances include the oxides and hydroxides of Al3+, Cr3+, Zn2+, and Sn2+.
Like other metal oxides and hydroxides, amphoteric species dissolve in acidic solutions because their anions, O2– or OH–, react with acids. What makes amphoteric oxides and hydroxides special, though, is that they also dissolve in strongly basic solutions. This behavior results from the formation of complex anions containing several (typically four) hydroxides bound to the metal ion (![]() FIGURE 17.21):
FIGURE 17.21):
![]()
The extent to which an insoluble metal hydroxide reacts with either acid or base varies with the particular metal ion involved. Many metal hydroxides—such as Ca(OH)2, Fe(OH)2, and Fe(OH)3—are capable of dissolving in acidic solution but do not react with excess base. These hydroxides are not amphoteric.
The purification of aluminum ore in the manufacture of aluminum metal provides an interesting application of amphoterism. As we have seen, Al(OH)3 is amphoteric, whereas Fe(OH)3 is not. Aluminum occurs in large quantities as the ore bauxite, which is essentially hydrated Al2O3contaminated with Fe2O3. When bauxite is added to a strongly basic solution, the Al2O3 dissolves because the aluminum forms complex ions, such as Al(OH)4–. The Fe2O3 impurity, however, is not amphoteric and remains as a solid. The solution is filtered, getting rid of the iron impurity. Aluminum hydroxide is then precipitated by addition of acid. The purified hydroxide receives further treatment and eventually yields aluminum metal.
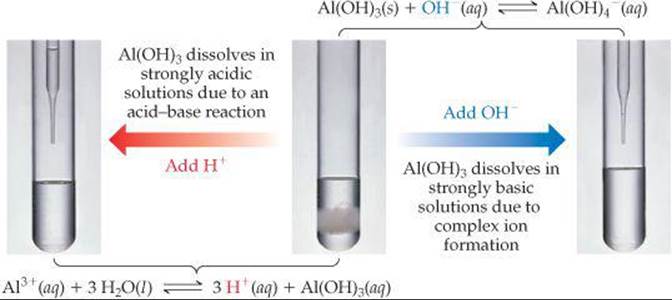
![]() FIGURE 17.21 Amphoterism. Some metal oxides and hydroxides, such as Al(OH)3, are amphoteric, which means they dissolve in both strongly acidic and strongly basic solutions.
FIGURE 17.21 Amphoterism. Some metal oxides and hydroxides, such as Al(OH)3, are amphoteric, which means they dissolve in both strongly acidic and strongly basic solutions.
![]() GIVE IT SOME THOUGHT
GIVE IT SOME THOUGHT
What is the difference between an amphoteric substance and an amphiprotic substance?