Introductory Chemistry: A Foundation - Zumdahl S.S., DeCoste D.J. 2019

Energy
Measuring Energy Changes

Objective

· To understand how heat is measured.

Earlier in this chapter we saw that when we heat a substance to a higher temperature, we increase the motions of the components of the substance—that is, we increase the thermal energy of the substance. Different materials respond differently to being heated. To explore this idea we need to introduce the common units of energy: the calorie and the joule (pronounced “jewel”).

In the metric system the calorie is defined as the amount of energy (heat) required to raise the temperature of one gram of water by one Celsius degree. The “calorie” with which you are probably familiar is used to measure the energy content of food and is actually a kilocalorie ( calories), written with a capital (Calorie) to distinguish it from the calorie used in chemistry. The joule (an SI unit) can be most conveniently defined in terms of the calorie:

or using the normal abbreviations

You need to be able to convert between calories and joules. We will consider that conversion process in Example 10.1.

Interactive Example 10.1. Converting Calories to Joules

Express cal of energy in units of joules.

Solution

By definition , so the conversion factor needed is , and the result is

Note that the in the denominator is an exact number by definition and so does not limit the number of significant figures.

Self-Check: Exercise 10.1

· How many calories of energy correspond to J?

See Problems 10.25, 10.26, 10.27, 10.28, 10.29, and 10.30.

Now think about heating a substance from one temperature to another. How does the amount of substance heated affect the energy required? In g of water there are twice as many molecules as in g of water. It takes twice as much energy to change the temperature of g of water by because we must change the motions of twice as many molecules in a -g sample as in a -g sample. Also, as we would expect, it takes twice as much energy to raise the temperature of a given sample of water by degrees as it does to raise the temperature by degree.

Interactive Example 10.2. Calculating Energy Requirements

Determine the amount of energy (heat) in joules required to raise the temperature of g water from to .

Solution

Where Are We Going?

We want to determine the amount of energy (heat in joules) needed to increase the temperature of g water from to .

What Do We Know?

· The mass of water is g, and the temperature is increased from to .

What Do We Need to Know?

· The amount of heat needed to raise g water by . From the text we see that J of energy is required.

How Do We Get There?

In solving any kind of problem, it is often useful to draw a diagram that represents the situation. In this case, we have g of water that is to be heated from to .

Our task is to determine how much energy is required to accomplish this change.

From the discussion in the text, we know that J of energy is required to raise the temperature of one gram of water by one Celsius degree.

Because in our case we have g of water instead of g, it will take J to raise the temperature by one degree.

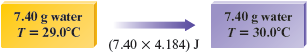
However, we want to raise the temperature of our sample of water by more than . In fact, the temperature change required is from to . This is a change of . Thus we will have to supply times the energy necessary to raise the temperature of g of water by .

This calculation is summarized as follows:

We have shown that J of energy (as heat) is required to raise the temperature of g of water from to . Note that because J of energy is required to heat g of water by , the units are (joules per gram per Celsius degree).

Reality Check The units (J) are correct, and the answer is reported to the correct number of significant figures (three).

Self-Check: Exercise 10.2

· Calculate the joules of energy required to heat g of water from to .

See Problems 10.31, 10.32, 10.33, 10.34, 10.35, and 10.36.

Chemistry in Focus Coffee: Hot and Quick(lime)

Convenience and speed are the watchwords of our modern society. One new product that fits these requirements is a container of coffee that heats itself with no batteries needed. Consumers can now buy a -ounce container of Wolfgang Puck gourmet latte that heats itself to in minutes and stays hot for minutes. What kind of chemical magic makes this happen? Pushing a button on the bottom of the container. This action allows water to mix with calcium oxide, or quicklime (see accompanying figure). The resulting reaction

releases enough energy as heat to bring the coffee to a pleasant drinking temperature.

Other companies are experimenting with similar technology to heat liquids such as tea, hot chocolate, and soup.

A different reaction is now being used to heat MREs (meals ready-to-eat) for soldiers on the battlefield. In this case the energy to heat the meals is furnished by mixing magnesium iron oxide with water to produce an exothermic reaction.

Clearly, chemistry is “hot stuff.”

See Problem 10.36

So far we have seen that the energy (heat) required to change the temperature of a substance depends on

1. The amount of substance being heated (number of grams)

2. The temperature change (number of degrees)

There is, however, another important factor: the identity of the substance.

Different substances respond differently to being heated. We have seen that J of energy raises the temperature of g of water by . In contrast, this same amount of energy applied to g of gold raises its temperature by approximately The point is that some substances require relatively large amounts of energy to change their temperatures, whereas others require relatively little. Chemists describe this difference by saying that substances have different heat capacities. The amount of energy required to change the temperature of one gram of a substance by one Celsius degree is called its specific heat capacity or, more commonly, its specific heat. The specific heat capacities for several substances are listed in Table 10.1. You can see from the table that the specific heat capacity for water is very high compared to those of the other substances listed. This is why lakes and seas are much slower to respond to cooling or heating than are the surrounding land masses.

Table 10.1. The Specific Heat Capacities of Some Common Substances

Chemistry in Focus Nature Has Hot Plants

The voodoo lily (titan arum) is a beautiful and seductive plant. The exotic-looking lily features an elaborate reproductive mechanism—a purple spike that can reach nearly feet in length and is cloaked by a hoodlike leaf. But approach to the plant reveals bad news—it smells terrible!

Despite its antisocial odor, this putrid plant has fascinated biologists for many years because of its ability to generate heat. At the peak of its metabolic activity, the plant’s blossom can be as much as above its surrounding temperature. To generate this much heat, the metabolic rate of the plant must be close to that of a flying hummingbird!

What’s the purpose of this intense heat production? For a plant faced with limited food supplies in the very competitive tropical climate where it grows, heat production seems like a great waste of energy. The answer to this mystery is that the voodoo lily is pollinated mainly by carrion-loving insects. Thus the lily prepares a malodorous mixture of chemicals characteristic of rotting meat, which it then “cooks” off into the surrounding air to attract flesh-feeding beetles and flies. Then, once the insects enter the pollination chamber, the high temperatures there (as high as ) cause the insects to remain very active to better carry out their pollination duties.

The voodoo lily is only one of many thermogenic (heat-producing) plants. These plants are of special interest to biologists because they provide opportunities to study metabolic reactions that are quite subtle in “normal” plants.

See Problem 10.37

Interactive Example 10.3. Calculations Involving Specific Heat Capacity

a. What quantity of energy (in joules) is required to heat a piece of iron weighing g from to ?

b. What is the answer in calories?

Solution

Where Are We Going?

We want to determine the amount of energy (units of joules and calories) to increase the temperature of g of iron from to .

What Do We Know?

· The mass of iron is g, and the temperature is increased from to .

What Do We Need to Know?

· We need the specific heat capacity of iron and the conversion factor between joules and calories.

How Do We Get There?

a. It is helpful to draw the following diagram to represent the problem.

From Table 10.1 we see that the specific heat capacity of iron is . That is, it takes J to raise the temperature of a -g piece of iron by .

In this case our sample is g, so J is required for each degree of temperature increase.

Because the temperature increase is , the total amount of energy required is

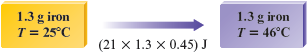
Note that the final units are joules, as they should be.

b. To calculate this energy in calories, we can use the definition to construct the appropriate conversion factor. We want to change from joules to calories, so cal must be in the numerator and J in the denominator, where it cancels:

Remember that in this case is an exact number by definition and therefore does not limit the number of significant figures (the number is limiting here).

Reality Check The units (joules and calories) are correct, and the answer is reported to the correct number of significant figures (two).

Self-Check: Exercise 10.3

· A -g sample of solid gold is heated from to . How much energy (in joules and calories) is required?

See Problems 10.31, 10.32, 10.33, 10.34, 10.35, and 10.36.

Note that in Example 10.3, to calculate the energy (heat) required, we took the product of the specific heat capacity, the sample size in grams, and the change in temperature in Celsius degrees.

We can represent this by the following equation:

where

Chemistry in Focus Firewalking: Magic or Science?

For millennia people have been amazed at the ability of Eastern mystics to walk across beds of glowing coals without any apparent discomfort. Even in the United States, thousands of people have performed feats of firewalking as part of motivational seminars. How can this be possible? Do firewalkers have supernatural powers?

Actually, there are good scientific explanations of why firewalking is possible. First, human tissue is mainly composed of water, which has a relatively large specific heat capacity. This means that a large amount of energy must be transferred from the coals to change the temperature of the feet significantly. During the brief contact between feet and coals involved in firewalking, there is relatively little time for energy flow, so the feet do not reach a high enough temperature to cause damage.

Also, although the surface of the coals has a very high temperature, the red-hot layer is very thin. Therefore, the quantity of energy available to heat the feet is smaller than might be expected.

Thus, although firewalking is impressive, there are several scientific reasons why anyone with the proper training should be able to do it on a properly prepared bed of coals. (Don’t try this on your own!)

See Problem 10.38

This equation always applies when a substance is being heated (or cooled) and no change of state occurs. Before you begin to use this equation, however, make sure you understand what it means.

Example 10.4. Specific Heat Capacity Calculations: Using the Equation

A -g sample of a metal that has the appearance of gold requires J of energy to change its temperature from to . Is the metal pure gold?

Solution

Where Are We Going?

We want to determine if a metal is gold.

What Do We Know?

· The mass of metal is g, and J of energy is required to increase the temperature from to .

What Do We Need to Know?

· We need the specific heat capacity of gold.

How Do We Get There?

We can represent the data given in this problem by the following diagram:

Using the data given, we can calculate the value of the specific heat capacity for the metal and compare this value to the one for gold given in Table 10.1. We know that

or, pictorially,

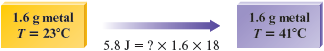
When we divide both sides of the equation

by , we get

Thus, using the data given, we can calculate the value of . In this case,

Thus

From Table 10.1, the specific heat capacity for gold is . Thus the metal must not be pure gold.

Self-Check: Exercise 10.4

· A -g sample of pure metal requires J of energy to change its temperature from to . What is this metal? (Use Table 10.1.)

See Problems 10.31, 10.32, 10.33, 10.34, 10.35, and 10.36.