Process Technology: An Introduction - Haan A.B. 2015

17 Hydrodynamic aspects of scale-up
17.3 Scale-up methodology for mixing processes

A major problem in agitator design is to scale up from a laboratory or pilot plant agitator to a full-scale unit. For many problems adequate mathematical models and/or scale-up correlations are not available. Various methods of scale-up have been proposed for these situations, all based on geometric similarity between the laboratory and plant equipment. It is not always possible, however, to have the large and small vessels geometrically similar. Furthermore, even if geometric similarity is obtainable, dynamic similarity and kinematic similarity are not, so that the results of the scaleup are not always fully predictable. Important techniques to assist an engineer in the scale-up of mixing operations include dimensional, similarity, and regime analysis.

17.3.1 Dimensional, similarity, and regime analysis

Dimensional analysis is a mathematical tool for scale-up or scale-down of physical and chemical process equipment. It proceeds from the general principle that physical laws must be independent of the units of measurement used to express them. If one quantity is related to a group of other quantities, the quantities comprising the group must be related in such a manner that the net units or dimensions of the group are the same as those of the dependent quantity. Division can then form a dimensionless group immediately. The final result is a complete set of dimensionless quantities that describe the physical process and that indicates the conditions for which this process behaves “similarly” in the model and on the desired scale. The most important dimensionless number in chemical engineering is the Reynolds number, which is easily shown to be dimensionless:

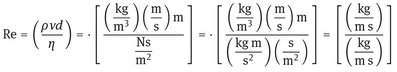
= [—]. (17.3)

The most important strength of dimensional analysis lies in its ability to reduce the number of parameters required to describe complex problems and provide deeper insight into the physical nature of a process. It can even handle lack of geometrical symmetry by using ratios of important dimensions as additional dimensionless numbers. This limits the number of work that needs to be done to handle situations in which the governing equations are not known. However, the weakness of dimensional analysis lies in the need to know, in advance, which variables must be included and which can be ignored. This reflects the fact that dimensional analysis is not capable of describing the functional relationship among the dimensionless groups and the extrapolation of their empirical relationship outside the range covered by the original data. Achieving the simplest most meaningful relationship and to judge how it might best be extrapolated still relies heavily on previous experience and the physical insight of the engineer.

After the dimensionless numbers are obtained, one has to make sure that these numbers do not change when scaling up. Two processes of different scale are considered similar if they take place under geometrically similar conditions and all dimensionless quantities describing the process have the same numerical value. This is the general idea behind similarity analysis and ensures that the full-scale process behaves similar to the experiments performed. However, in practice it always appears impossible to keep all dimensionless numbers and geometric ratios constant during scale-up, because they depend differently on the variables, or due to mechanical constrains. In such situations a compromise needs to be found, and another technique is needed to solve these problems: regime analysis. This is a formalized theory to predict which dimensionless numbers are (more) important, and thus have to remain constant, and which are not (less) important.

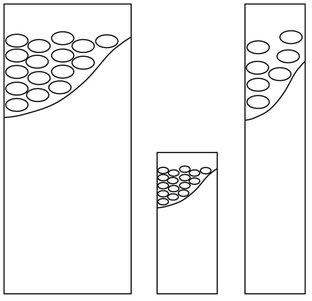
Fig. 17.12: Example of a nongeometrical similarity: the full-scale model is at the left, the geometrically similar small-scale model in the middle, and the setup actually used at the right.

Regime analysis deals with determining the rate-limiting step in the process. Because dimensionless numbers often represent ratios of transport mechanisms, process changes may occur when a dimensionless number has a value around one. Regime analysis investigates which dimensionless numbers are most important for a certain regime (i.e. have a value between 0.1 and 10). The advantage of knowing the regime is that one only has to control the dimensionless groups belonging to that regime. In such a case only partial similarity can be obtained: the important dimensionless numbers are kept constant, and the others are allowed to vary. A phenomenon that may occur in practice is that another regime is rate limiting for a small-scale problem rather than for the large-scale situation. In such cases it might be necessary to change the circumstances for the small-scale situation such that the same regime is limiting at both scales, or to release the requirement of geometrical similarity. An example is a tube reactor with a mixed thermal and chemical regime. The problem is that the specific surface decreases during pure geometrical scale-up, and the ratio of heat transfer and heat production changes. This can be compensated for by using so-called elements at small-scale as illustrated by Fig. 17.12. The small-scale model has the same height but smaller diameter as the larger scale prototype and the dimension of packing elements and catalyst particles is not decreased, to ensure equal rate-limiting steps in both setups.

Tab. 17.1: Important geometrical ratios for a stirred tank and their value for a the standard mixing vessel shown in Fig. 17.13.

17.3.2 Important dimensionless numbers for mixing processes

The most obvious dimensionless numbers that are used in scale modification of mixing processes are geometrical ratios (for example, height of the tank divided by the diameter) in case of geometrical scale-up. Most of the important values have been investigated thoroughly, and for most situations optimal ratios have been found, which can be applied in other cases as well. These are summarized in Tab. 17.1. Other important ratios are flow number, circulation time, power density, and the power number. The flow number φ represents the ratio between the flow supplied and the flow from the impeller:

(17.4)

The circulation time is the ratio of the volume of the tank divided by the flow from the impeller. It indicates how long it takes for the impeller to move a volume of liquid equal to the volume of the tank and thus gives an indication for the mixing intensity. In a process that is controlled by micromixing, it is important to keep the power density ε constant. It represents the amount of energy applied for mixing per unit of mass of the mixture:

(17.5)

Finally the power number represents the power required to drive the impeller and is often given as a correlation of dimensionless numbers to allow determination of the required power when scaling up or down.

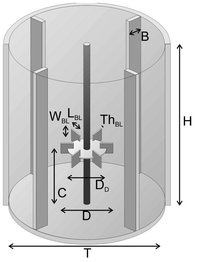
Fig. 17.13: Standard mixing vessel.