High School Algebra I Unlocked (2016)

Lesson 7.2. Intervals and Interval Notation

Often the domain and range of a function will be expressed in interval notation. An interval is a set of real numbers between, and at times including, two numbers. Consider the following examples that express the domain of a function using interval notation:

The use of brackets ([ ]) in interval notation indicates that the value of the endpoint is included in the interval; graphically, the endpoints will be filled circles. Conversely, the use of parentheses (( )) in interval notation indicates that the value of the endpoint is not included in the interval; graphically, the endpoints will be unfilled circles.

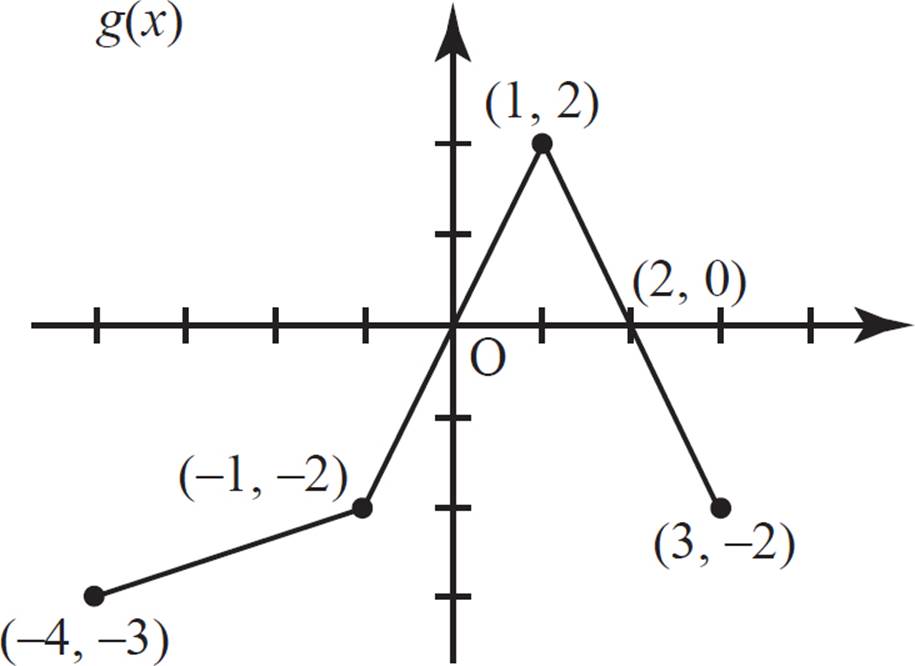
Consider the graph of g(x). In this function, the least x-value is −4, the greatest x-value is 3, and all of the points on the graph are depicted as filled circles. Therefore, the domain of g(x) includes all real numbers between −4 and 3, including both −4 and 3, and is written in interval notation as [−4, 3]. You can also use interval notation to express the range, or all possible y-values, of a function. Let’s try a couple questions that focus on interval notation.

EXAMPLE

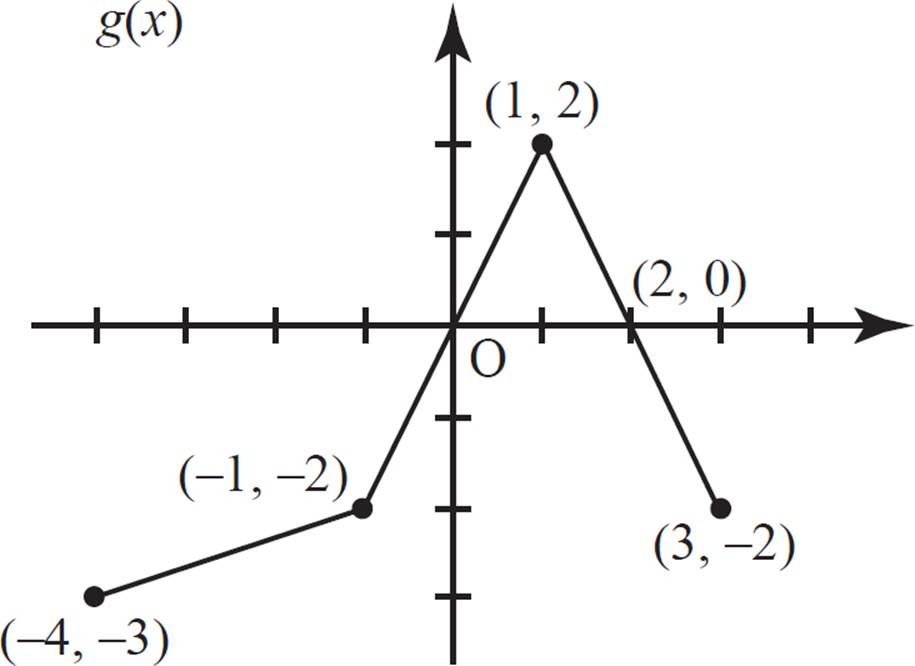
Express the range of g(x) in interval notation.

In the graph of g(x), the lowest y−value is −3, which occurs at point (−4, −3), and the greatest y-value is 2, which occurs at point (1, 2). Since both of these points are filled-in circles, and therefore included in the range, the function g(x) has a range of [−3, 2].

EXAMPLE

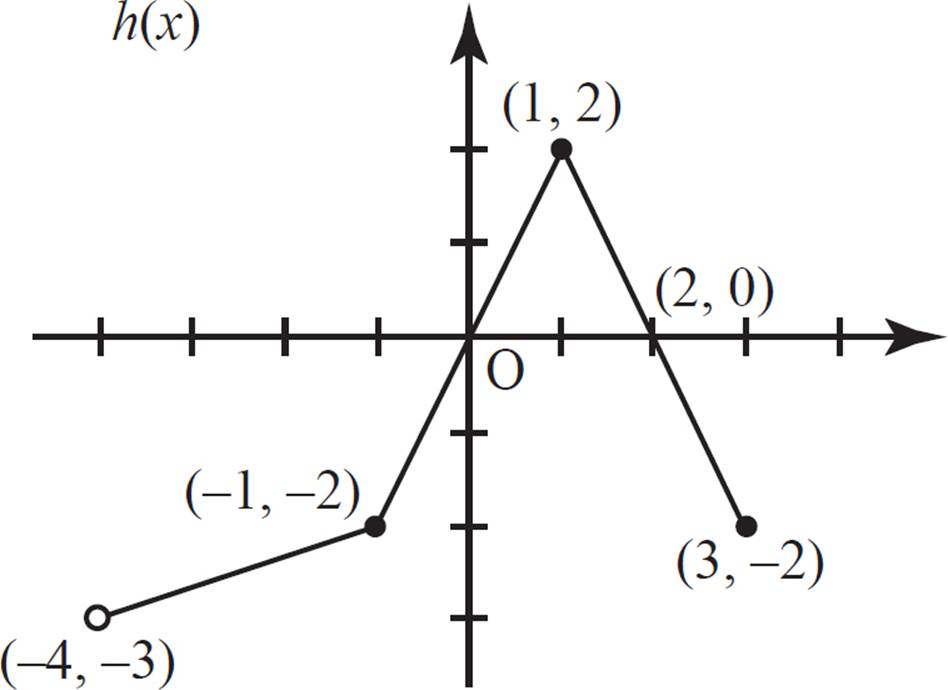
Express the domain and range of h(x) in interval notation.

Since h(x) has x-values that range from −4 to 3, but point (−4, −3) has an unfilled endpoint, the domain of h(x) is (−4, 3]. Similarly, h(x) has y-values that range from −3 to 2, but point (−4, −3) has an unfilled endpoint, signifying that the range of h(x) is (−3, 2].

Thus, the function h(x) has a domain of (−4, 3] and a range of (−3, 2].

But what if the function is discontinuous at various points? How would it be represented in interval notation? To express a domain that is true over multiple intervals, you use the union symbol: ∪. To understand how this works, look at the graph below.

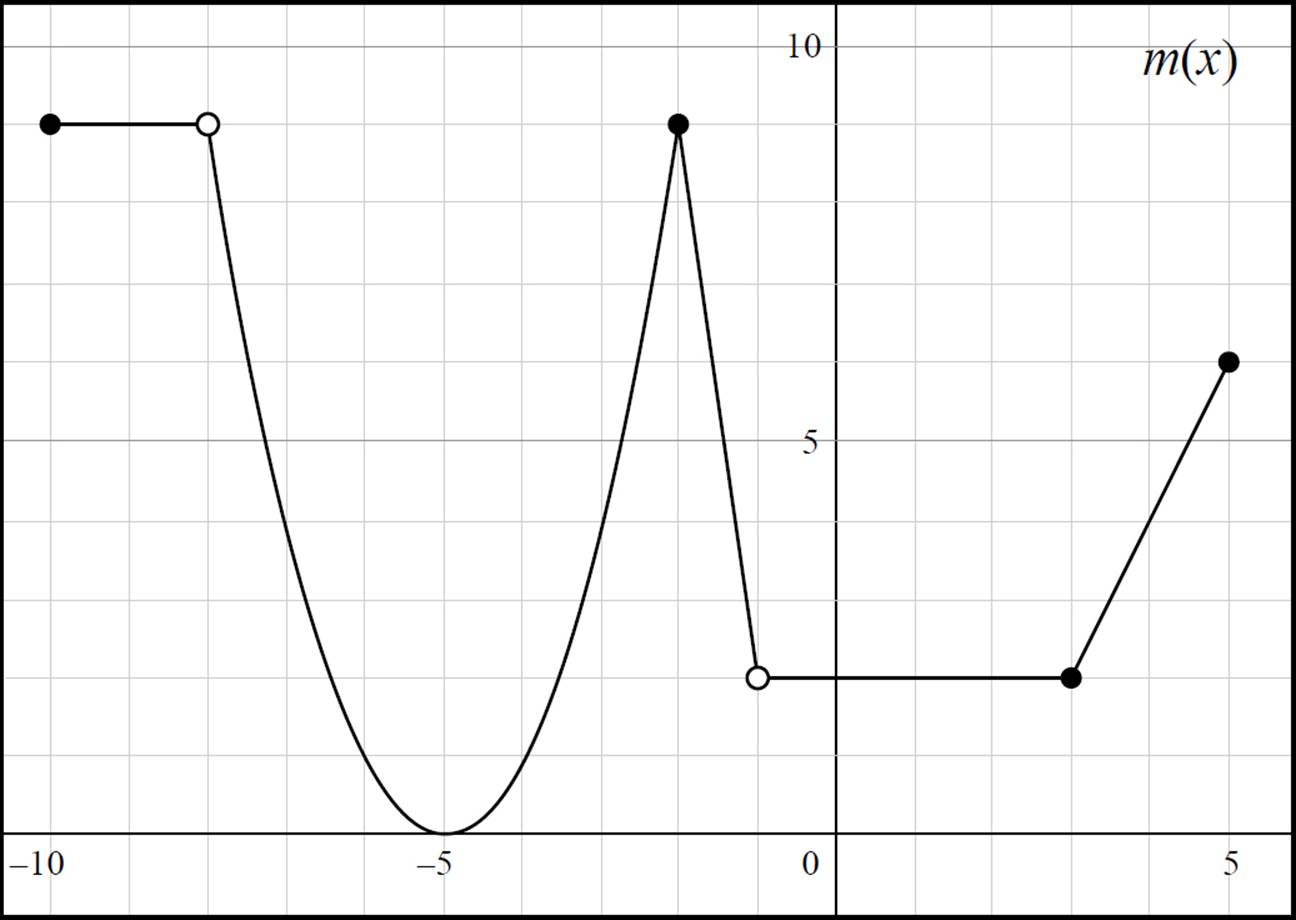
Let’s use this graph to determine the domain and range of m(x), and state them in interval notation. Based on the graph, you can determine that m(x) is has x-values that range from x = −10 to x = −8, where x = −8 is not included in the domain. Therefore, you would express this interval as [−10, −8). Then find the next interval, which exists from x = −8 to x = −2; again, x = −8 is not included. Thus, this interval is expressed as (−8, −2]. Repeat the process for the next interval, which goes from x = −2 to x = −1, where −1 is not included. This interval is expressed as [−2, −1). Finally, find the last interval, which goes from x = −1 to x = 5, where x = −1 is not included. This interval is expressed as (−1, 5].

Now you need to join all of the intervals together with the union symbol to express the domain of m(x). Therefore, the domain of m(x) is [−10, −8) ∪ (−8, −2] ∪ [−2, −1) ∪ (−1, 5]. Since −2 is included in both the intervals (−8, −2] and [−2, −1), the domain can also be expressed as [−10, −8) ∪ (−8, −1) ∪ (−1, 5].

But what if the function goes on forever? Is that even possible? Of course it is! Consider the linear function ƒ(x) = x + 6:

Unlike the previous graphs, g(x) and h(x), the graph of ƒ(x) doesn’t have any endpoints. No worries—you can still define the domain and range of ƒ(x) using the infinity sign (∞) in your interval notation to represent intervals that extend indefinitely in one or both directions.

Since the function ƒ(x) = x + 6 extends infinitely in both directions, across all x- and y-values, both the domain and range of ƒ(x) would be represented by the interval (−∞, ∞).

Notice that the infinity
sign is not associated with
brackets. Since the infinity
symbol does not represent
a specific number, it will
always be accompanied
by a parenthesis.