High School Algebra I Unlocked (2016)
Chapter 10. Other Functions
GOALS
By the end of this chapter, you will be able to:
•Identify absolute value, step, and piecewise functions
•Graph and manipulate absolute value, step, and piecewise functions
•Determine whether a function is continuous or discontinuous
•Determine, identify, and graph inverse functions
•Explain the purpose of the horizontal line test
Lesson 10.1. Absolute Value, Piecewise, and Step Functions
REVIEW
Before beginning this chapter, you should be familiar with:
•solving and graphing linear equations and functions
•solving and graphing quadratic equations and functions
•solving and graphing exponential equations
•the standard and vertex forms of quadratic equations and functions
•function transformations, including translations, reflections, stretches, and compressions
•finding the domain and range of functions
•interval notation
Up until this point, the functions we’ve worked with have closely resembled the equations and expressions we worked with in the first section of this book. In this chapter, we’ll cover some special types of functions that you will probably be introduced to toward the end of your Algebra I course. Then we’ll learn about inverse functions and the horizontal line test. Finally, we will wrap up the chapter by discussing functions in the real world. (After all, you never know when you’ll need to compare functions to determine the perfect acceleration rate for catapulting pumpkins at the annual Pumpkin-Chucking Contest.)
First we’ll talk a little bit about absolute value. You should recall that the absolute value of a number is its distance from zero. Thus, the absolute value of any number is positive. For example, |4| = 4, |−4| = 4, and |−222| = 222.
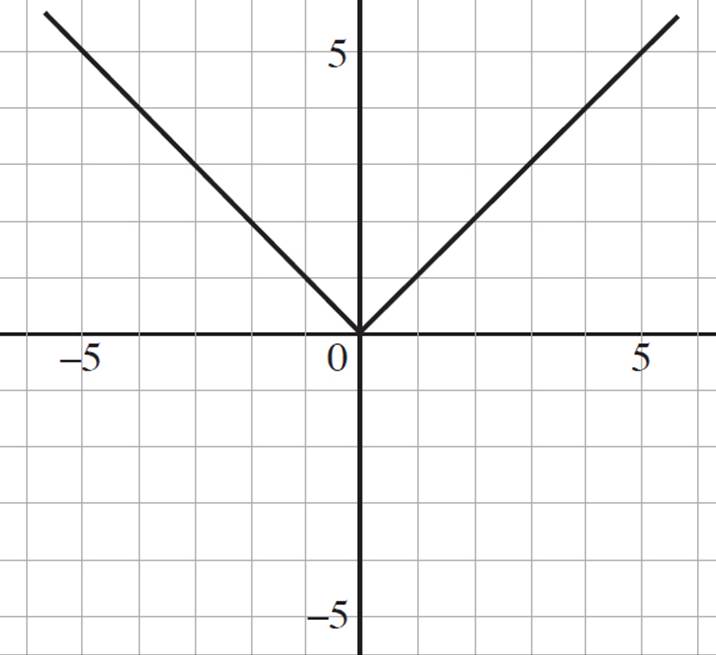
Because the absolute value of any number is positive, the graph of f(x) = |x|, shown in the following figure, has a domain of all real numbers but a range of all real numbers greater than or equal to zero.
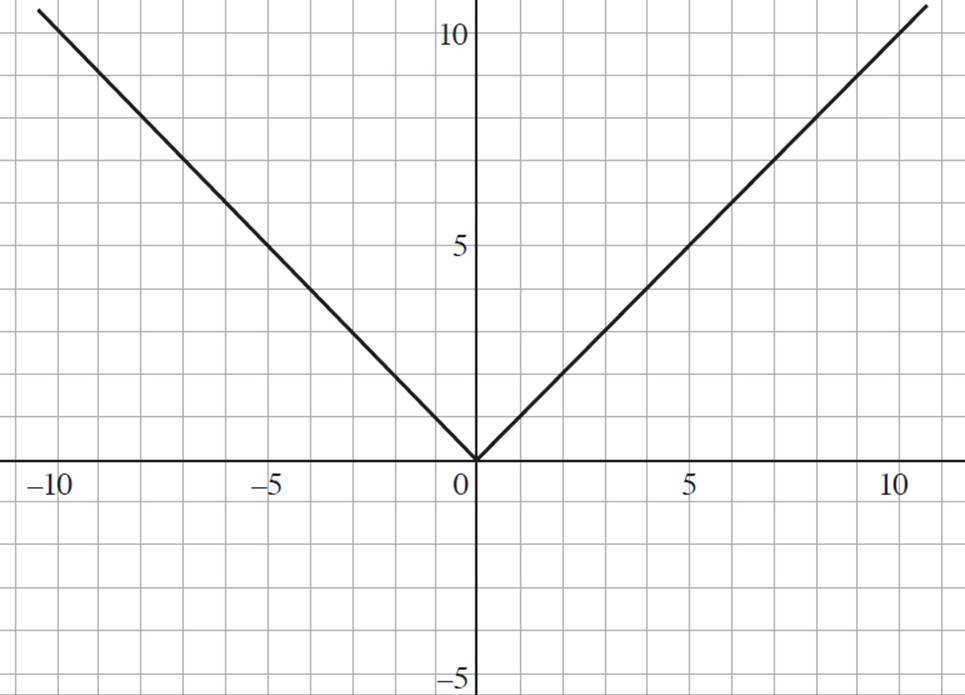
One of the key features of the absolute value graph is the “V” shape, which occurs because the absolute value is the distance from zero and, therefore, does not fall below the zero value on the y-axis. Whenever you encounter a graph that adheres to the V-shape, you are dealing with absolute value. You should also note that the absolute value graph is symmetrical. Even when manipulated through shifting or compressing, the symmetry of the absolute value graph will remain intact.
In all other aspects, however, you will treat the absolute value function as you would any other function. With that in mind, let’s try a couple of questions!
EXAMPLE 
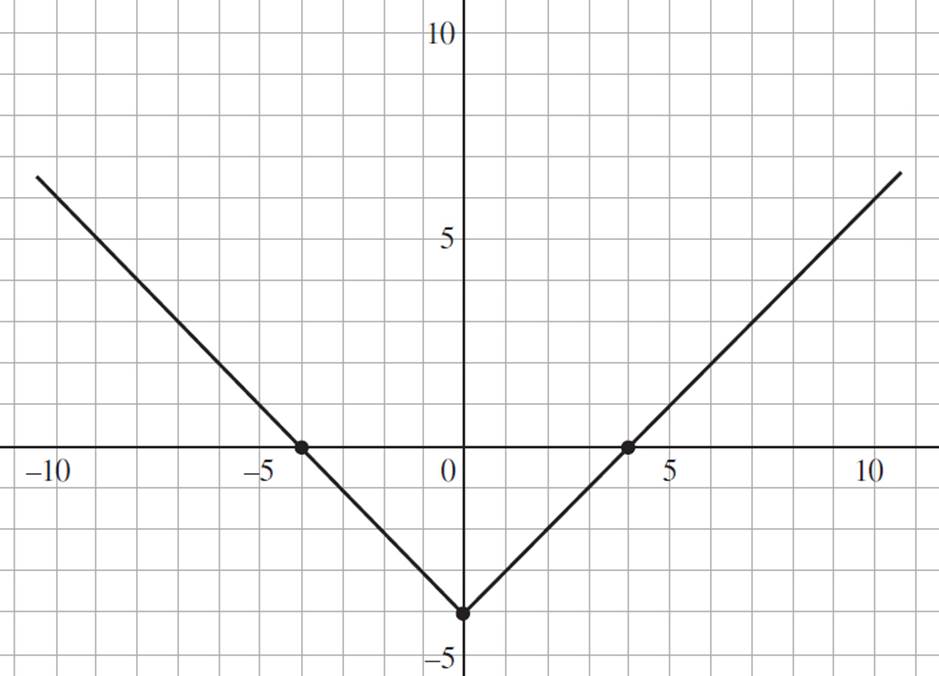
Given the graph of the function p(x) = |x| − 4, graph the function q(x) = −![]() p(x) + 2.
p(x) + 2.
Here you are given a graph that shows the function for absolute value, p(x) = |x| − 4 and asked to graph q(x). Therefore, you need to understand how q(x) is transformed from the original function, p(x).
First, consider −1/5 in the function q(x). Recall that for any function af(x) = y, if 0 < a < 1, the image will have a vertical compression in the y-direction appearing shorter and wider than the pre-image. Since q(x) = −1/5p(x) + 2, the value of a is 1/5, and the graph of the function will be vertically compressed by a factor of 5. We also know that for any function af(x) = y, the image will be reflected about the x-axis when a is negative.
Finally, you need to consider the value of 2 in the function q(x) = −1/5p(x) + 2. We know that if k > 0, for any function f(x) = x2 + k, the image will be shifted upwards by k units. Therefore, the graph of q(x) will be shifted up 2 units along the y-axis. Finally, we can put all of this information together to graph the function q(x) = −1/5p(x) + 2:

Great work! Now that you’ve manipulated a simple absolute value function, let’s try a question that’s a bit more involved.
EXAMPLE 
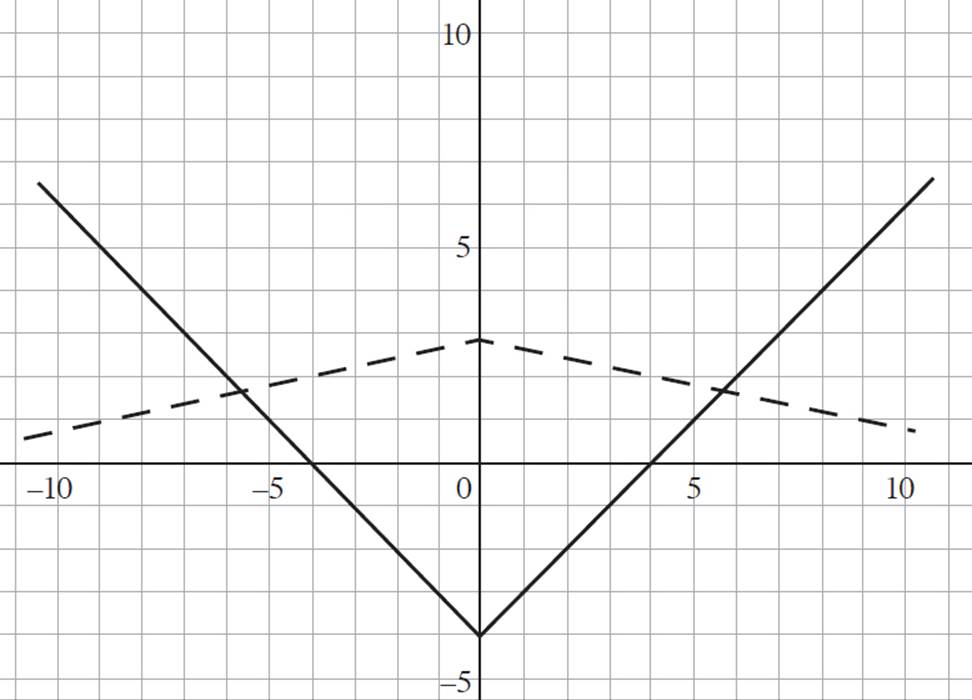
g(x) = 2f(x) + 2
h(x) = −f(x) − 2
j(x) = 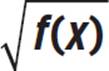
Given the graph of the function f(x) = |x|, and the functions g(x), h(x), and j(x), do the following:
a. Graph j(x) in the coordinate plane.
b. Graph g(x) and h(x) in the coordinate plane.
c. Determine h(5) + g(2).
d. Determine g(h(0)).
In order to answer this question, you need to understand how g(x), h(x), and j(x) are transformed from the original function, f(x). Tackle each transformed function one at a time.
First, you are asked to graph j(x), given that j(x) = 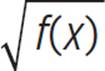 and f(x) = |x|. Since f(x) is the graph of absolute value of all real numbers, the graph of j(x) will be equivalent to the graph of the square root of all real numbers—not just the positive numbers: j(x) =
and f(x) = |x|. Since f(x) is the graph of absolute value of all real numbers, the graph of j(x) will be equivalent to the graph of the square root of all real numbers—not just the positive numbers: j(x) = 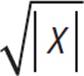 . If you forget how to graph the square root function, you can always plug in values for x to determine the corresponding y-value. Regardless of the method you use, the graph of j(x) is shown as a dark, dashed line in the graph on the following page.
. If you forget how to graph the square root function, you can always plug in values for x to determine the corresponding y-value. Regardless of the method you use, the graph of j(x) is shown as a dark, dashed line in the graph on the following page.
Now consider the function g(x) = 2f(x) + 2. In any function af(x) = y, the image will have a vertical stretch in the y-direction, appearing taller and thinner than the original image, when the value of a > 1. Here, the value of a = 2, indicating that the function g(x) has a vertical stretch by a factor of 2. We also know that if k > 0, for any function f(x) = x2 + k, the function shifts upwards by k units. Thus, the function g(x) = 2f(x) + 2 has a vertical shift upwards by two units. Based on this information, you can graph the function of g(x), as shown by the light dashed line in the graph on the next page.
Next, look at the function h(x) = −f(x) − 2. We know that for any function af(x) = y, the image will be reflected across the x-axis when the value of a < 1. Since the value of a is negative, the original image will be reflected about the x-axis. Furthermore, we know that if k < 0, for any function f(x) = x2 + k, the function shifts downwards by k units. Therefore, the function h(x) = −f(x) − 2 has a vertical shift downwards by two units. Use this information to graph the function of h(x), as shown by the light solid line in the following graph.
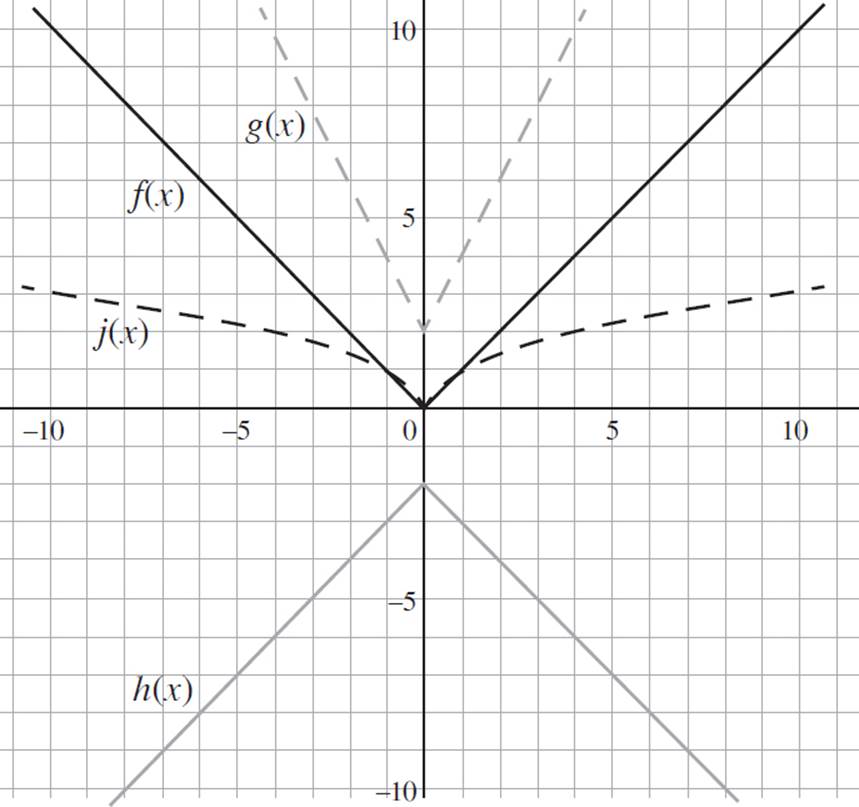
With the functions graphed, you now need to answer the third part of the question, which asks you to find the value of h(5) + g(2). Starting with the value h(5), find the y-value on the graph of h(x) when x = 5. Based on our graph, the value of h(5) = −7. Next, find the value of g(2) using the same process as before. Based on the graph, the value of g(2) = 6. Therefore, the value of h(5) + g(2) = −7 + 6 = −1.
Finally, you are asked to find the value of g(h(0)), which is function composition notation, used to represent composite functions. Function composition is the application of one function to the result of another function. So, for any function f(g(x)), sometimes written as (f o g)(x), the result of g(x) becomes the input for the function f(x). In this scenario, you are asked to find the value of g(h(0)). First, find the value of h(0). Based on our graph, h(0) = −2. The value of −2 will become the argument for g(x); that is, we are now looking for g(−2). Looking at the graph, g(−2) = 6. Therefore, the value of g(h(0)) = 6.

To review what we just did in the previous example, here’s the process for solving composite functions:
Solving Composite Functions
Step 1. If a composition function is written in the form (f o g)(x), rewrite it as f(g(x)).
Step 2. Replace each occurrence of x in the outside function, f(x), with the inside function, g(x).
Step 3. Simplify the answer.
Another special type of function is the piecewise function. Piecewise functions are comprised of at least two equations, or pieces, that are applied to different parts of the domain. Piecewise functions do not all have to be of the same form; for example, it is possible that the pieces can all be quadratic functions, or it is possible that the pieces are a combination of constant, linear, quadratic, cubic, exponential, or absolute value functions. In fact, there is no limit on the type of pieces in a piecewise function. Furthermore, piecewise functions can be continuous, having no breaks or holes in the function, or discontinuous, having breaks or holes in the function.
So, what does a piecewise function look like? Say that we’re given the following information:
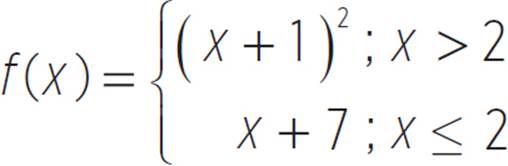
Domain: All Real Numbers
Range: All Real Numbers

Here is how you may see function composition on the ACT.
If f(a) = a2 + 3 and g(a) = 3a − 1, which of the following is an expression for g(f(a)) ?
F. a2 + 3a + 2
G. 3a2 − 3
H. −a2 + 3a − 2
J. 3a2 + 9a − 3
K. 3a2 + 8
Notice the format of a piecewise function: Instead of f(x) being set equal to a single function, it is set equal to all the pieces of the function. Now you just need to graph the pieces according to the rules stated in the function. Here you are told that when x > 2, the function (x + 1)2 is graphed, and when x ≤ 2, the function x + 7 is graphed. Apart from these conditions, you will graph the function as you usually would. The graph of our piecewise function will look like this:
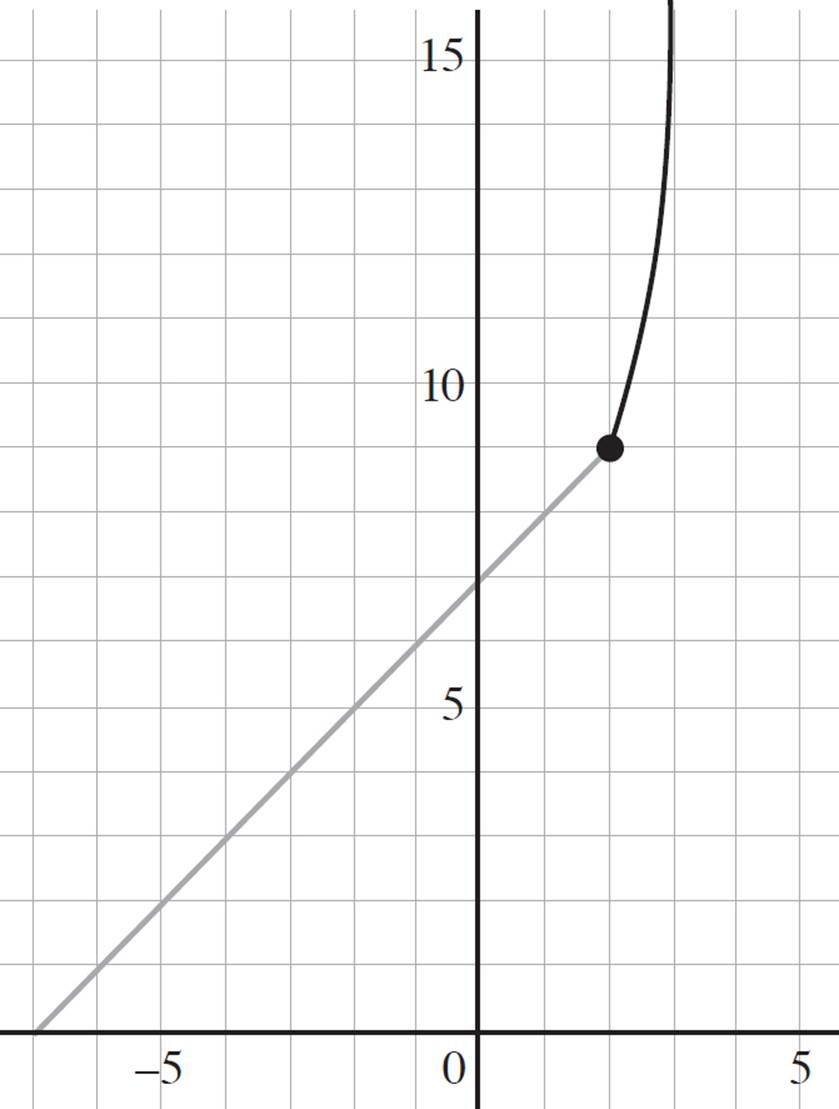
Notice that there is a closed dot joining the two pieces of the function. A closed, or solid, dot indicates that the value is included in the piece of the function, while an open, or unfilled, dot indicates that the value is not included in the piece of the function.
In this situation, the piecewise function is continuous because there are no holes or gaps. The second piece of the function, f(x) = x + 7, is true when x ≤ 2. Thus, since the function exists at x = 2, there is no gap in the function and the function is continuous.
Now that we’ve covered the basics of piecewise functions, let’s see a couple of examples.
EXAMPLE 
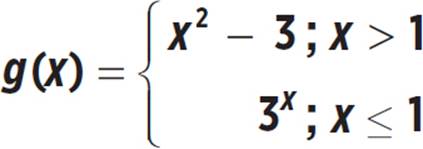
Doman: All Real Numbers
Range: y > −2
Given the information above, graph the function and determine whether it is continuous or discontinuous. If the function is discontinuous, state where the gaps, holes, or breaks occur.
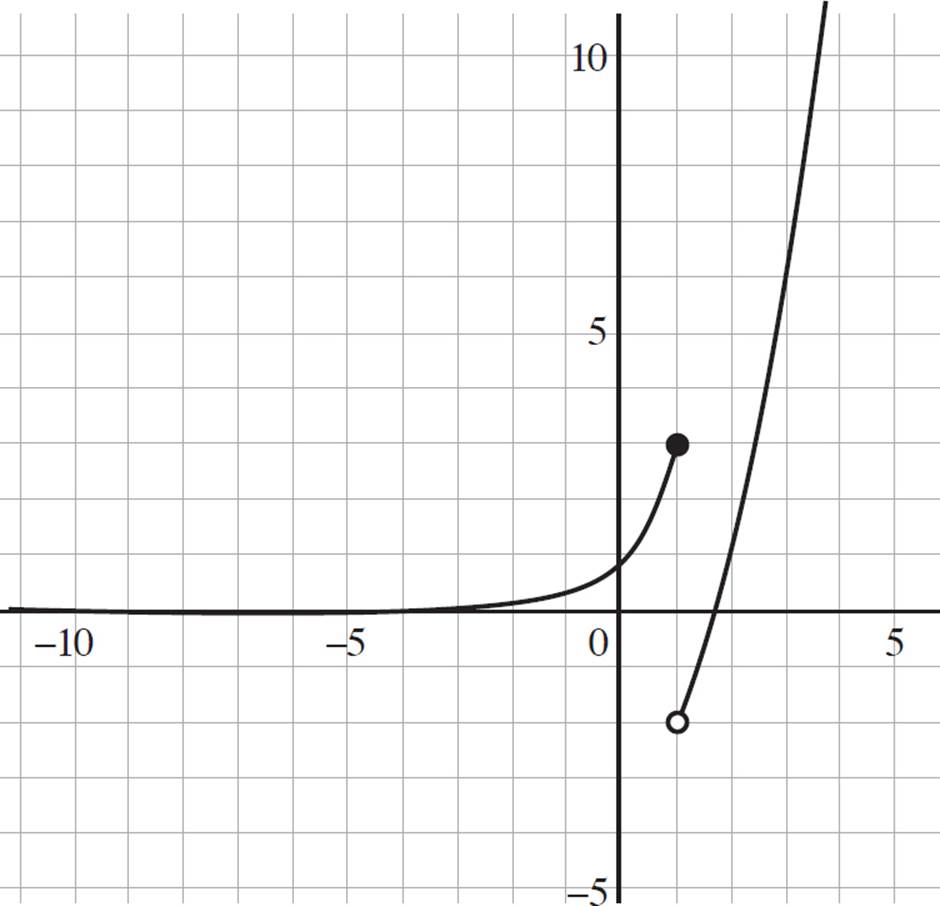
Here you are given a piecewise function where g(x) = x2 − 3 when x > 1, g(x) = 3x when x ≤ 1, and both the domain and range of g(x) is y > −2. First, you need to graph the two pieces of the function.
Using the skills you gained in Chapter 9, you know that g(x) = x2 − 3 is simply the graph of x2 shifted down three units on the y-axis. However, you will only graph the piece of the function when x > 1 in the coordinate plane. Similarly, you will use your knowledge of graphing exponential equations to graph the second piece, g(x) = 3x. For this piece, however, you will only graph the function when x ≤ 1 in the coordinate plane. Your final graph should look like the following:

Here you’re asked to find the value of g(f(a)), which requires you to use the function composition skills discussed previously. For the function g(f(a)), the result of f(a) becomes the input for the function g(a). Since f(a) = a2 + 3, we need to find g(a2 + 3). When we work through the question, we find that
g(a2 + 3) = 3(a2 + 3) − 1
g(a2 + 3) = 3a2 + 9 − 1
g(a2 + 3) = 3a2 + 8
Therefore, the expression g(f(a)) is equivalent to 3a2 + 8, or (K).
Now determine whether the function is continuous or discontinuous. Unlike the previous example, this function has a clear break in continuity at x = 1; the exponential function has a y-value of 3 when x = 1, while the quadratic function has a y-value of −2 when x = 1. Thus, this break in the function means that the function is discontinuous at x = 1.

EXAMPLE 
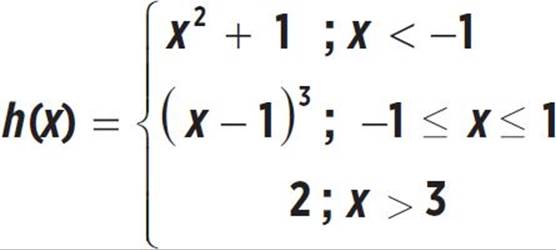
Doman: (−∞, ∞)
Range: [−8, ∞)
Given the information above:
a. Graph h(x) in the coordinate plane.
b. Identify h(−3) and h(2).
c. State whether the function is continuous or discontinuous.
There’s a lot happening in this question, but you’ll be fine if you tackle it piece by piece. You are told that h(x) = x2 + 1 when x < −1, h(x) = (x − 1)3 when −1 ≤ x ≤ 1, and h(x) = 2 when x > 3. You are also told that the domain is all real numbers and the range is [−8, ∞). Start by graphing each piece of the function in turn, according to the conditions of the function.
Again, you can use the information you learned about quadratic functions to graph the first piece, h(x) = x2 + 1 when x < −1, knowing that this is the basic quadratic function shifted up one unit on the y-axis. Next, you need to graph the second piece, h(x) = (x− 1)3 when −1 ≤ x ≤ 1. Since we haven’t spent a great deal of time on cubic functions, you may find it easiest to plug in the values of x for which the function exists and find the associated f(x) output values. By plugging into h(x) = (x − 1)3, you will find the following plot points: (−2, −27), (−1, −8), (0, −1), and (1, 0). Finally, you need to graph the third piece of the function, h(x) = 2 when x > 3. When you put it all together, you will have the graph on the following page.
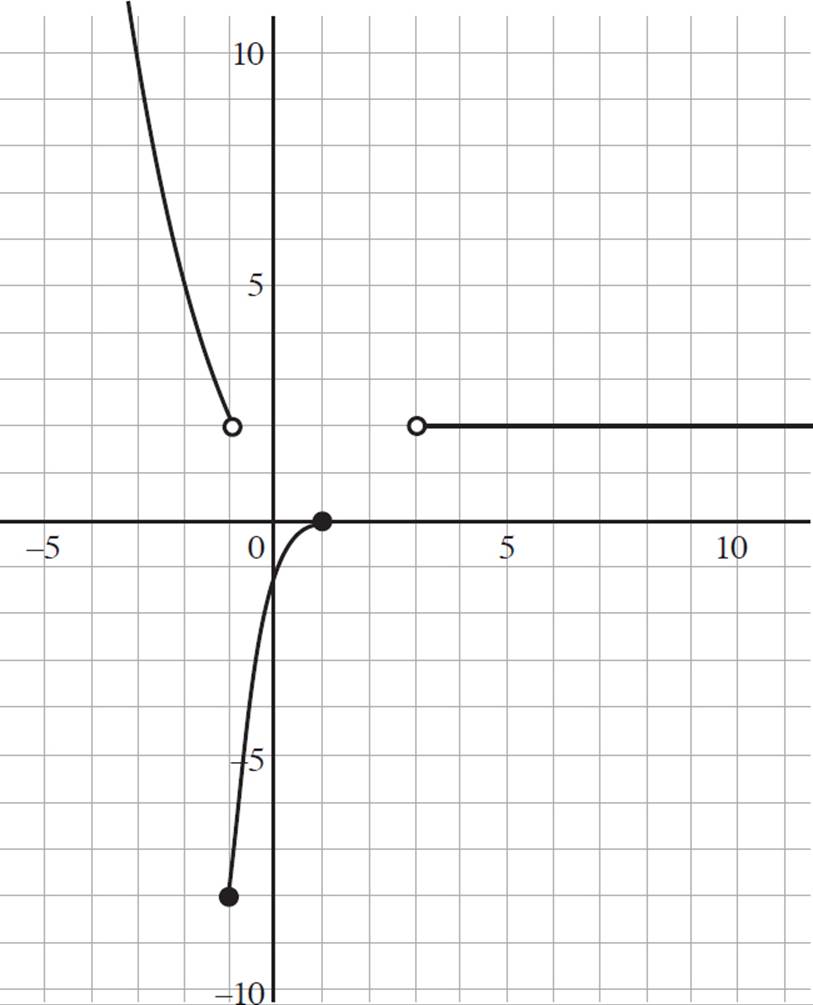
Next, you are asked to determine h(−3) and h(2). Just like you did in previous questions, you will find the value of h(−3) by finding the y-value when x = −3 on the graph. Based on the graph, h(−3) = 10. Now, repeat the process to find h(2). Don’t worry if the point you’re working with doesn’t exist on the function; if that is the case, simply say that. In this scenario, h(2) does not exist.
Finally, the question requires you to determine if the function is continuous or discontinuous. Looking at the graph, the answer should be fairly evident to you: Due to the multiple breaks and gaps in the function, the function is discontinuous.

The last special type of function that we are going to discuss is the step function, which is related to the piecewise function. A step function is a piecewise function that consists of constant horizontal pieces occurring at adjacent intervals of the function; the function ends up looking like a set of steps, or a staircase. All step functions are discontinuous, as it is impossible to construct a step function that consists of joined pieces.
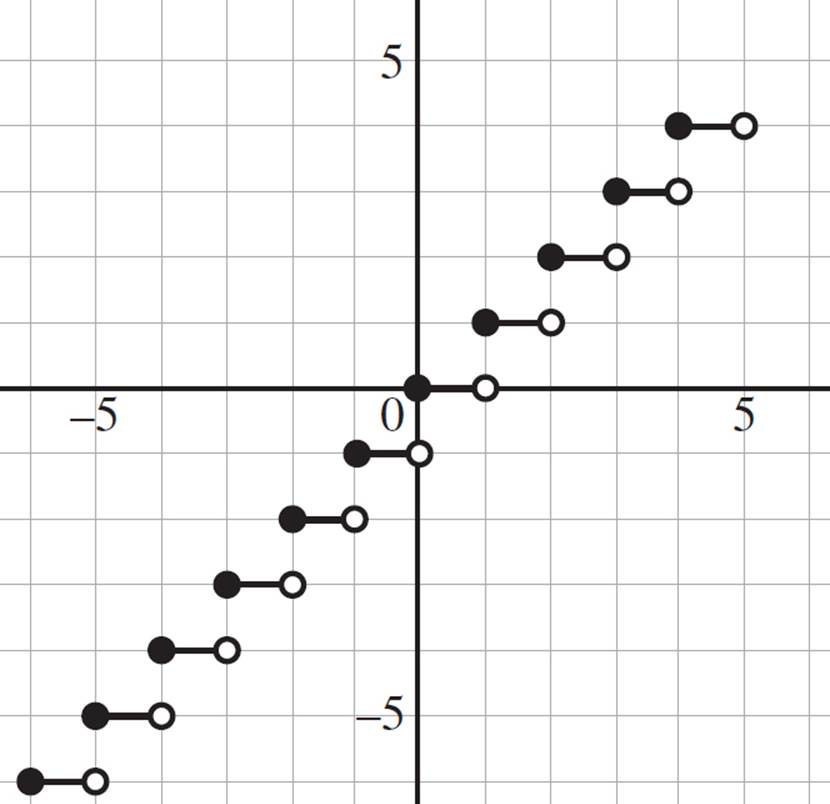
One well-known step function that mathematicians love is the greatest integer function, denoted by f(x) = [x]. The greatest integer function returns the largest integer less than or equal to x for all inputs x; in short, the function rounds each real number down to the nearest integer. So, for example, f(−5.5) = [−5.5] = −6, f(−3) = [−3] = −3, and f(1.5) = [1.5] = 1. The graph of f(x) = [x] is as follows:
The greatest integer function is just one example of a step function. Sometimes it is necessary to provide more information regarding the way in which the numbers are rounded. This is where floor and ceiling functions come into play.
A floor function, denoted as floor[x], returns the greatest integer that is less than or equal to x.
A ceiling function, denoted as ceil[x], returns the least integer that is greater than or equal to x.
However, if you need to determine the floor or ceiling of an integer, there is no change. The following table shows how the value of x is affected by floor and ceiling functions.
|
x |
Floor |
Ceiling |
|
−2.4 |
−3 |
−2 |
|
−0.5 |
−1 |
0 |
|
0 |
0 |
0 |
|
3.8 |
3 |
4 |
|
5 |
5 |
5 |
Let’s try a question involving step functions.
EXAMPLE 
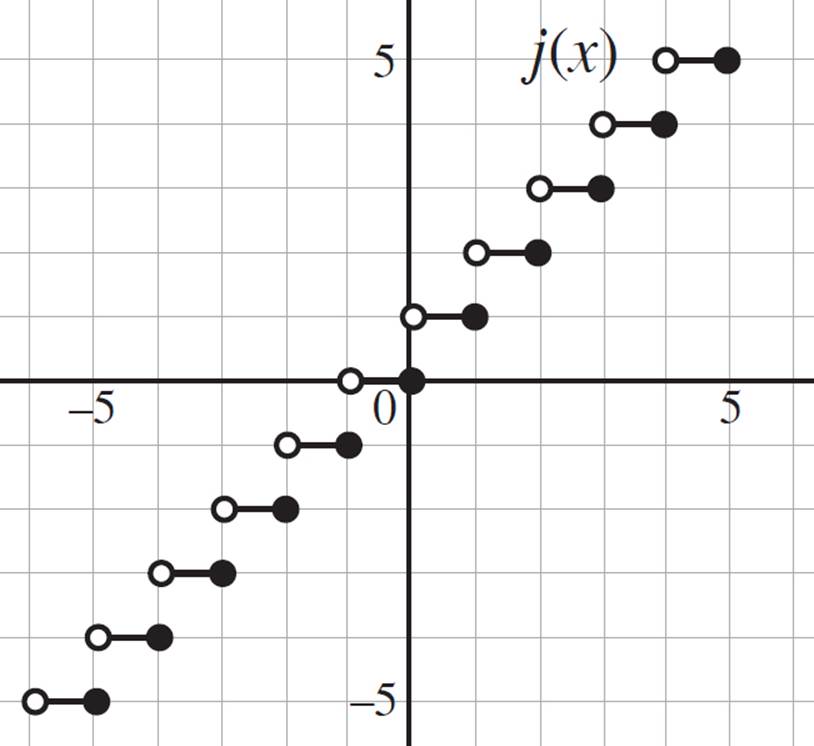
Based on the graph of j(x):
a. State whether the function is a floor function or a ceiling function.
b. State whether the function is continuous or discontinuous.
c. Determine the value of j(−2.4) and j(4).
This question requires you to analyze the given step function. Does it look similar to the greatest integer function? Hopefully, you answered “yes.” But what’s different here?
Unlike the greatest integer function, which is a floor function, the function j(x) returns the least integer that is greater than or equal to x. For example, j(−3.4) = −3 and j(2.6) = 3. The function j(x), therefore, is a ceiling function. Furthermore, the function j(x) is a discontinuous function, a characteristic of all step functions, as indicated by the gaps between the pieces of the function.
Finally, you need to determine the value of j(−2.4) and j(4). Since j(x) is a ceiling function, the value of j(−2.4) = −2. However, in any step function, the value of an integer is the integer itself. Therefore, the value of j(4) = 4.

Well done! You conquered your first step function question. Now let’s try a more complex example.
EXAMPLE 
Given the function q(x) = (floor[x])2, graph q(x) in the coordinate plane and state whether the function is continuous or discontinuous. Then identify q(0) and q(−1.2).
Here you are told that q(x) = (floor[x])2. But we haven’t worked with a quadratic step function! No worries. If you aren’t sure how the quadratic step function is graphed, plug in for x to find the associated value of f(x). When you do so, you will find the following values:
|
x |
q(x) |
|
−4 |
16 |
|
−3 |
9 |
|
−2 |
4 |
|
−1 |
1 |
|
0 |
0 |
|
1 |
1 |
|
2 |
4 |
|
3 |
9 |
|
4 |
16 |
Now you can graph the quadratic step function, taking into account that q(x) is a floor function.
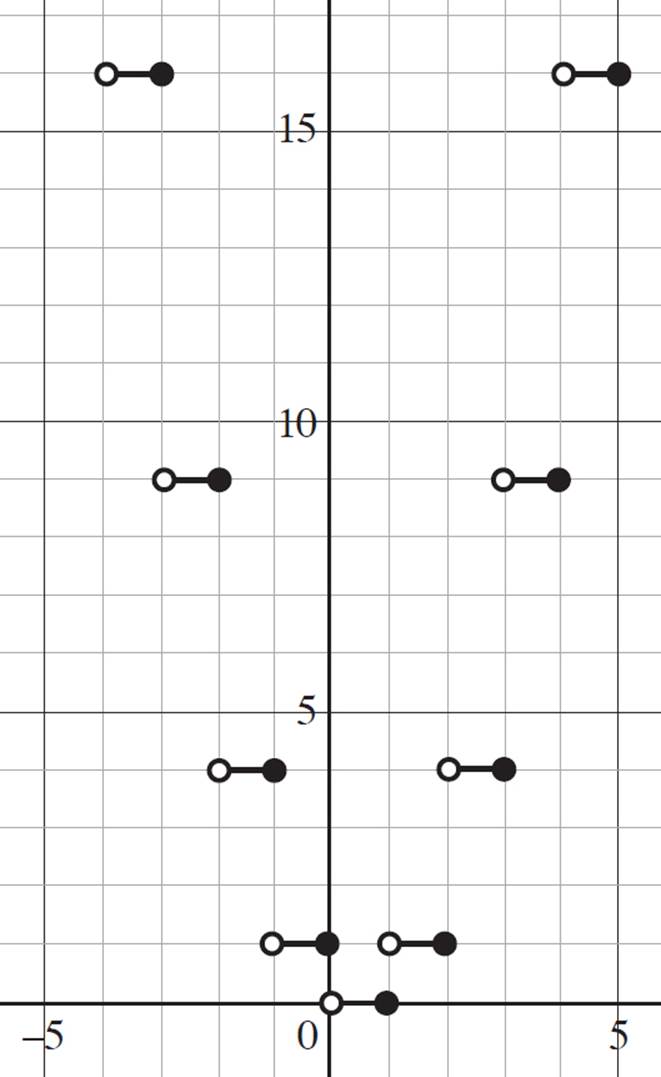
Next, determine the values of q(0) and q(−1.2). Recall that in any step function the value of an integer is the integer itself. Therefore, the value of q(0) = 0. Now find the value of q(−1.2). Since a floor function returns the greatest integer that is less than or equal to x, the value of q(−1.2) = 4.
You’re done! You’ve successfully conquered a quadratic step function.
