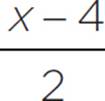High School Algebra I Unlocked (2016)
Chapter 10. Other Functions
Lesson 10.2. Inverse Functions
You may agree that one of the most amazing features of a cell phone is the caller ID feature. After all, most people like to know who is contacting them before they answer the phone. And believe it or not, caller ID technology is an inverse function. How, you ask? Well, let’s think about this.
Imagine that you want to find someone’s number in your cell phone. In this scenario, you search for that person’s name and you find his or her number; the input is the person’s name, and the output is the person’s telephone number. On the other hand, when someone calls you, the input is the phone number, and the output is the person’s name that shows up on your caller ID.
Therefore, the function is number → name, and the inverse function is name → number.
Just like in the previous real-world example, an inverse function is a function that undoes the action of a function and replaces the dependent and independent variables of the original function. So, if a function takes an input value, performs an operation, and produces an output value, the inverse function will take the output value, perform an operation, and produce the original input value.
In the world of mathematics, there is a specific notation used for inverse functions: a function f(x) has an inverse function denoted as f−1(x). So, in our previous Caller ID example, the original and inverse functions would look as follows:
Original Function f(x)
1(800)-555-5555 → Trumplestiltskin Incorporated
Inverse Function f−1(x)
Trumplestiltskin Incorporated → 1(800)-555-5555
In math, a function f has an inverse function g whenever y = f(x) and x = g(y). In other words, a function has an inverse function only if there is only one x-value for every y-value in the original function; essentially, the inverse function has all of the same points as the original function, but the x- and y-values are reversed. Let’s see how this works.
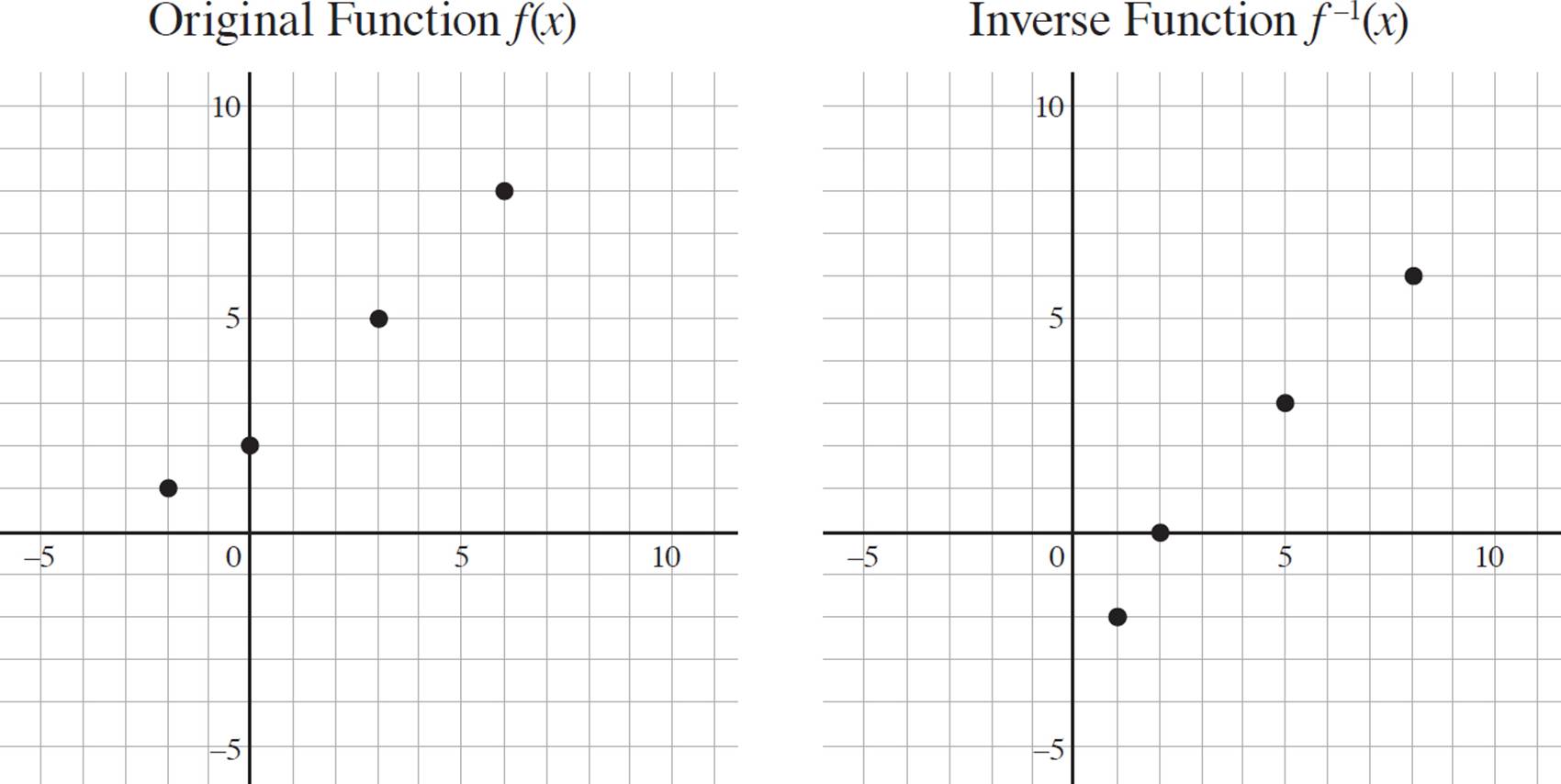
Imagine that function f(x) is composed of the following points: {(−2, 1), (0, 2), (3, 5), (6, 8)}. If you were to plot these points on the coordinate plane, the result would be the graph below (Original Function). Based on the plot points of f(x), you could then find the plot points for the inverse function, f−1(x), by switching the x- and y-values. Therefore, the function f−1(x) is composed of the points (1, −2), (2, 0), (5, 3), and (8, 6), and is graphed as shown (Inverse Function).

Here is how you may see real-world application of functions on the SAT.
Bacteria grow asexually by a single bacterium dividing into two bacteria. These bacteria can themselves divide again and again. Assume a petri dish contains a single bacterium that divides exactly once per hour. Which of the following functions, f(t), represents the number of bacteria in the petri dish after t hours?
A) f(t) = 2t
B) f(t) = 2t
C) f(t) = (t + 1)2
D) f(t) = t2
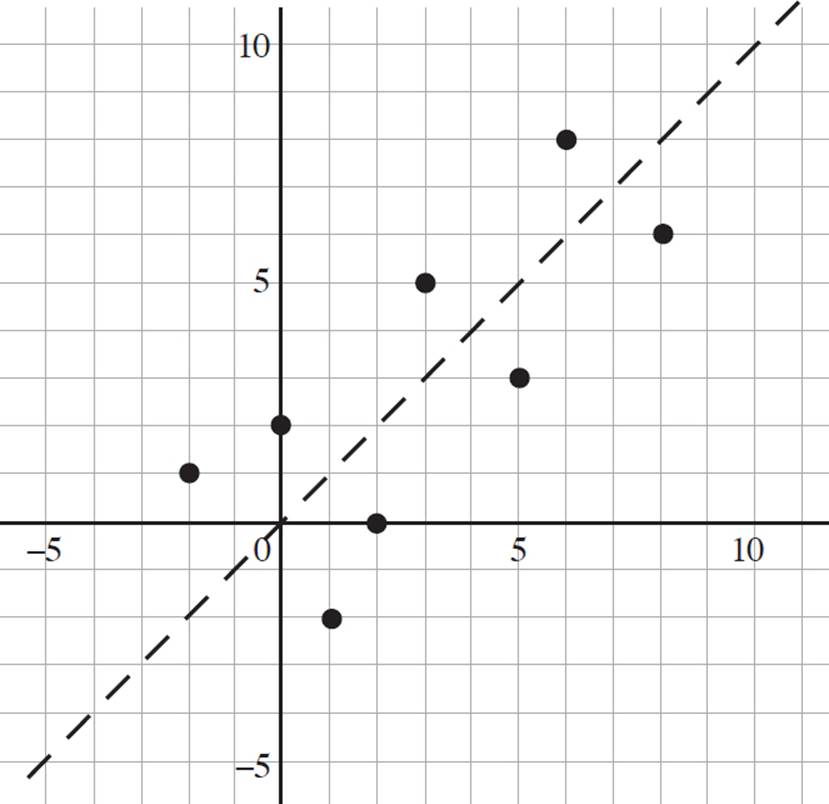
Individually, these graphs may not look that impressive, but let’s look at what happens when the two graphs are combined. Notice that the inverse function is simply the original function reflected across the line x = y. This shows that there is a distinct relationship between a function and its inverse. Refer to the following graph.
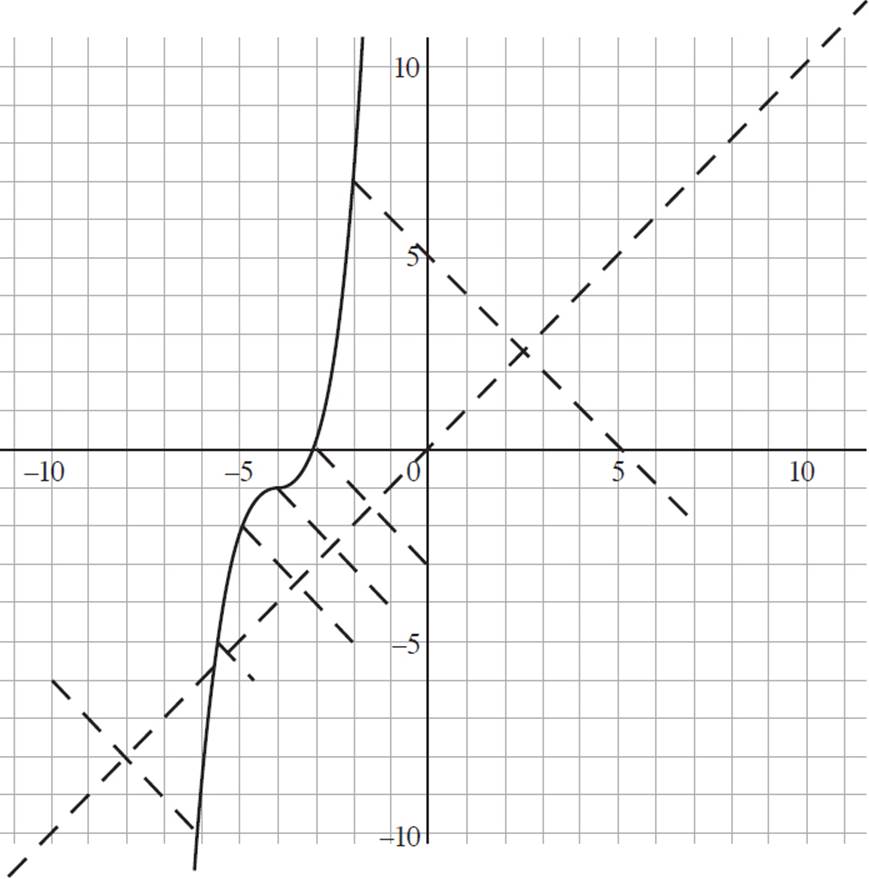
Using the power of reflection, you can determine the inverse of a function without knowing anything about the function itself. For example, imagine that you were asked to sketch the inverse of function g(x), shown in the following graph.
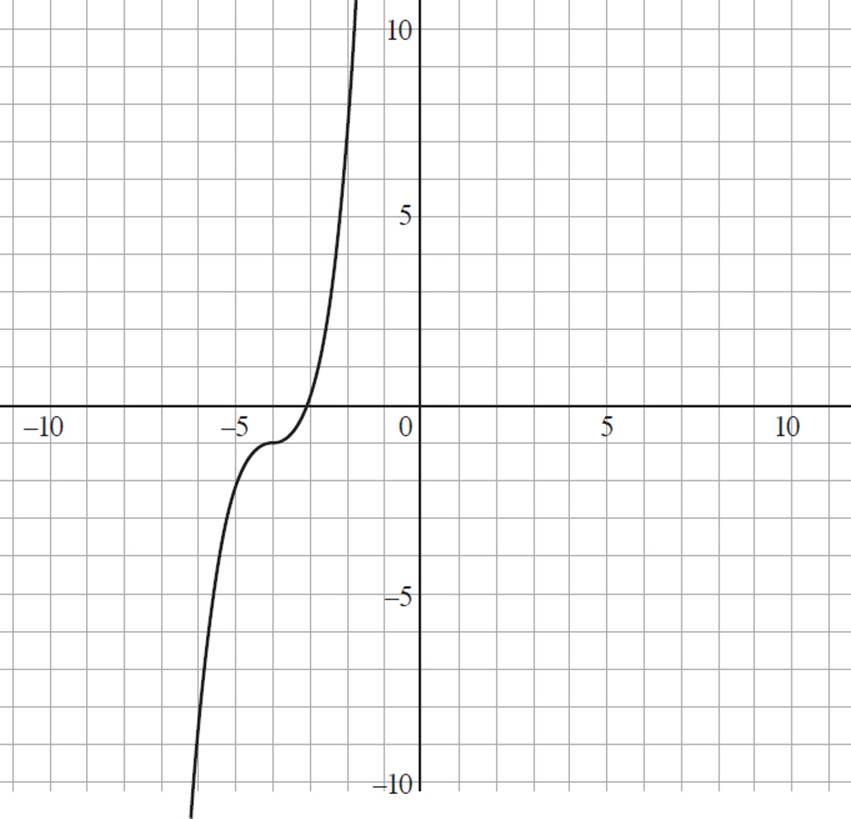
How would you find the inverse of g(x)? Start by drawing your reflection line. Once your reflection line is drawn, you can draw lines from points on g(x) to the reflections of those points, which will fall on g−1(x). Note that points that fall on the reflection line are the same in both the original and inverse function.

Pay attention to what’s going on in the question. You’re told that bacteria grow when a single bacteria divides into two bacteria every hour, and that this process keeps going and going. The question asks you to determine the function that represents the number of bacteria after t hours. So, figure out what’s happening here. If you started with a single bacterium, this would divide into two bacteria after one hour. After two hours, each of these bacteria would then split, resulting in four bacteria, and, after three hours, the bacteria would split again into eight bacteria, and so on. Does this type of doubling growth seem familiar to you? It should! This is an example of exponential growth, a real-life example of an exponential equation. Therefore, we know that we need a function that also models such exponential growth.
Since we know that the bacteria double every hour, and we want a function that tells us the number of bacteria after t hours, we are essentially multiplying 2 by itself t times. Thus, our function will be f(t) = 2t, or (B).
What if you didn’t remember how to construct an exponential growth? If you look at the answer choices, only one function is exponential. Choice (A), f(t) = 2t, is a linear function, and both (C) and (D), f(t) = (t + 1)2 and f(t) = t2, are both quadratic functions; thus, they can all be eliminated.
Once you’ve graphed the reflection lines, you can connect the ends of the reflection lines to graph the inverse function.
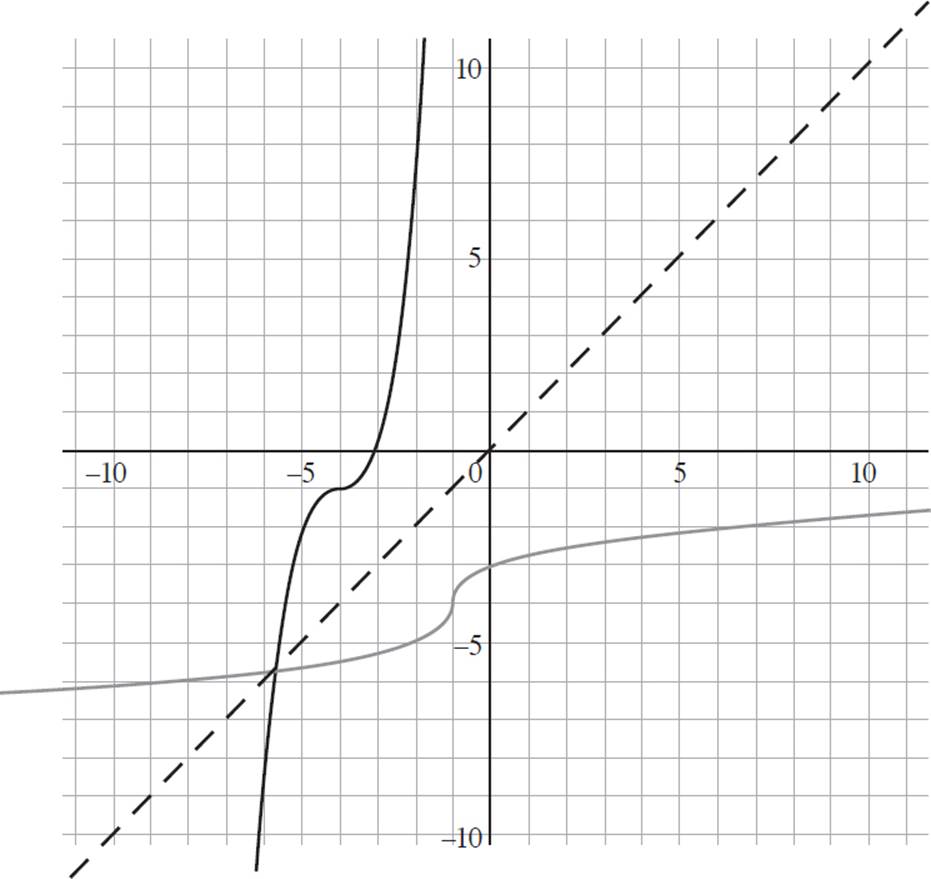
And without even knowing that g(x) = (x + 3)3 − 1, you were able to graph the inverse function, g−1(x) = ![]() − 4.
− 4.
You won’t always be asked to draw an inverse function without knowing the original function. In fact, teachers love asking students to determine the inverse function based on the original function. We said that an inverse function simply reverses the x- and y-values, but how do we come up with the equation of an inverse function? Luckily, there is a process for this.
Solving for the Inverse of a Function
|
Steps |
f(x) = 2x + 4 |
|
1. Given a function, replace the term f(x) with y. |
y = 2x + 4 |
|
2. Switch the x- and y-terms. |
x = 2y + 4 |
|
3. Solve for y. |
2y = x − 4 and y = |
|
4. Replace y with f−1(x). |
f−1(x) = |
You may encounter a tricky question in which you’re asked to find the inverse of a function—but the inverse is not actually a function!
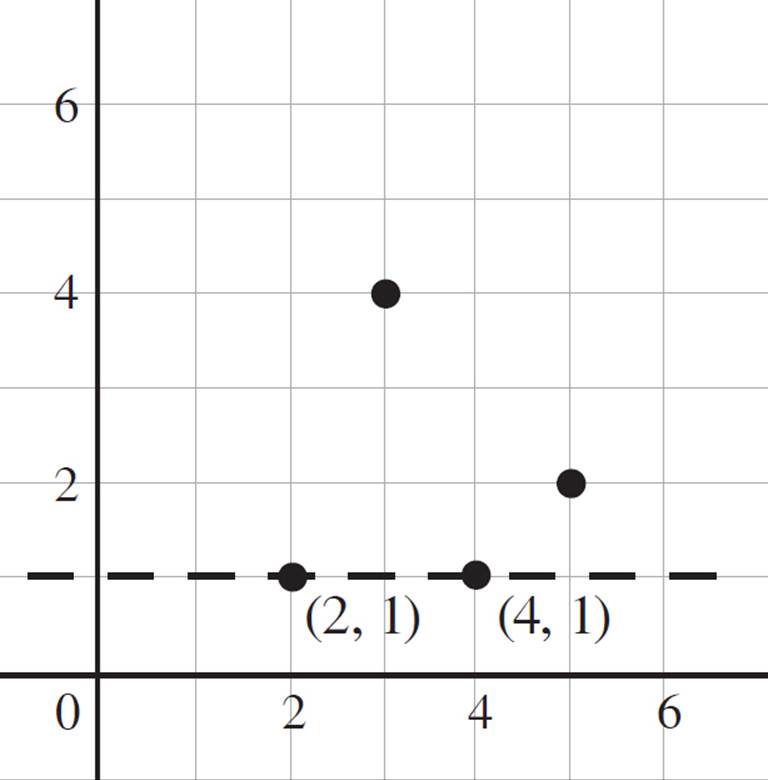
For example, say you’re told that h(x) consists of the points (2, 1), (3, 4), (4, 1), and (5, 2). Graphically, your function would look like the graph on the left below. So far, so good, right? Using the same technique as before, you would assume that h−1(x) consists of the points (1, 2), (4, 3), (1, 4), and (2, 5), as shown in the graph on the right:
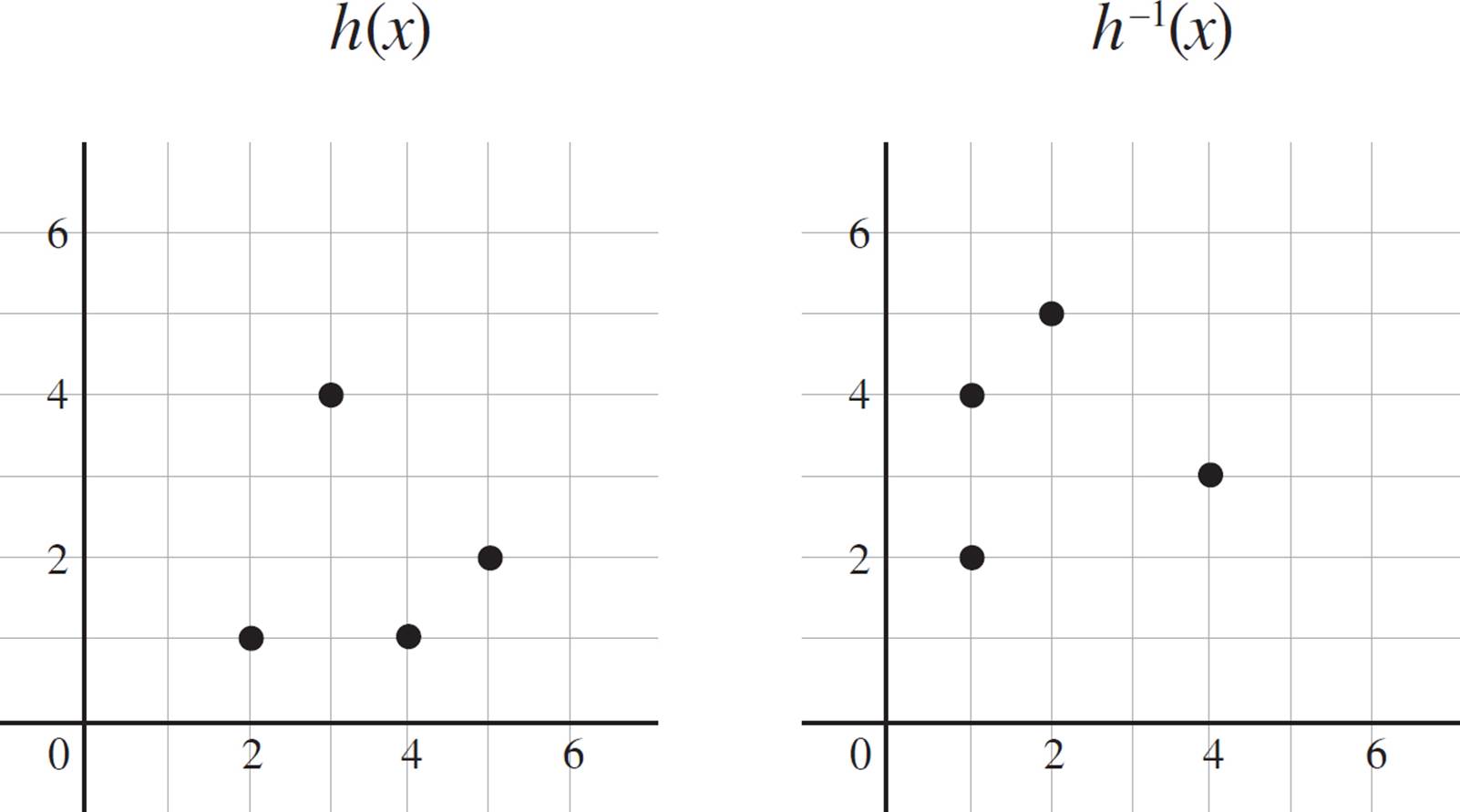
But when you plot the inverse, you will see that there is more than one y-value associated with x = 1. As you might recall, a function must have a single y-value associated with each x-value. Thus, the inverse of h(x) fails the vertical line test and is not a function.
Plotting the potential inverse of a function is time consuming. Thankfully, however, mathematicians observed that you can determine whether a function has an inverse by using the horizontal line test. If you guessed that the horizontal line test is related to the vertical line test, you are correct! The horizontal line test is used to determine whether every y-value in a function has only one unique x-value.
So, if we were to look at the function h(x) again, we would notice that it fails the horizontal line test, as there are two x-values when y = 1. Since h(x) did not pass the horizontal line test (as shown on the following graph), we can safely state that the function h(x) does not have an inverse function.
Okay, it’s time for a few questions.
EXAMPLE 
Given that function d(x) consists of the points {(−2, 3), (−0.5, 4), (0, 1), (2, 2), (3, 5)}:
a. Graph d(x) in the coordinate plane.
b. Determine if d(x) has an inverse function.
c. If d−1(x) exists, draw the line of reflection and graph d−1(x) in the coordinate plane.
As always, take this multi-part question one step at a time. Start by graphing d(x) in the coordinate plane. The result should be a graph similar to the following graph labeled d(x).
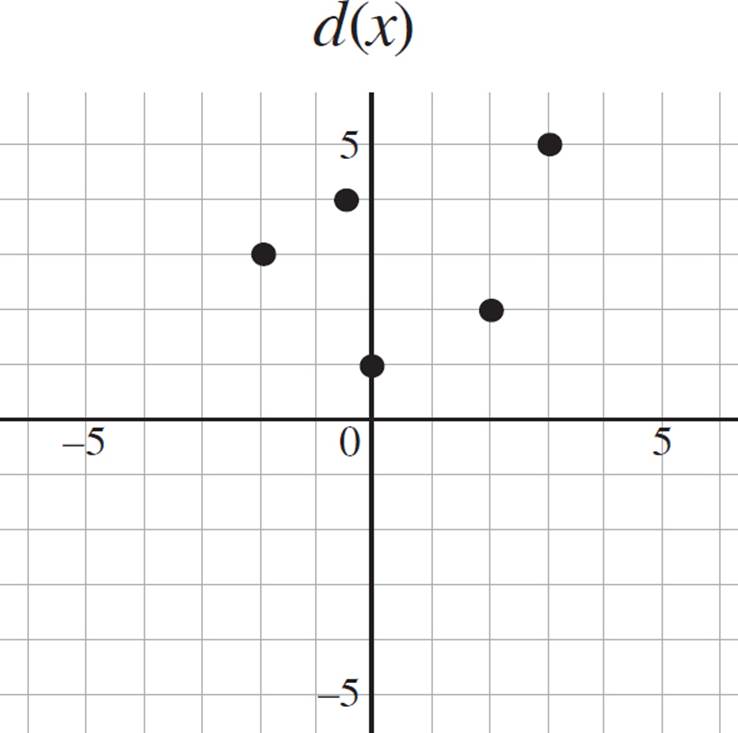
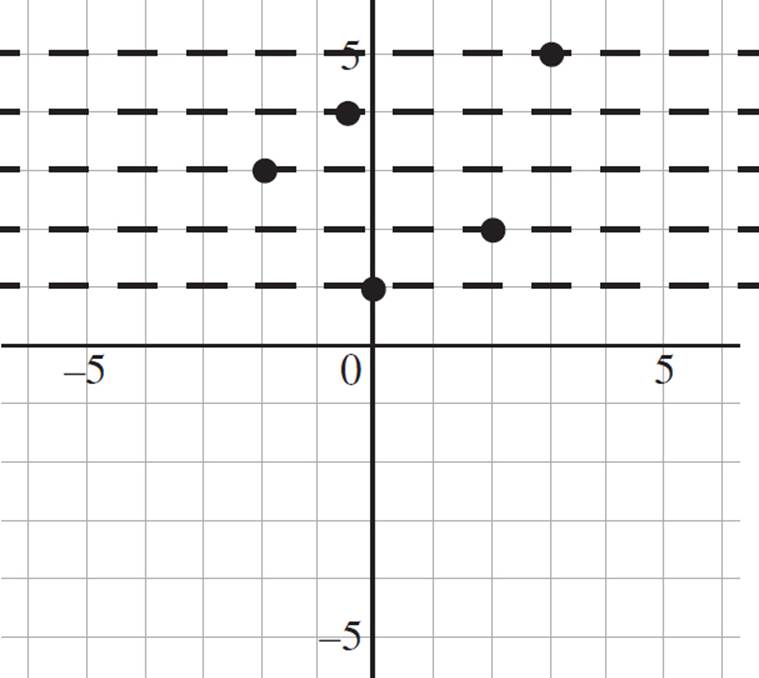
Next, the question asks you to perform the horizontal line test to determine if d(x) has an inverse. After conducting the horizontal line test, as shown on the following graph, you will notice that there is a single x-value associated with each y-value. Thus, d(x) passes the horizontal line test and, therefore, has an inverse.
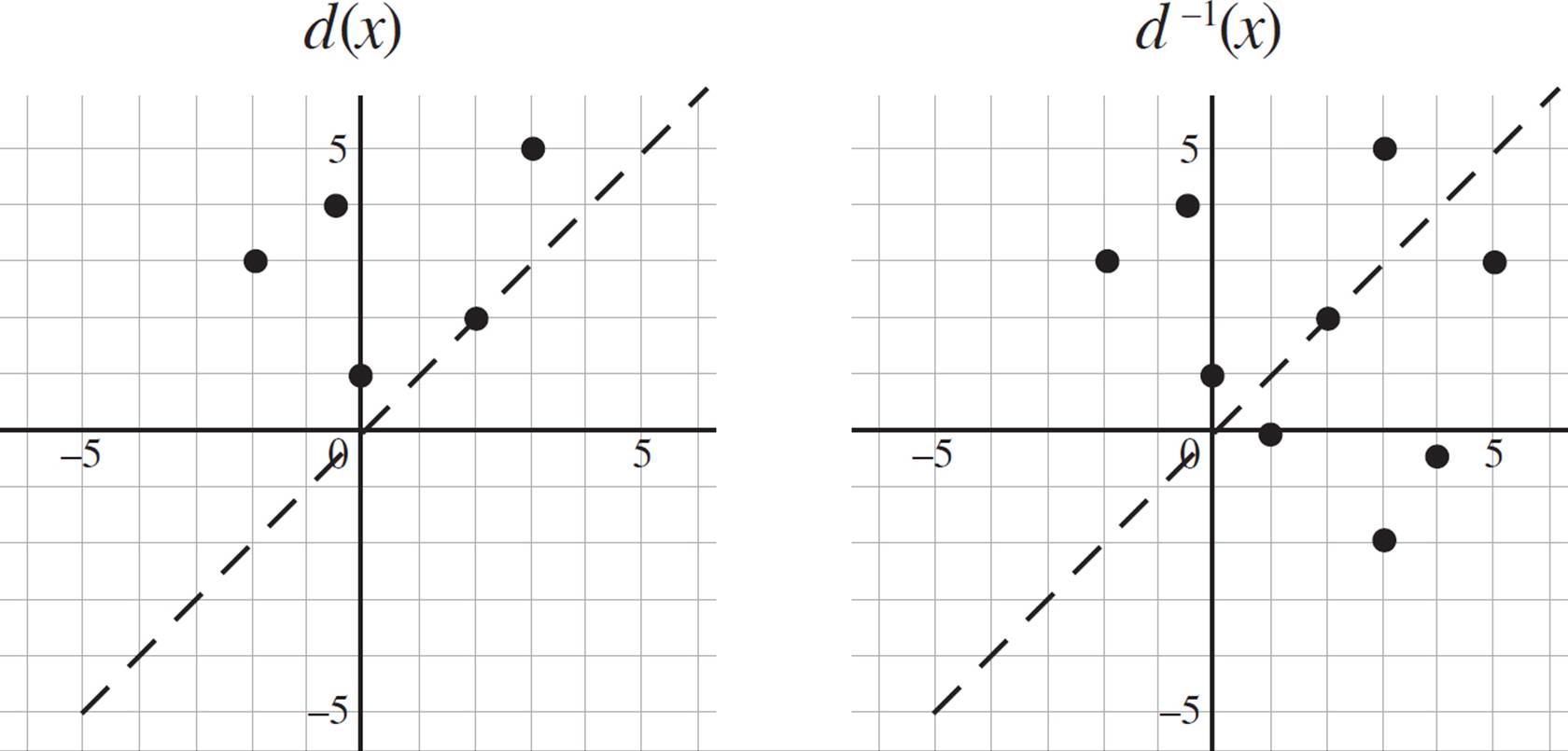
Additionally, the question asks you to draw the line of reflection in the coordinate plane. Once you’ve drawn the line of reflection, you can graph d−1(x) in the coordinate plane. If you aren’t comfortable only using the line of reflection to plot the points of the inverse function, you can always just switch the x- and y-values in d(x). If you choose to do this, you will find that d−1(x) consists of the points {(3, −2), (4, −0.5), (1, 0), (2, 2), (5, 3)}. Your d−1(x) graph will look like this:

EXAMPLE 
Given the function h(x) = x2 + 2:
a. Graph h(x) in the coordinate plane.
b. Determine if h(x) has an inverse function.
c. If h−1(x) exists, draw the line of reflection and graph h−1(x) in the coordinate plane.
As with the previous example, start by graphing h(x) in the coordinate plane. Refer to the graph on the left below. You should recognize that h(x) is the basic quadratic function shifted up two units on the y-axis.
Once you’ve graphed h(x), determine if h(x) has an inverse by performing the horizontal line test. As you can see from the graph on the right, h(x) fails the test miserably. But this makes sense: Because quadratics form symmetrical parabolas, each y-value will be associated with a pair of x-values. Therefore, h(x) does not have an inverse.
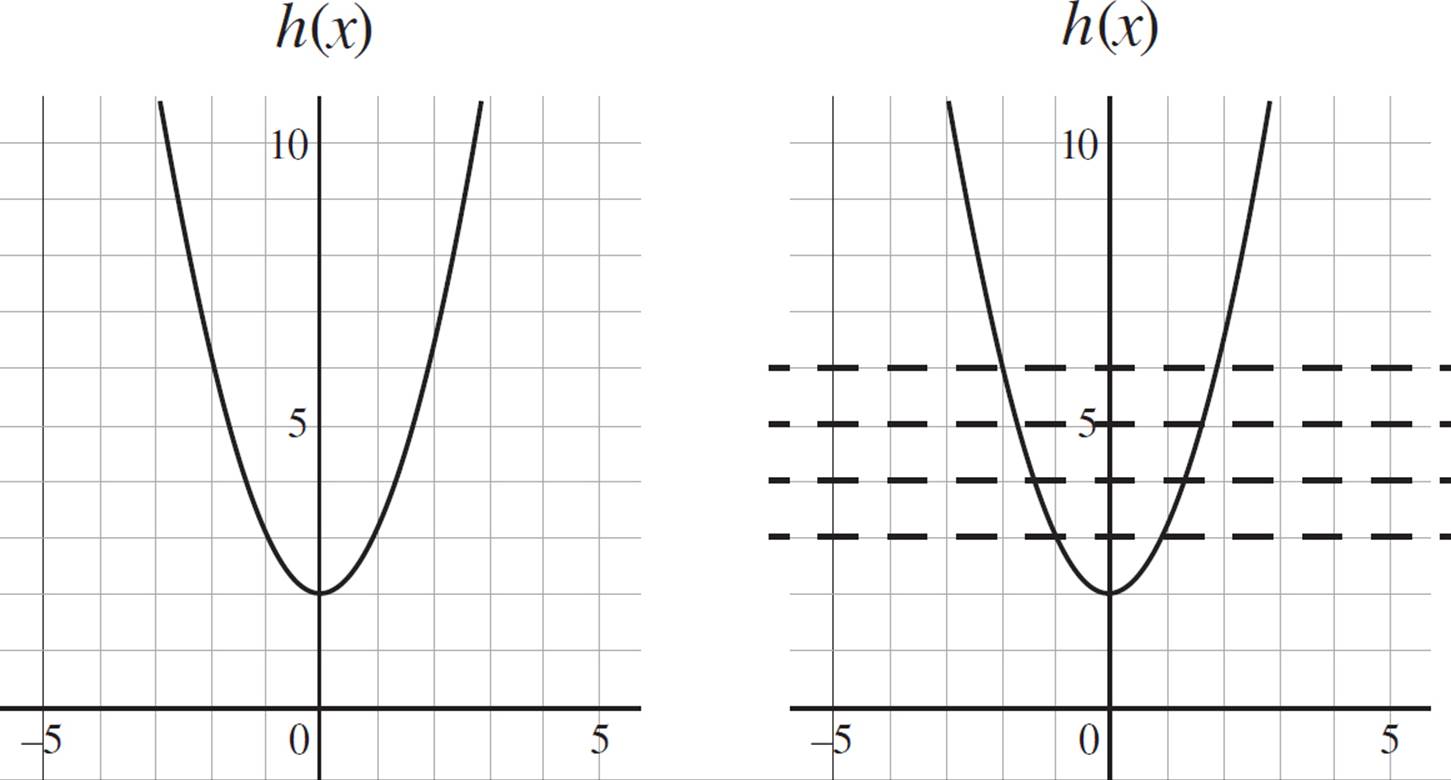

Note: If you notice that a function is going to pass the horizontal line test, as in the case of a linear function, you don’t need to draw horizontal lines through the entire graph. While you want to be accurate, you also want to be efficient!
EXAMPLE 
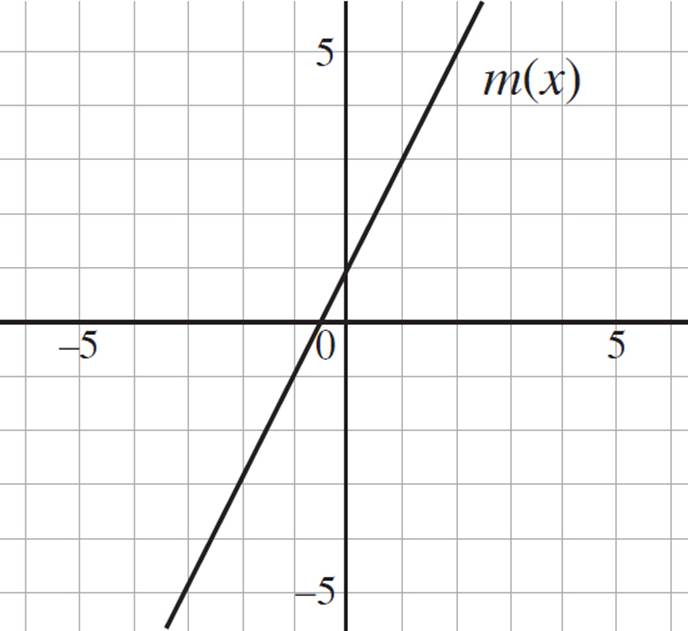
Given the graph of m(x), determine if m(x) has an inverse function. If so, draw m−1(x) in the coordinate plane.
You don’t have an equation for m(x) here, but no problem—this question is still solvable. Start by determining whether m(x) has an inverse. By performing the horizontal line test, you should quickly see that m(x) passes the test and, therefore, has an inverse. (Refer to the graph on the left below.)
Now that you know m−1(x) exists, you need to draw it. Draw the line of reflection, reflect m(x) across the line of reflection, and sketch the graph of m−1(x). Alternatively, pick some points on m(x) and reverse the x- and y-values. For example, m(x) includes the points {(−3, −5), (−2, −3), (−1, −1), (0, 1), (1, 3)}, so m−1(x) includes the points {(−5, −3), (−3, −2), (−1, −1), (1, 0), (3, 1)}. Regardless of the method you use, the graph of m−1(x) should resemble the lighter line in the figure on the right.
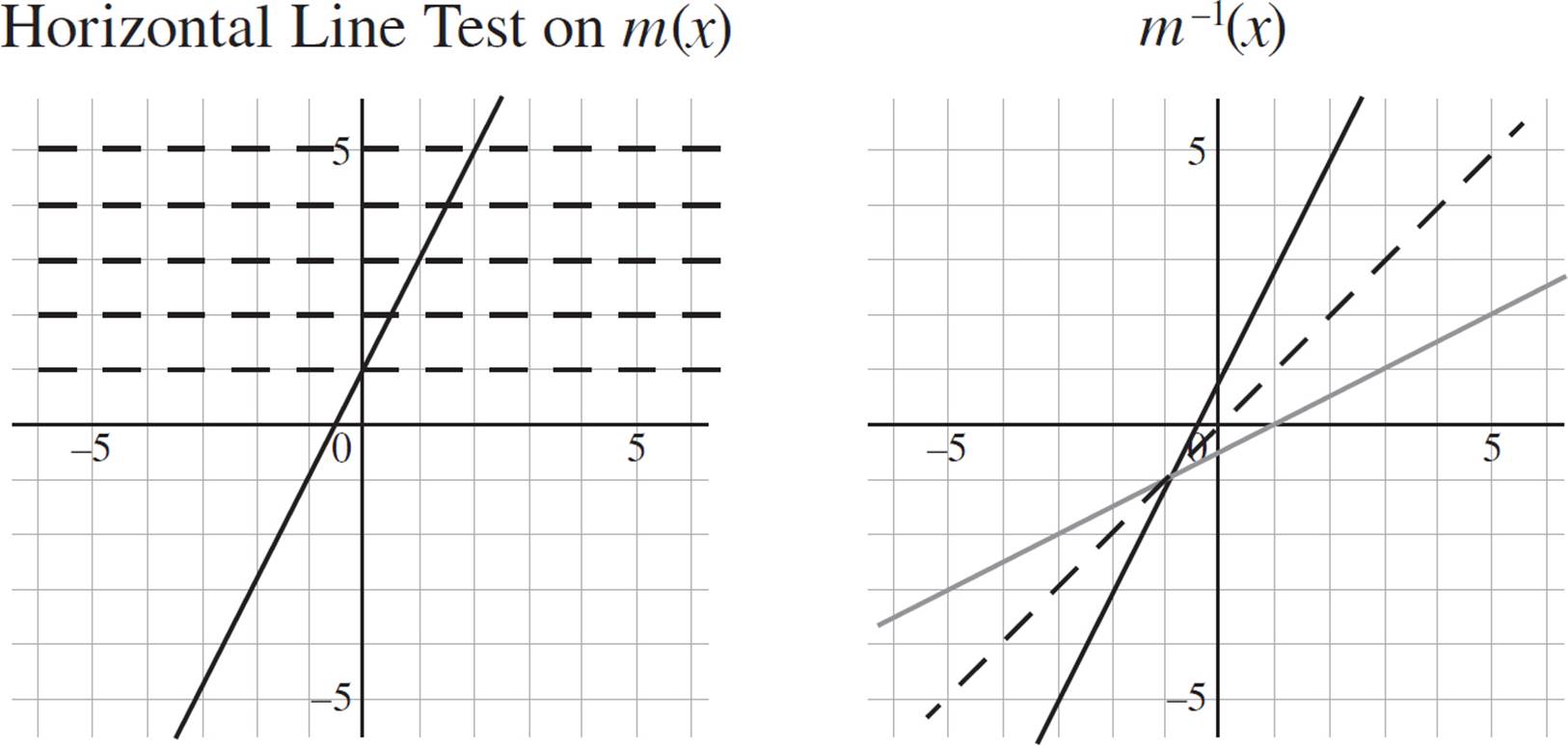
And that is all there is to it! You successfully graphed the inverse of m(x) without even knowing the value of the function.

You’re on a roll! Let’s try one more question.
EXAMPLE 
Given the function d(x) = (x + 2)3 + 4, find d−1(x).
In order to answer this question, you need to know the process for finding the inverse of a function. The first step in solving for d−1(x) is to replace d(x) with y in the original function.
d(x) = (x + 2)3 + 4
y = (x + 2)3 + 4
Next, switch x and y in the equation.
y = (x + 2)3 + 4
x = (y + 2)3 + 4
Then solve for y:
x = (y + 2)3 + 4
x − 4 = (y + 2)3![]() = y + 2
= y + 2 ![]() − 2 = y
− 2 = y
Finally, replace the y with d−1(x).
d−1(x) = ![]() − 2
− 2
And there you have it You’ve successfully found the inverse equation of d(x).

Nice job! You should now be familiar with the more complex functions that will be introduced in Algebra I. Now test and reinforce your skills by tackling the end-of-chapter questions.
DRILL
CHAPTER 10 PRACTICE QUESTIONS
Click here to download a PDF of Chapter 10 Practice Questions.
Directions: Complete the following problems as specified by each question. For extra practice, try using an alternative method to solve the problem or check your work.
Questions 1−3 refer to the following function n(x).
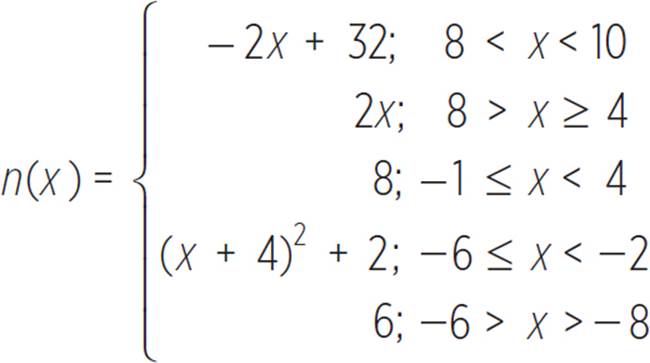
1. a. Graph n(x) in the coordinate plane.
b. State whether the function is continuous or discontinuous.
c. State whether the function is an absolute value, piecewise, or step function.
2. Identify n(−2), n(0), and n(2).
3. Determine the domain and range of n(x).
4. Graph zoltan(x) = ![]() (x − 4)2 + 2 and state whether the function has an inverse.
(x − 4)2 + 2 and state whether the function has an inverse.
Questions 5−7 refer to the function f(x) = 2![]() .
.
5. Graph f(x) and state whether the function has an inverse.
6. Determine f−1(x) algebraically.
7. Graph f−1(x) in the coordinate plane.
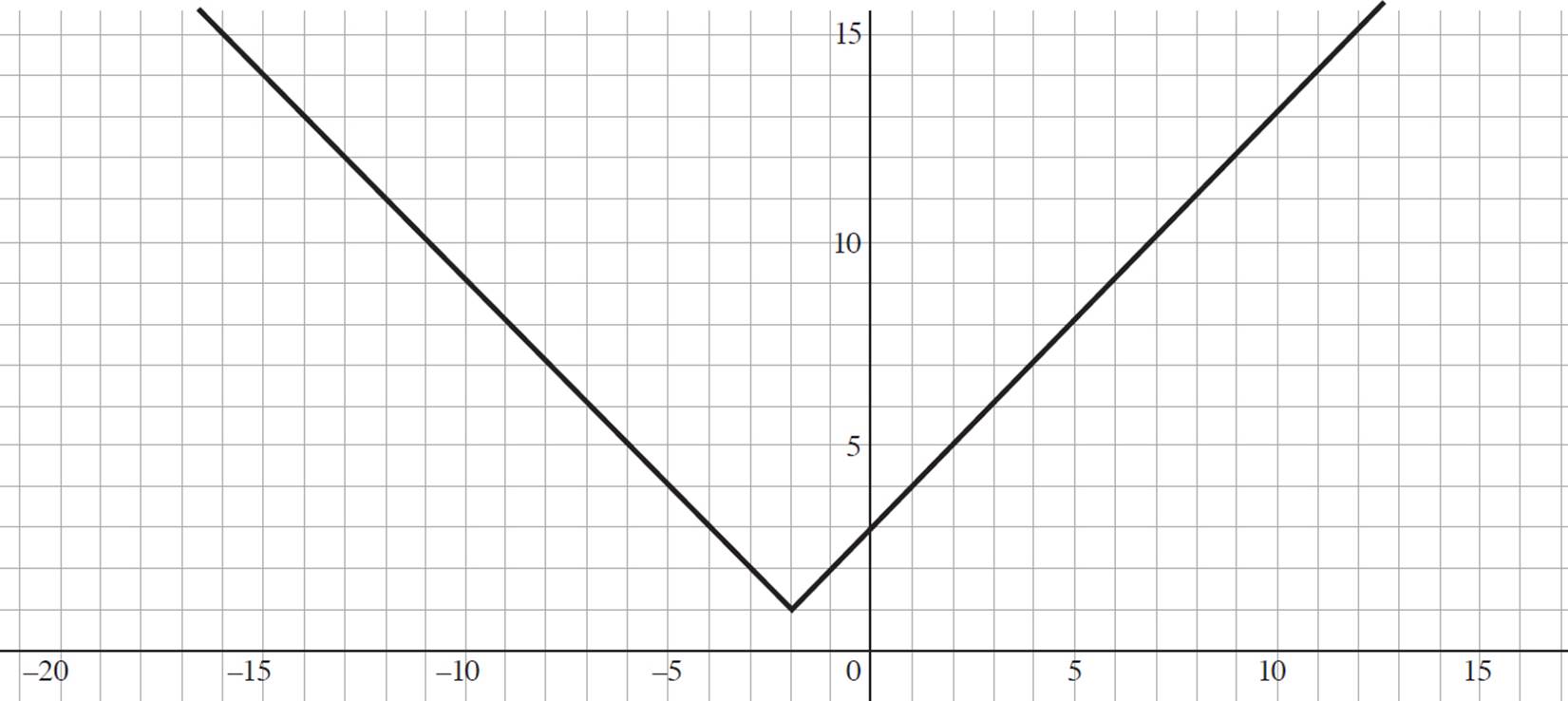
8. Given the graph of the function sofia(x) = |x + 2| + 1 above and fabien(x) = 2[sofia(x)] − 1, graph the function in the coordinate plane and determine the value of fabien(3).
Questions 9−10 refer to the function goo(x), shown below.
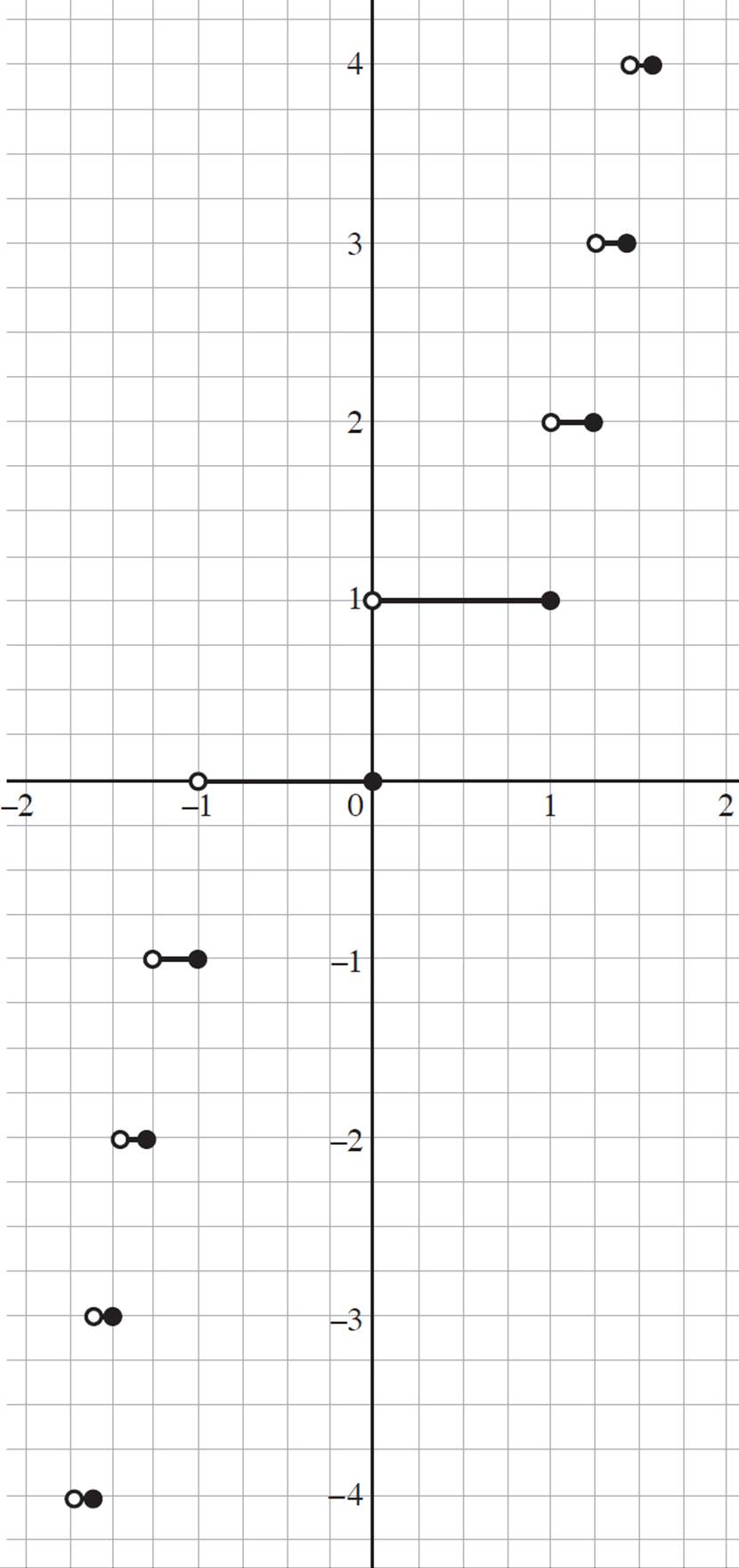
9. Given the graph of goo(x), do the following:
a. State whether the function is continuous or discontinuous.
b. State whether the function is an absolute value, piecewise, or step function.
c. If the function is a step function, state whether the function is a floor or ceiling function.
10. Determine the values of goo(−1.1), goo(0), and goo(1.1).
SOLUTIONS TO CHAPTER 10 PRACTICE QUESTIONS
1. Discontinuous; Piecewise
You’re told that n(x) = −2x + 32 when 8 < x < 10, n(x) = 2x when 8 > x ³ 4, n(x) = 8 when −1 ≤ x < 4, n(x) = (x + 4)2 when −6 ≤ x < −2, and n(x) = 6 when −6 > x > −8.
Start by graphing each piece of the function in turn, according to the conditions of the function; thus, this is a piecewise function. Plot each piece of the function as you would any other function, taking care to follow the restrictions placed on each piece of n(x). The resulting graph should resemble the following.
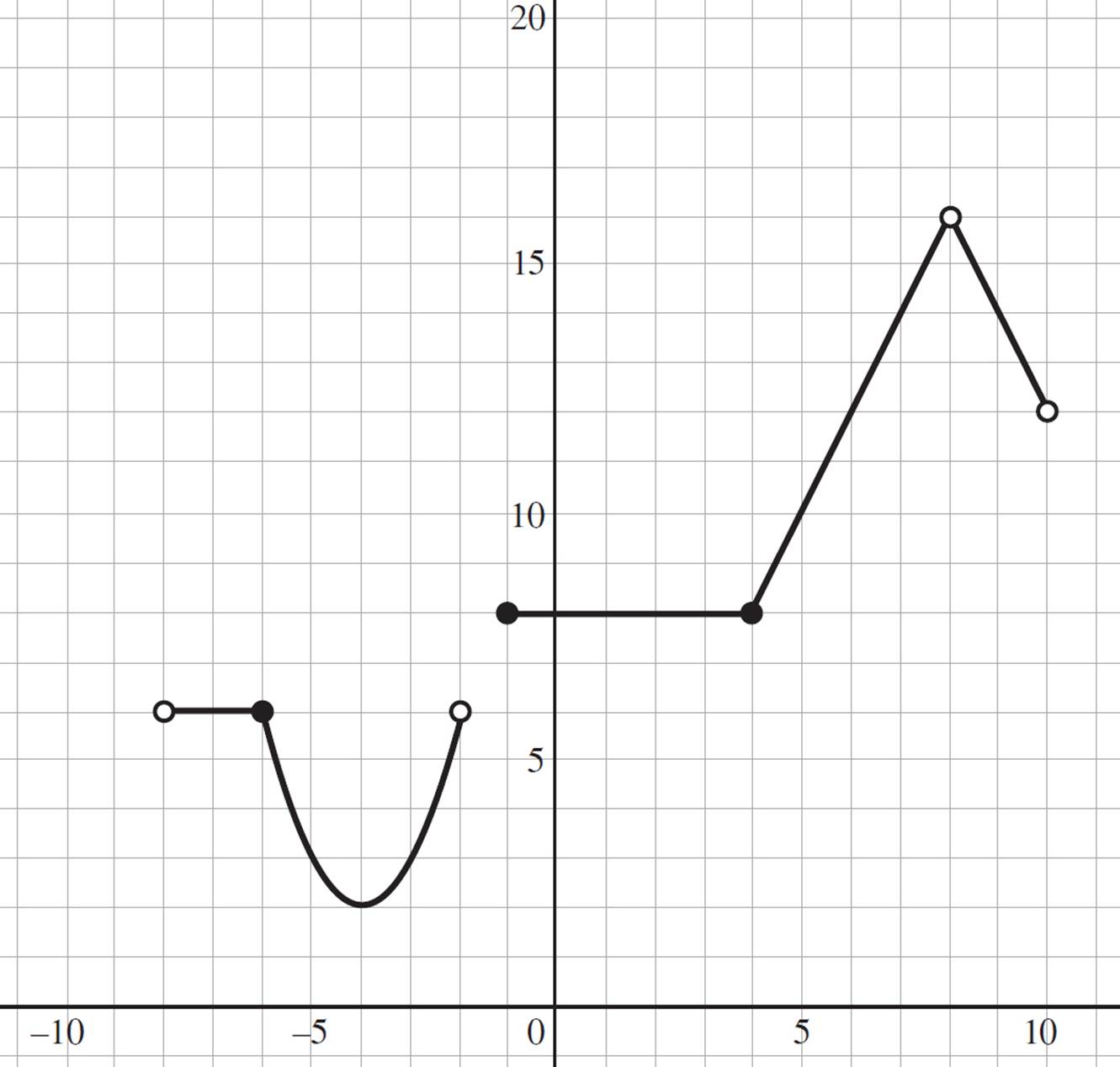
This question also requires you to determine if the function is continuous or discontinuous. If you look at the graph, the answer should be evident: There are multiple breaks and holes in the function, so the function is discontinuous. The question further requires you to determine whether it is an absolute value, piecewise, or step function. Since the function is given in multiple pieces without any absolute value or ceiling or floor, this is a piecewise function.
2. n(−2) does not exist; n(0) = 8; n(2) = 8
This question requires you to use the graph from the previous question to determine n(−2), n(0), and n(2). To find the value of n(−2), find the y-value when x = −2 on the graph; when x = −2 on n(x), there is an open circle, indicating a gap in the function. Therefore, n(−2) does not exist on the function. Now, find n(0). Based on the graph, when x = 0, y = 8. Thus, n(0) = 8. Finally, repeat the process to find n(2). According to the graph, when x = 2, y = 8. So, n(2) = 8.
3. Domain: (−8, −2) ∪ [−1, 8) ∪ (8, 10); Range: [2, 6] ∪ [8, 16)
Here you’re asked to determine the domain and range of n(x) in interval notation. First, you need to find the domain. Because of the discontinuities at (−8, 6), (−2, 6), and (8, 16), as well as the gap between x = −2 and x = −1, the domain cannot be expressed as a single interval. Rather, you will need to express the domain as the union (∪) of multiple intervals. Here, the domain of d(x) in interval notation is (−8, −2) ∪ [−1, 8) ∪ (8, 10). Finally, determine the range of d(x), taking into account the discontinuity that occurs at (8, 16), and the gap that exists between y = 6 and y = 8. Therefore, the range of the function is expressed as [2, 6] ∪ [8, 16).
4. The function does not have an inverse.
For this question, you need to graph zoltan(x) = 1/2(x − 4)2 + 2 and determine whether the relation is a function. Start by graphing the function as you would any normal function. Since zoltan(x) = 1/2(x − 4)2 + 2 is already in vertex form, where f(x) = (x − h)2 + kand (h, k) is the vertex, you know that the vertex of this function is at (4, 2).
Next, find the y-intercept by setting x = 0 and solving for y:
y = 1/2(x − 4)2 + 2
y = 1/2(0 − 4)2 + 2
y = 1/2(16) + 2
y = 8 + 2
y = 10
Therefore, the y-intercept is (0, 10). Now find the roots by setting y = 0 and solving for x:
y = 1/2(x − 4)2 + 2
0 = 1/2(x − 4)2 + 2
= 1/2(x − 4)2 = −2
(x − 4)2 = −4
(x − 4) = ![]()
x = 4 ± ![]()
The square root of a negative number doesn’t result in any real solutions; and since zoltan(x) does not have any real solutions, there are no x-intercepts to this function. However, now that you know the vertex and the y-intercept of zoltan(x), you can graph the function as follows.
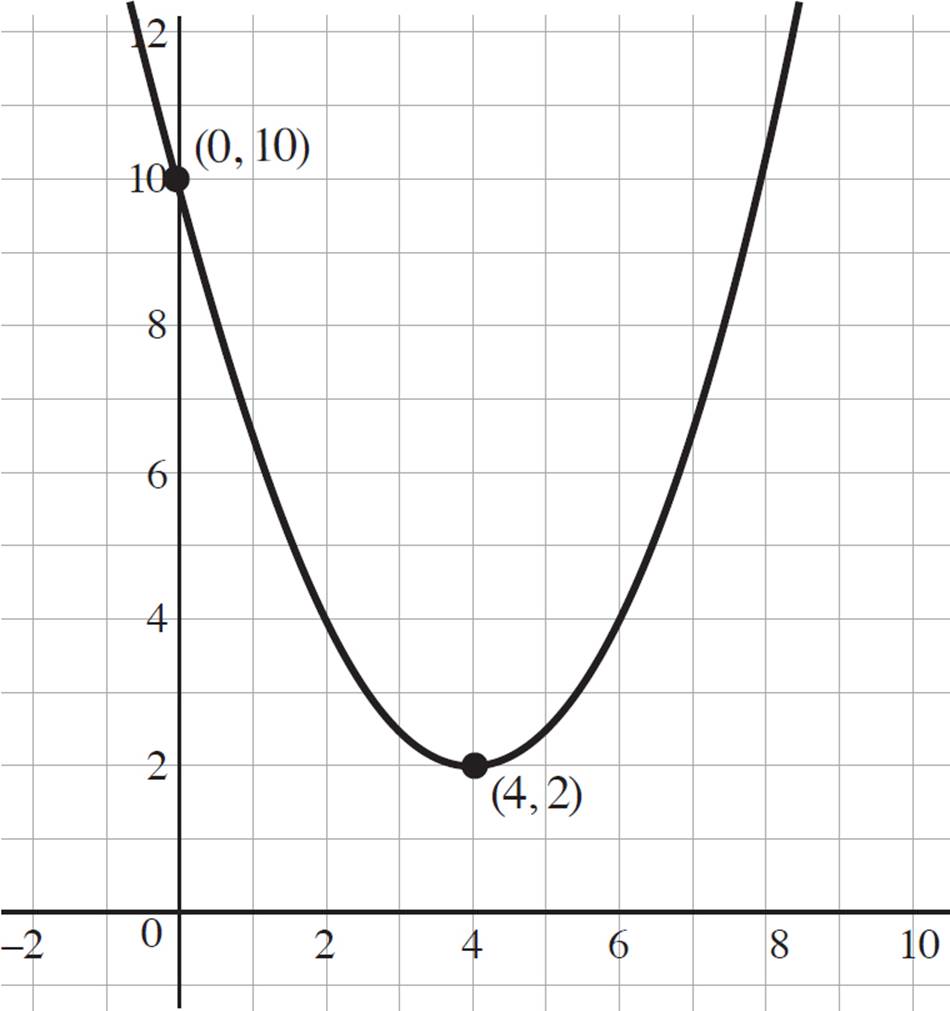
Finally, you need to determine whether zoltan(x) has an inverse. Since the function is a quadratic and fails the horizontal line test, the function does not have an inverse.
5. The function has an inverse.
Here you need to use the information provided to graph f(x) = 2![]() in the coordinate plane, and then state whether the function has an inverse. To graph this function, start by finding the x- and y-intercepts. To find the x-intercept, set y = 0 and then solve for x:
in the coordinate plane, and then state whether the function has an inverse. To graph this function, start by finding the x- and y-intercepts. To find the x-intercept, set y = 0 and then solve for x:
f(x) = 2![]()
2![]() = 0
= 0
8(x + 4) = 0
8x + 32 = 0
8x = −32
x = −4
Thus, the x-intercept is (−4, 0). Now find the y-intercept by setting x = 0, and solving for y, or f(x):
f(x) = 2![]()
y = 2![]()
y = 2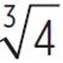
y = 2(1.59)
y = 3.18
Thus, the y-intercept is at (0, 3.175). You should also find a few other plot points before graphing f(x). Try finding f(4):
f(x) = 2![]()
f(4) = 2![]()
f(4) = 2![]()
f(4) = 2(2)
f(4) = 4
Therefore, the point (4, 4) is part of the function. Now try finding f(−2):
f(x) = 2![]()
f(−2) = 2![]()
f(−2) = 2![]()
f(−2) = 2(1.26)
f(−2) = 4.52
Let’s find one more point that occurs below the x-axis:
f(x) = 2![]()
f(−7) = 2![]()
f(−7) = ![]()
f(−7) = 2(1.44)
f(−7) = 2.88
The point (−2, 4.52) is also part of the function. Now that you have some plot points, graph the function, which will look quite similar to the graph of ![]() .
.
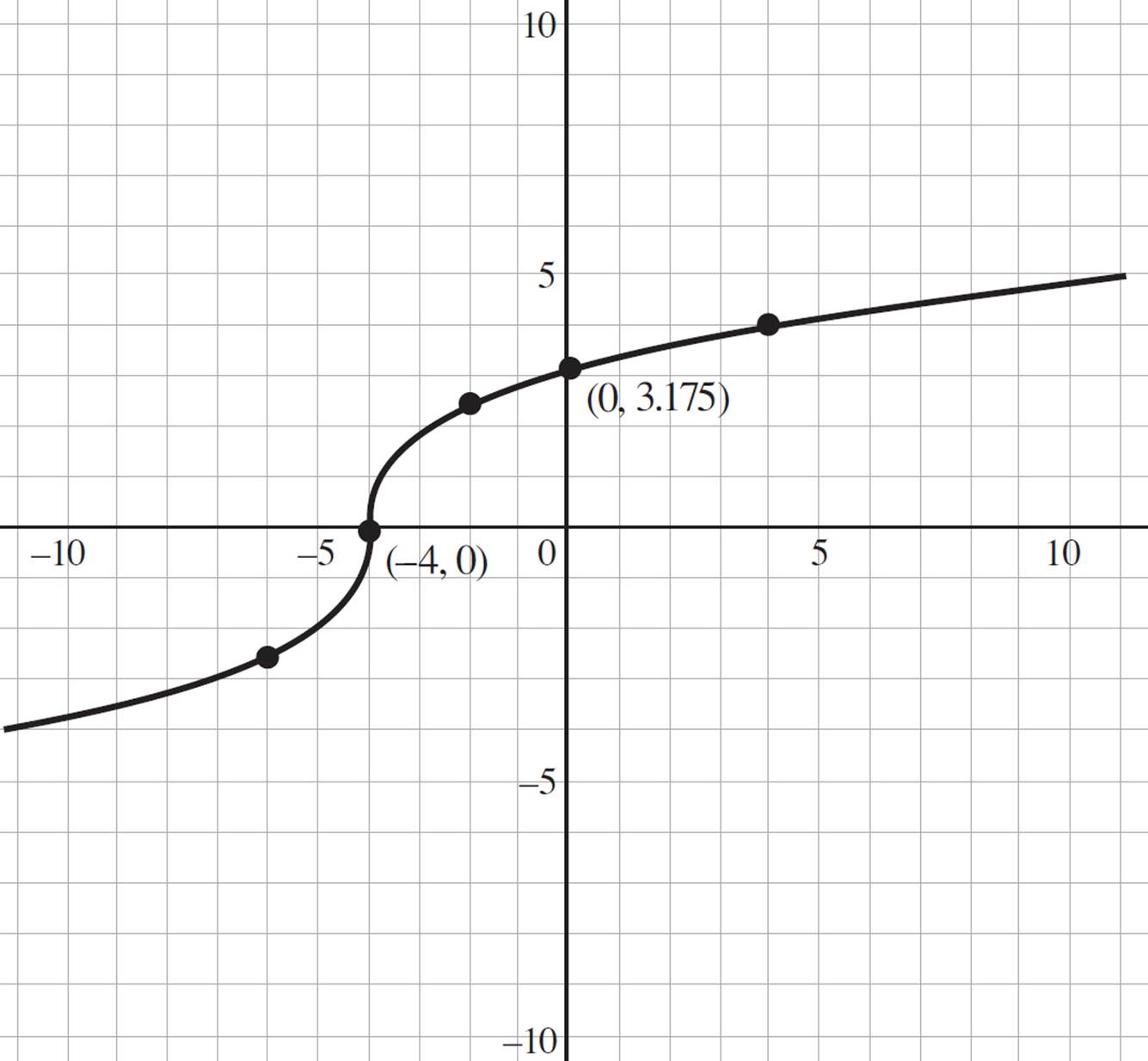
Now that the function f(x) is graphed, determine if the function has an inverse. Conduct the horizontal line test on f(x). Here, the function passes the horizontal line test and, therefore, f(x) has an inverse.
6. f−1(x) = ![]() − 4
− 4
This question builds upon the previous question and requires you to determine f−1(x), given that f(x) = 2![]() , algebraically. The first step in solving for f−1(x) is to replace f(x) with y in the original function: f(x) = 2
, algebraically. The first step in solving for f−1(x) is to replace f(x) with y in the original function: f(x) = 2![]() becomes y = 2
becomes y = 2![]() . Next, switch x and yin the equation: y = 2
. Next, switch x and yin the equation: y = 2![]() becomes x = 2
becomes x = 2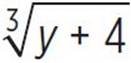 . Then, solve for y:
. Then, solve for y:
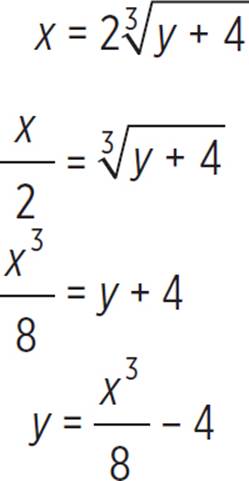
Finally, replace the y with f−1(x): y = ![]() − 4 becomes f−1(x) =
− 4 becomes f−1(x) = ![]() − 4.
− 4.
7. Now that you’ve graphed the original function f(x) and defined f−1(x), you now have to graph f−1(x). In question 5, you found the x- and y-intercepts of f(x) are (−4, 0) and (0, 3.175), respectively. Since f−1(x) is the inverse of f(x), you know that the x- and y-intercepts of f−1(x) are (3.175, 0) and (0, −4). Plot these points and draw the line of reflection on your graph. See the graph below.
Once you have the x- and y-intercepts of f−1(x) and the reflection line graphed, you can use the graph to identify other points that lie on f−1(x). Based on the graph, you will find that the original function, f(x), contains the points (− 8, −3.175), (−5, −2), (4, 4), and (10, 4.82). Therefore, the inverse function, f−1(x), contains the points (−3.175, −8), (−2, −5), (4, 4), and (4.82, 10). You can then plot these points and then graph f−1(x) as shown by the dashed line in the graph below.
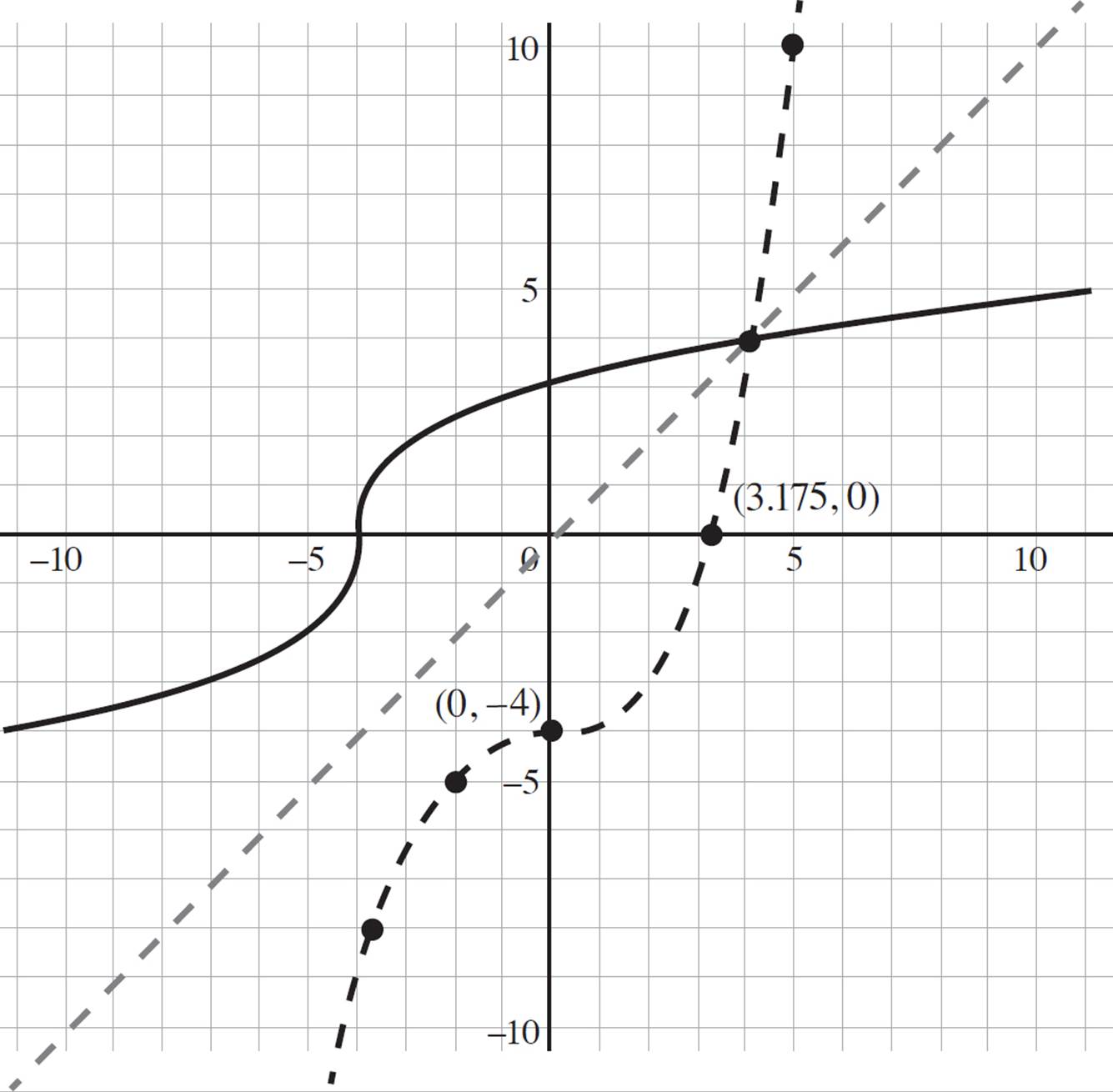
8. fabien(3) = 11
You are given the graph of the function sofia(x) = |x + 2| + 1, told that fabien(x) = 2[sofia(x)] − 1, and required graph the function and determine fabien(3). To do this, you need to understand how fabien(x) is transformed from the original function, sofia(x).
First, determine the function fabien(x). If you were to expand fabien(x), you will find that
fabien(x) = 2[sofia(x)] − 1
fabien(x) = 2[|x + 2| + 1] − 1
fabien(x) = |2x + 4| + 2 − 1
fabien(x) = |2x + 4| + 1
Since the function can be put into vertex form, in which f(x) = a|x − h| + k and (h, k) is the vertex to get f(x) = 2|x + 2| + 1, the vertex of fabien(x) is (−2, 1).
Now consider the 2 in the function fabien(x) = |2x + 4| + 1. Recall that for any function, if a > 1, the image will have a vertical stretch in the y-direction appearing taller and thinner than the pre-image, sofia(x). Since fabien(x) = |2x + 4| + 1, the value of a is 2, and the graph of the function will be vertically stretched by a factor of 2, indicating that the vertex of fabien(x) will be (−2, 2).
You may also want to find a few points to plot for the function fabien(x) = |2x + 4| + 1. First, find the y-intercept by setting x = 0 and solving for y:
fabien(x) = |2x + 4| + 1
fabien(0) = |2(0) + 4| + 1
fabien(0) = |4| + 1
fabien(0) = 5
Thus, the y-intercept is (0, 5). If we set x = 1, we find that
fabien(x) = |2x + 4| + 1
fabien(1) = |2(1) + 4| + 1
fabien(1) = |6| + 1
fabien(1) = 7
Therefore, point (1, 7) exists on the function. Similarly, if we set x = −1, we find that
fabien(x) = |2x + 4| + 1
fabien(−1) = |2(−1) + 4| + 1
fabien(−1) = |2| + 1
fabien(−1) = 3
Thus, the point (−1, 3) exists on the function. Finally, plot the vertex (−2, 1), the y-intercept (0, 5), and the points (1, 7) and (−1, 3), and graph fabien(x) as shown:
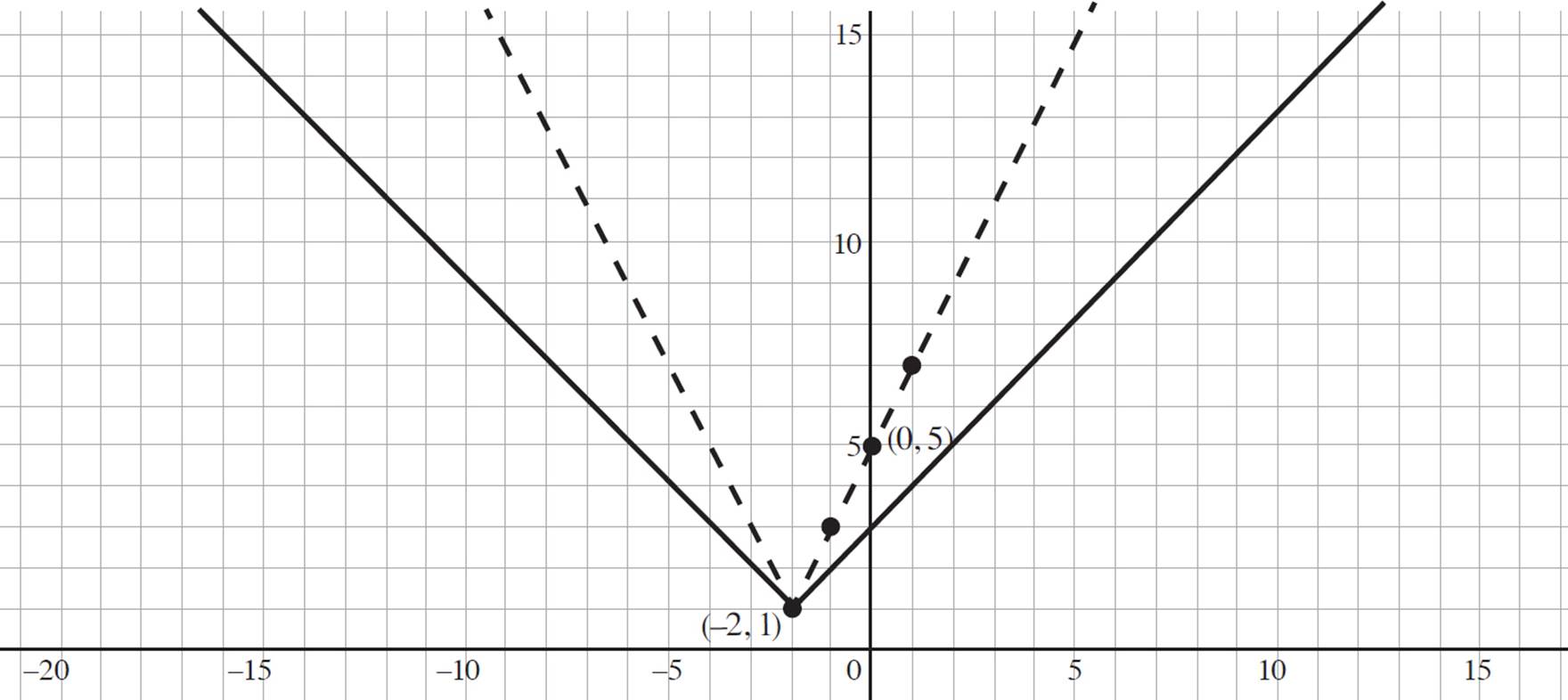
The last part of the question requires you to determine fabien(3). Look at the graph of fabien(x) and find the y-value that exists when x = 3. Here, fabien(3) = 11.
9. Discontinuous; Step function; Ceiling function
Start by determining whether the function is continuous or discontinuous. Because there are numerous breaks and gaps in the graph of the function, the function is discontinuous.
Now determine if goo(x) is an absolute value, piecewise, or step function. Since the function does not depict a V-shaped image, the function is not an absolute value function. A step function is related to a piecewise function but consists of constant horizontal pieces occurring at adjacent intervals of the function; the graph of a step function looks like a set of steps, or a staircase. So, while the function could be classified as a piecewise function, the function is more precisely classified as a step function.
Finally, you need to determine whether the step function is a floor function or a ceiling function. A floor function returns the greatest integer that is less than or equal to x, while a ceiling function returns the least integer that is greater than or equal to x. Consider a value of goo(x). For example, goo(−0.4) = 0 and goo(0.4) = 1, indicating that the function returns a value greater than x. Thus, goo(x) is a ceiling function.
10. goo(−1.1) = −1; goo(0) = 0; goo(1.1) = 2
Here, you need to use the graph of goo(x) to determine the value of goo(−1.1), goo(0), and goo(1.1). Since goo(x) is a ceiling function, the function returns the least integer that is greater than or equal to x. Let’s start with goo(−1.1); since a ceiling function returns the least integer greater than or equal to x, the value of jgoo(−1.1) = −1.
Now tackle goo(0); in any step function, the value of an integer is the integer itself. Therefore, goo(0) = 0.
Finally, determine goo(1.1). Again, since a ceiling function returns the least integer greater than or equal to x, the value of goo(1.1) = 2.
REFLECT
Congratulations on completing Chapter 10!
Here’s what we just covered.
Rate your confidence in your ability to:
•Identify absolute value, step, and piecewise functions
1 2 3 4 5
•Graph and manipulate absolute value, step, and piecewise functions
1 2 3 4 5
•Determine whether a function is continuous or discontinuous
1 2 3 4 5
•Determine, identify, and graph inverse functions
1 2 3 4 5
•Explain the purpose of the horizontal line test
1 2 3 4 5
If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.
CHAPTER 10 KEY POINTS
![]() The absolute value function is graphed as a symmetrical “V” shape. Since the absolute value is the distance from zero, the basic graph f(x) = |x| has a domain of all real numbers, but a range of all positive numbers.
The absolute value function is graphed as a symmetrical “V” shape. Since the absolute value is the distance from zero, the basic graph f(x) = |x| has a domain of all real numbers, but a range of all positive numbers.
![]() A piecewise function is a function that is comprised of at least two equations, or pieces, that are applied to different parts of the domain.
A piecewise function is a function that is comprised of at least two equations, or pieces, that are applied to different parts of the domain.
![]() Piecewise functions do not all have to be of the same form; for example, it is possible that the “pieces” can all be quadratic functions, or it is possible that the pieces are a combination of constant, linear, quadratic, cubic, exponential, or absolute value functions.
Piecewise functions do not all have to be of the same form; for example, it is possible that the “pieces” can all be quadratic functions, or it is possible that the pieces are a combination of constant, linear, quadratic, cubic, exponential, or absolute value functions.
![]() Piecewise functions can be continuous, having no breaks or holes in the function, or discontinuous, having breaks or holes in the function.
Piecewise functions can be continuous, having no breaks or holes in the function, or discontinuous, having breaks or holes in the function.
![]() Piecewise functions will have graphs that have open or closed dots on the ends.
Piecewise functions will have graphs that have open or closed dots on the ends.
○ A closed, or solid, dot indicates that the value is included in the piece of the function.
○ An open, or unfilled, dot indicates that the value is not included in the piece of the function.
![]() A step function is a piecewise function in the form f(x) = [x] that consists of constant horizontal pieces occurring at adjacent intervals of the function. When graphed, the function ends up looking like a set of steps, or a staircase.
A step function is a piecewise function in the form f(x) = [x] that consists of constant horizontal pieces occurring at adjacent intervals of the function. When graphed, the function ends up looking like a set of steps, or a staircase.
○ Step functions can be classified as floor or ceiling functions.
○ A floor function, denoted as floor[x], returns the greatest integer that is less than or equal to x.
○ A ceiling function, denoted as ceil[x], returns the least integer that is greater than or equal to x.
![]() The horizontal line test is used to determine whether every y-value in a function has only one, unique x-value. If a function f(x) has more than one x-value for a single y-value, it has failed the horizontal line test, and you can conclude that the function f(x) does not have an inverse.
The horizontal line test is used to determine whether every y-value in a function has only one, unique x-value. If a function f(x) has more than one x-value for a single y-value, it has failed the horizontal line test, and you can conclude that the function f(x) does not have an inverse.
![]() The process for solving for f−1(x) given f(x) is as follows:
The process for solving for f−1(x) given f(x) is as follows:
○ Step 1: Given a function, replace the term f(x) with y.
○ Step 2: Switch the x- and y-terms.
○ Step 3: Solve for y.
○ Step 4: Replace y with f−1(x).