Calculus For Dummies, 2nd Edition (2014)

Part IV. Differentiation

Chapter 12. Your Problems Are Solved: Differentiation to the Rescue!

IN THIS CHAPTER

Getting the most bang for your buck — optimization problems

Position, velocity, and acceleration — VROOOOM

Related rates — brace yourself

In the Introduction, I argue that calculus has changed the world in countless ways, that its impact is not limited to Ivory Tower mathematics, but is all around us in down-to-earth things like microwave ovens, cell phones, and cars. Well, it’s now Chapter 12, and I’m finally ready to show you how to use calculus to solve some practical problems.

Getting the Most (or Least) Out of Life: Optimization Problems

One of the most practical uses of differentiation is finding the maximum or minimum value of a real-world function: the maximum output of a factory, the maximum strength of a beam, the minimum time to accomplish some task, the maximum range of a missile, and so on. Let’s get started with a couple standard geometry examples.

The maximum volume of a box

A box with no top is to be manufactured from a 30-inch-by-30-inch piece of cardboard by cutting and folding it, as shown in Figure 12-1.

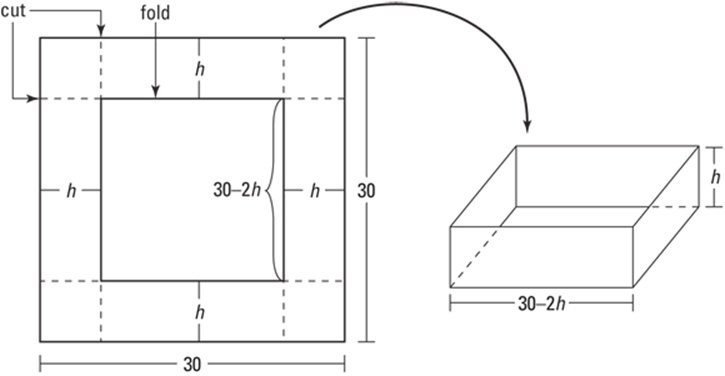
FIGURE 12-1: The box is made from a 30"-by-30" piece of cardboard by cutting off the corners and folding up the sides.

What dimensions will produce a box with the maximum volume? Mathematics often seems abstract and impractical, but here’s an honest-to-goodness practical problem (well … almost). If a manufacturer can sell bigger boxes for more and is making 100,000 boxes, you’d better believe he or she wants the exact answer to this question. Here’s how you do it:

1. Express the thing you want maximized, the volume, as a function of the unknown, the height of the box (which is the same as the length of the cut).

2. Determine the domain of your function.

The height can’t be negative, and because the length (and width) of the box equals , which can’t be negative, h can’t be greater than 15. Thus, sensible values for h are . You now want to find the maximum value of in this interval. You use the method from the “Finding Absolute Extrema on a Closed Interval” section in Chapter 11.

3. Find the critical numbers of in the open interval by setting its derivative equal to zero and solving. And don’t forget to check for numbers where the derivative is undefined.

Because 15 is not in the open interval , it doesn’t qualify as a critical number (though this is a moot point because you end up testing it in Step 4 anyway). And because this derivative is defined for all input values and is, thus, of course, never undefined, there are no additional critical numbers. So 5 is the only critical number.

4. Evaluate the function at the critical number, 5, and at the endpoints of the interval, 0 and 15, to locate the function’s max.

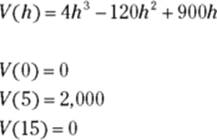
Test the endpoints. The extremum (dig that fancy word for maximum or minimum) you’re looking for doesn’t often occur at an endpoint, but it can — so don’t fail to evaluate the function at the interval’s two endpoints.

So, a height of 5 inches produces the box with maximum volume (2,000 cubic inches). Because the length and width equal , a height of 5 gives a length and width of , or 20, and thus the dimensions of the desired box are . That’s it.

The maximum area of a corral — yeehaw!

A rancher can afford 300 feet of fencing to build a corral that’s divided into two equal rectangles. See Figure 12-2.

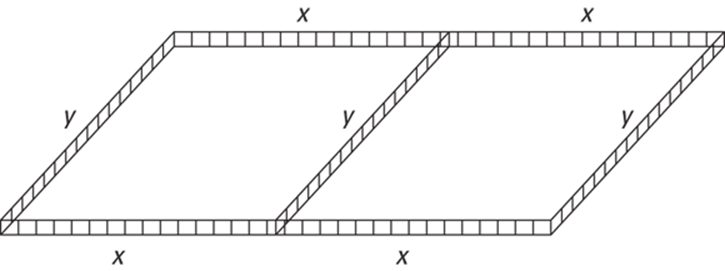
FIGURE 12-2: Calculus for cowboys — maximizing a corral.

What dimensions will maximize the corral’s area? This is another practical problem. The rancher wants to give his animals as much room as possible given the length of fencing he can afford. Like all businesspeople, he wants the most bang for his buck.

1.a. Express the thing you want maximized (area) as a function of the two unknowns (x and y).

In the cardboard box example in the previous section, you can easily write the volume as a function of one variable — which is always what you need. But here, the area is a function of two variables (x and y), so Step 1 has the following two extra sub-steps that will eliminate one of the variables.

1.b. Use the given information to relate the two variables to each other.

The 300 feet of fencing is used for seven sections, thus

1.c. Solve this equation for y and plug the result in for y in the equation from Step 1.a. This gives you what you need — a function of one variable.

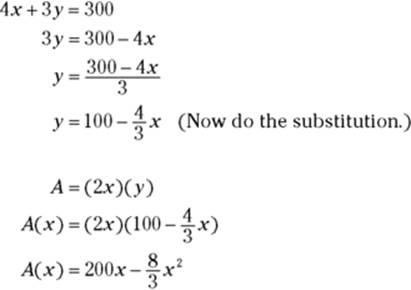
2. Determine the domain of the function.

You can’t have a negative length of fence, so x can’t be negative, and the most x can be is 300 divided by 4, or 75. Thus, .

3. Find the critical numbers of in the open interval by setting its derivative equal to zero and solving (and check whether the derivative is undefined anywhere in the interval).

Because is defined for all x-values, 37.5 is the only critical number.

4. Evaluate the function at the critical number, 37.5, and at the endpoints of the interval, 0 and 75.

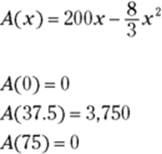
Note: Evaluating a function at the endpoints of a closed interval is a standard step in finding an absolute extremum on the interval. However, you could have skipped this step here had you noticed that is an upside-down parabola and that, therefore, its peak at must be higher than either endpoint.

The maximum value in the interval is 3,750, and thus, an x-value of 37.5 feet maximizes the corral’s area. The length is 2x, or 75 feet. The width is y, which equals . Plugging in 37.5 gives you , or 50 feet. So the rancher will build a 75'  ×   50' corral with an area of 3,750 square feet.

Yo-Yo a Go-Go: Position, Velocity, and Acceleration

Every time you get in your car, you witness differentiation. Your speed is the first derivative of your position. And when you step on the accelerator or the brake — accelerating or decelerating — you experience a second derivative.

The derivative of position is velocity, and the derivative of velocity is acceleration. If a function gives the position of something as a function of time, you differentiate the position function to get the velocityfunction, and you differentiate the velocity function to get the acceleration function. Stated a different but equivalent way, the first derivative of position is velocity, and the second derivative of position is acceleration.

Here’s an example. A yo-yo moves straight up and down. Its height above the ground, as a function of time, is given by the function , where t is in seconds and is in inches. At , it’s 30 inches above the ground, and after 4 seconds, it’s at a height of 18 inches. See Figure 12-3.

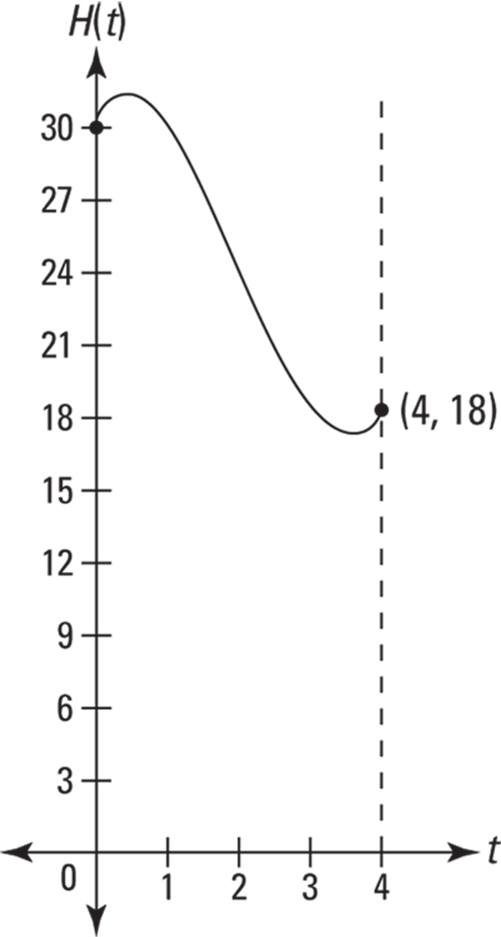
FIGURE 12-3: The yo-yo’s height, from 0 to 4 seconds.

Velocity, , is the derivative of position (height, in this problem), and acceleration, , is the derivative of velocity. Thus:

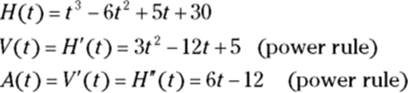
Take a look at the graphs of these three functions in Figure 12-4.

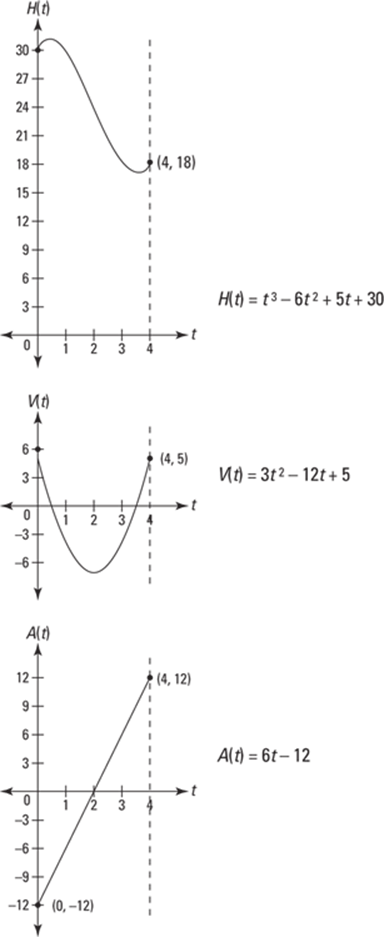
FIGURE 12-4: The graphs of the yo-yo’s height, velocity, and acceleration functions from 0 to 4 seconds.

Using the three functions and their graphs, I want to discuss several things about the yo-yo’s motion:

· Maximum and minimum height

· Maximum, minimum, and average velocity

· Total displacement

· Maximum, minimum, and average speed

· Total distance traveled

· Positive and negative acceleration

· Speeding up and slowing down

Because this is a lot to cover, I’ll cut some corners — like not always checking endpoints when looking for extrema if it’s obvious that they don’t occur at the endpoints. Do you mind? I didn’t think so. (Position, velocity, and acceleration problems make use of several ideas from Chapter 11 — local extrema, concavity, inflection points — so you may want to take a look back at those definitions if you’re a little hazy.) But before tackling the bulleted topics, let’s go over a few things about velocity, speed, and, acceleration.

Velocity, speed, and acceleration

None of your friends will complain — or even notice — if you use the words “velocity” and “speed” interchangeably, but your friendly mathematician will complain. Here’s the difference. For the velocity function in Figure 12-4, upward motion by the yo-yo is defined as a positive velocity, and downward motion is a negative velocity. This is the standard way velocity is treated in most calculus and physics problems. (Or, if the motion is horizontal, going right is a positive velocity and going left is a negative velocity.)

Speed, on the other hand, is always positive (or zero). If a car goes by at 50 mph, for instance, you say its speed is 50, and you mean positive 50, regardless of whether it’s going to the right or the left. For velocity, the direction matters; for speed, it does not. In everyday life, speed is a simpler idea than velocity because it’s always positive and because it agrees with our commonsense notion about how fast something is moving. But in calculus, speed is actually the trickier idea because it doesn’t fit nicely into the three-function scheme shown in Figure 12-4.

You’ve got to keep the velocity-speed distinction in mind when analyzing velocity and acceleration. The way we talk about velocity, speed, and acceleration — in calculus class, as opposed to in everyday life — can get pretty weird. For example, if an object is going down (or to the left) faster and faster, its speed is increasing, but its velocity is decreasing because its velocity is becoming a bigger and bigger negative (and bigger negatives are smaller numbers). This seems weird, but that’s the way it works. And here’s another strange thing: Acceleration is defined as the rate of change of velocity, not speed. So, if an object is slowing down while going in the downward direction and thus has an increasing velocity — because the velocity is becoming a smaller and smaller negative — the object has a positive acceleration. In everyday English, you’d say that the object is decelerating (slowing down), but in calculus class, though you could still say the object is slowing down, you’d say that the object has a negative velocity and a positive acceleration. (By the way, decelerationisn’t exactly a technical term, so you should probably avoid it in calculus class. It’s best to use the following vocabulary: positive acceleration, negative acceleration, positive velocity, negative velocity, speeding up, and slowing down.) I could go on with this stuff, but I bet you’ve had enough.

Maximum and minimum height

The maximum and minimum height of the yo-yo, in other words, the max and min of , occur at the local extrema you can see in Figure 12-4. To locate them, set the derivative of (that’s ) equal to zero and solve:

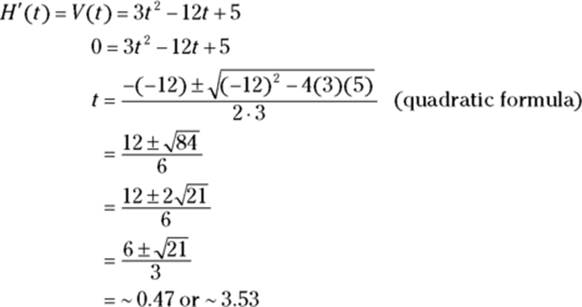
These two numbers are the zeros of (which is ) and the t-coordinates, that’s time-coordinates, of the max and min of , which you can see in Figure 12-4. In other words, these are the times when the yo-yo reaches its maximum and minimum heights. Plug these numbers into to obtain the heights:

So the yo-yo gets as high as about 31.1 inches above the ground at seconds and as low as about 16.9 inches at seconds. (By the way, do you see why the max and min of the yo-yo’s height would occur when the yo-yo’s velocity is zero?)

Velocity and displacement

As I explain in the “Velocity versus speed” section, velocity is basically like speed except that while speed is always positive (or zero), velocity can be positive (when going up or to the right) or negative (when going down or to the left). The connection between displacement and distance traveled is similar: Distance traveled is always positive (or zero), but going down (or left) counts as negative displacement. In everyday speech, speed and distance traveled are the more user-friendly ideas, but when it comes to calculus and physics, velocity and displacement are the more fundamental ideas.

Total displacement

Let’s get back to our yo-yo analysis. Total displacement is defined as final position minus initial position. So, because the yo-yo starts at a height of 30 and ends at a height of 18,

This is negative because the net movement is downward.

Average velocity

Average velocity is given by total displacement divided by elapsed time. We just calculated the total distance , and time runs from 0 seconds to 4 seconds, so the elapsed time is 4 seconds. Thus,

This answer of negative 3 tells you that the yo-yo is, on average, going down 3 inches per second.

Maximum and minimum velocity

To determine the yo-yo’s maximum and minimum velocity during the interval from 0 to 4 seconds, set the derivative of (that’s ) equal to zero and solve:

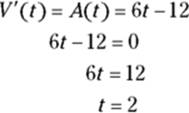
(Look again at Figure 12-4. At , you get the zero of , the local min of , and the inflection point of . But you already knew that, right? If not, check out Chapter 11.)

Now, evaluate , at the critical number, 2, and at the interval’s endpoints, 0 and 4:

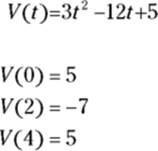
So, the yo-yo has a maximum velocity of 5 inches per second twice — at both the beginning and the end of the interval. It reaches a minimum velocity of inches per second at seconds.

Speed and distance traveled

As mentioned in the previous section, velocity and displacement are the more technical concepts, while speed and distance traveled are the more commonsense ideas. Speed, of course, is the thing you read on your speedometer, and you can read distance traveled on your odometer or your “tripometer” after setting it to zero.

Total distance traveled

To determine total distance, add up the distances traveled on each leg of the yo-yo’s trip: the up leg, the down leg, and the second up leg.

First, the yo-yo goes up from a height of 30 inches to about 31.1 inches (where the first turn-around point is). That’s a distance of about 1.1 inches. Next, it goes down from about 31.1 to about 16.9 (the height of the second turn-around point). That’s a distance of 31.1 minus 16.9, or about 14.2 inches. Finally, the yo-yo goes up again from about 16.9 inches to its final height of 18 inches. That’s another 1.1 inches. Add these three distances to obtain the total distance traveled: . (Note: Compare this answer to the total displacement of . The displacement is negative because the net movement is downward. And the positive amount of the displacement (namely 12) is less than the distance traveled of 16.4 because with displacement the up legs of the yo-yo’s trip cancel out part of the down leg distance. Check out the math: . Get it?)

Average speed

The yo-yo’s average speed is given by the total distance traveled divided by the elapsed time. Thus,

Maximum and minimum speed

You previously determined the yo-yo’s maximum velocity (5 inches per second) and its minimum velocity ( inches per second). A velocity of is a speed of 7, so that’s the yo-yo’s maximum speed. Its minimum speed of zero occurs at the two turnaround points.

A good way to analyze maximum and minimum speed is to consider the speed function and its graph. (Or, if you’re a glutton for punishment, check out the mumbo jumbo below.) Speed equals the absolute value of velocity. So, for our yo-yo problem, the speed function, , equals . Check out the graph of in Figure 12-5. Looking at this graph, it’s easy to see that the yo-yo’s maximum speed occurs at (the maximum speed is ) and that the minimum speed is zero at the two x-intercepts.

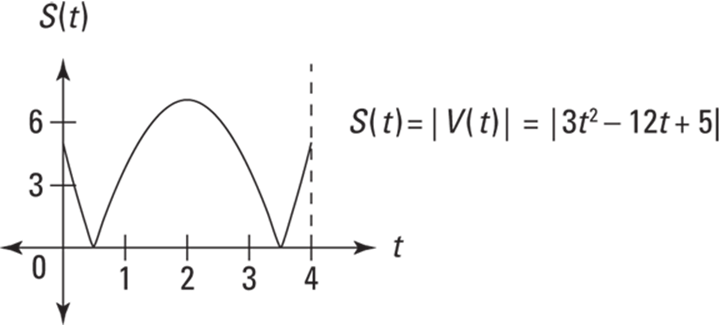
FIGURE 12-5: The yo-yo’s speed function, .

Minimum and maximum speed: For a continuous velocity function, the minimum speed is zero whenever the maximum and minimum velocities are of opposite signs or when one of them is zero. When the maximum and minimum velocities are both positive or both negative, then the minimum speed is the lesser of the absolute values of the maximum and minimum velocities. In all cases, the maximum speed is the greater of the absolute values of the maximum and minimum velocities. Is that a mouthful or what?

Burning some rubber with acceleration

Let’s go over acceleration: Put your pedal to the metal.

Positive and negative acceleration

The graph of the acceleration function at the bottom of Figure 12-4 is a simple line, . It’s easy to see that the acceleration of the yo-yo goes from a minimum of at seconds to a maximum of at seconds, and that the acceleration is zero at when the yo-yo reaches its minimum velocity (and maximum speed). When the acceleration is negative — on the interval — that means that the velocity is decreasing. When the acceleration is positive — on the interval — the velocity is increasing.

Speeding up and slowing down

Figuring out when the yo-yo is speeding up and slowing down is probably more interesting and descriptive of its motion than the info in the preceding section. An object is speeding up (what we call “acceleration” in everyday speech) whenever the velocity and the calculus acceleration are both positive or both negative. And an object is slowing down (“deceleration” in everyday speech) when the velocity and the calculus acceleration are of opposite signs.

Look at all three graphs in Figure 12-4 again. From to about , the velocity is positive and the acceleration is negative, so the yo-yo is slowing down while moving upward (till its velocity becomes zero and it reaches its maximum height). In plain English, the yo-yo is decelerating from 0 to about 0.47 seconds. The greatest deceleration occurs at when the deceleration is (the graph shows negative 12, but I’m calling it positive 12 because I’m calling it a deceleration, get it?)

From about to , both velocity and acceleration are negative, so the yo-yo is speeding up while moving downward. From to about , velocity is negative and acceleration is positive, so the yo-yo is slowing down again as it continues downward (till it bottoms out at its lowest height). Finally, from about to , both velocity and acceleration are positive, so the yo-yo is speeding up again. The yo-yo reaches its greatest acceleration of at seconds.

WHAT THE HECK IS A SECOND SQUARED?

Note that I use the unit for acceleration instead of the equivalent but weird-looking unit, . You often see acceleration given in terms of a unit of distance over or you might see something like . But what the heck is a ? It’s meaningless, and something like is a bad way to think about acceleration. The best way to understand acceleration is as a change in speed per unit of time. If a car can go from 0 to 60 mph in 6 seconds, that’s an increase in speed of 60 mph in 6 seconds, or, on average, 10 mph each second — that’s an acceleration of .

It’s slightly more confusing when the speed has a unit like feet/second and the unit of time for the acceleration is also a second, because then the word second appears twice. But it still works like the car example. Say an object starts at rest and speeds up to 10 feet/second after 1 second, then up to 20 feet/second after 2 seconds, to 30 feet/second after 3 seconds, and so on. Its speed is increasing 10 feet/second each second, and that’s an acceleration of or . (By the way, it’s helpful to write the acceleration unit in either of these ways (using a vertical fraction) as a speed over the unit of time — instead of horizontally like 10 feet per second per second or 10 feet/second/second — to emphasize that acceleration is a change in speed per unit of time.) Think of acceleration this way, not in terms of that nonsense.

Tying it all together

Note the following connections among the three graphs in Figure 12-4. The negative section on the graph of — from to — corresponds to a decreasing section of the graph of and a concave down section of the graph of . The positive interval on the graph of — from to — corresponds to an increasing interval on the graph of and a concave up interval on the graph of . When seconds, has a zero, has a local minimum, and has an inflection point.

Related Rates — They Rate, Relatively

Say you’re filling up your swimming pool and you know how fast water is coming out of your hose, and you want to calculate how fast the water level in the pool is rising. You know one rate (how fast the water is being poured in), and you want to determine another rate (how fast the water level is rising). These rates are called related rates because one depends on the other — the faster the water is poured in, the faster the water level will rise. In a typical related rates problem (like the one just described), the rate or rates in the given information are constant, unchanging, and you have to figure out a related rate that is changing with time. You have to determine this related rate at one particular point in time. (If this isn’t crystal clear, you’ll see what I mean in a minute when you work through the following problems.)

Solving these problems can be tricky at first, but with practice you’ll get the hang of it. The strategies and tips are a big help — let’s do three examples.

Blowing up a balloon

You’re blowing up a balloon at a rate of 300 cubic inches per minute. When the balloon’s radius is 3 inches, how fast is the radius increasing?

1. Draw a diagram, labeling it with any unchanging measurements (there aren’t any in this unusually simple problem) and making sure to assign a variable to anything in the problem that’s changing (unless it’s irrelevant to the problem). See Figure 12-6.

Notice that the radius in Figure 12-6 is labeled with the variable r. The radius needs a variable because as the balloon is being blown up, the radius is changing. I put the 3 in parentheses to emphasize that the number 3 is notan unchanging measurement. The problem asks you to determine something when the radius is 3 inches, but remember, the radius is constantly changing.

Changing or unchanging? In related rates problems, it’s important to distinguish between what is changing and what is not changing.

The volume of the balloon is also changing, so you need a variable for volume, V. You could put a V on your diagram to indicate the changing volume, but there’s really no easy way to mark part of the balloon with a V like you can show the radius with an r.

2. List the given rate and the rate you’re asked to determine as derivatives with respect to time.

You’re pumping up the balloon at 300 cubic inches per minute. That’s a rate — a change in volume (cubic inches) per change in time (minutes). So,

cubic inches per minute

You have to figure out a related rate, namely, how fast the radius is changing, so

3. Write down the formula that connects the variables in the problem, V and r.

Here’s the formula for the volume of a sphere:

4. Differentiate your formula with respect to time, t.

When you differentiate in a related rates problem, all variables are treated like the ys are treated in a typical implicit differentiation problem.

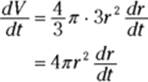
You need to add the just like the way you add on a or a with implicit differentiation.

5. Substitute known values for the rate and variables in the equation from Step 4, and then solve for the thing you’re asked to determine.

It’s given that , and you’re asked to figure out when so plug in these numbers and solve for .

Differentiate before you plug in. Be sure to differentiate (Step 4) before you plug the given information into the unknowns (Step 5).

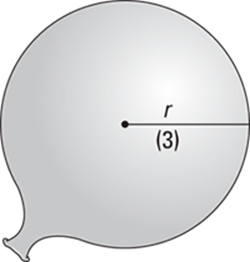
FIGURE 12-6: Blowing up a balloon — time to party!

So the radius is increasing at a rate of about 2.65 inches per minute when the radius measures 3 inches. Think of all the balloons you’ve blown up since your childhood. Now you finally have the answer to the question that’s been bugging you all these years.

By the way, if you plug 5 into r instead of 3, you get an answer of about 0.95 inches per minute. This should agree with your balloon-blowing-up experience: The bigger the balloon gets, the slower it grows. It’s a good idea to check things like this every so often to see that the math agrees with common sense.

Filling up a trough

Here’s another related rates problem. A trough is being filled up with swill. The trough is 10 feet long, and its cross-section is an isosceles triangle with a base of 2 feet and a height of 2 feet 6 inches (with the vertex at the bottom, of course). Swill’s being poured in at a rate of 5 cubic feet per minute. When the depth of the swill is 1 foot 3 inches, how fast is the swill level rising?

1. Draw a diagram, labeling it with any unchanging measurements and assigning variables to any changing things. See Figure 12-7.

Note that Figure 12-7 shows the unchanging dimensions of the trough, 2 feet, 2 feet 6 inches, and 10 feet, and that these dimensions do not have variable names like l for length or h for height. And note that the changing things — the height (or depth) of the swill and the width of the surface of the swill (which gets wider as the swill gets deeper) — have variable names, h for height and b for base (I say base instead of width because it’s the base of the upside-down triangle shape made by the swill). The volume of the swill is also changing, so you can call that V.

2. List the given rate and the rate you’re asked to figure out as derivatives with respect to time.

3.a. Write down the formula that connects the variables in the problem: V, h, and b.

I’m absolutely positive that you remember the formula for the volume of a right prism (the shape of the swill in the trough):

Note that this “base” is the base of the prism (the whole triangle at the end of the trough), not the base of the triangle which is labeled b in Figure 12-6. Also, this “height” is the height of the prism (the length of the trough), not the height labeled h in Figure 12-7. Sorry about the confusion. Deal with it.

The area of the triangular base equals , and the “height” of the prism is 10 feet, so the formula becomes

Now, unlike the formula in the balloon example, this formula contains a variable, b, that you don’t see in your list of derivatives in Step 2. So Step 3 has a second part — getting rid of this extra variable.

3.b. Find an equation that relates the unwanted variable, b, to some other variable in the problem so you can make a substitution that leaves you with only V and h.

The triangular face of the swill in the trough is similar to the triangular face of the trough itself, so the base and height of these triangles are proportional. (Recall from geometry that similar triangles are triangles of the same shape; their sides are proportional.) Thus,

Be on the lookout for similar triangles. Similar triangles come up a lot in related rates problems. Look for them whenever the problem involves a triangle, a triangular prism, or a cone shape.

Now substitute 0.8h for b in your formula from Step 3.a.

4. Differentiate this equation with respect to t.

5. Substitute known values for the rate and variable in the equation from Step 4 and then solve.

You know that cubic feet per minute, and you want to determine when h equals 1 foot 3 inches, or 1.25 feet, so plug in 5 and 1.25 and solve for :

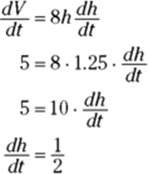
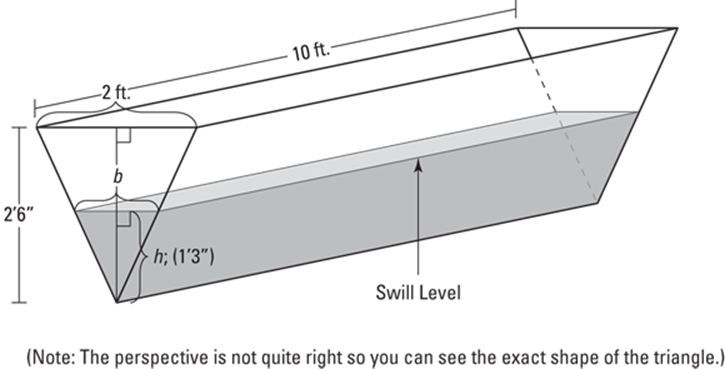
FIGURE 12-7: Filling a trough with swill — lunch time.

That’s it. The swill’s level is rising at a rate of foot per minute when the swill is 1 foot 3 inches deep. Dig in.

Fasten your seat belt: You’re approaching a calculus crossroads

Ready for another common related rates problem? One car leaves an intersection traveling north at 50 mph, another is driving west toward the intersection at 40 mph. At one point, the north-bound car is three-tenths of a mile north of the intersection, and the west-bound car is four-tenths of a mile east of it. At this point, how fast is the distance between the cars changing?

1. Do the diagram thing. See Figure 12-8.

Variable or fixed? Before going on with this problem, I want to mention a similar problem you may run across if you’re using a standard calculus textbook. It involves a ladder leaning against and sliding down a wall. Can you see that the diagram for such a ladder problem would be very similar to Figure 12-8 except that the y-axis would represent the wall, the x-axis would be the ground, and the diagonal line would be the ladder? These problems are quite similar, but there’s an important difference. The distance between the cars is changing so the diagonal line in Figure 12-8 is labeled with a variable, s. A ladder, on the other hand, has a fixed length, so the diagonal line in your diagram for the ladder problem would be labeled with a number, not a variable.

2. List all given rates and the unknown rate.

As Car A travels north, the distance y is growing at 50 miles per hour. That’s a rate, a change in distance per change in time. So,

As Car B travels west, the distance x is shrinking at 40 miles per hour. That’s a negative rate:

You have to figure out how fast s is changing, so,

3. Write the formula that relates the variables in the problem: x, y, and s.

The Pythagorean theorem, , will do the trick for this right triangle problem. In this problem, x and y are the legs of the right triangle, and s is the hypotenuse, so .

The Pythagorean theorem is used a lot in related rates problems. If there’s a right triangle in your problem, it’s quite likely that is the formula you’ll need.

Because this formula contains the variables x, y, and s which all appear in your list of derivatives in Step 2, you don’t have to tweak this formula like you did in the trough problem.

4. Differentiate with respect to t.

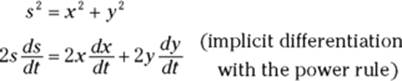
(Remember, in a related rates problem, all variables are treated like the ys in an implicit differentiation problem.)

5. Substitute and solve for .

“Holy devoid distance lacking length, Batman. How can we solve for unless we have values for the rest of the unknowns in the equation?” “Take a chill pill, Robin — just use the Pythagorean theorem again.”

You can reject the negative answer because s obviously has a positive length. So .

Now plug everything into your equation:

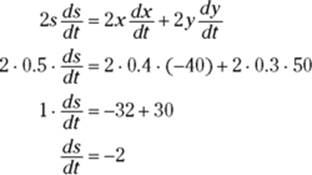
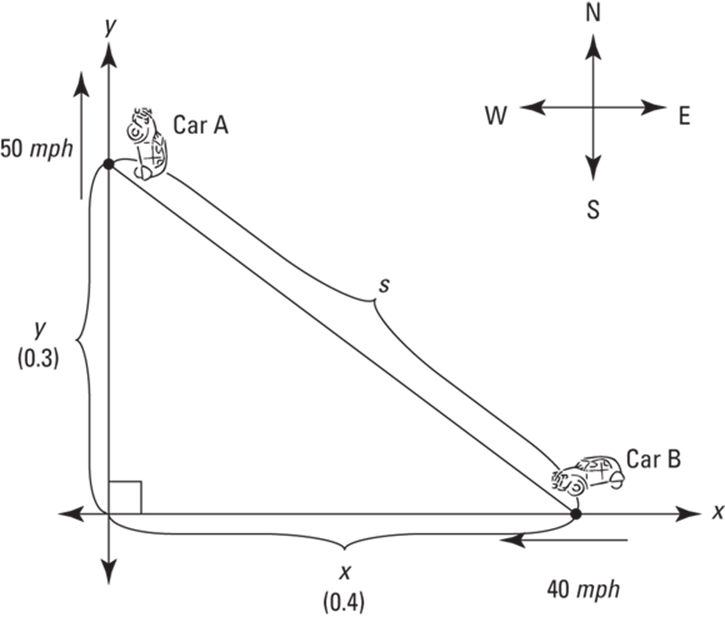
FIGURE 12-8: Calculus — it’s a drive in the country.

This negative answer means that the distance, s, is decreasing.

Thus, when car A is 3 blocks north of the intersection and car B is 4 blocks east of it, the distance between them is decreasing at a rate of 2 mph.